
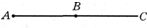 如图所示,B为直线AC的中点,质点甲从A点由静止出发做匀加速运动,到达B点时的速度为v,则它到达C点时的速度大小为$\sqrt{2}v$;若质点乙也从A点由静止出发,在AC间做简谐运动,到达B点时的速度也为v,则甲、乙从A点到B点所用的时间之比为$\sqrt{2}$:1.
如图所示,B为直线AC的中点,质点甲从A点由静止出发做匀加速运动,到达B点时的速度为v,则它到达C点时的速度大小为$\sqrt{2}v$;若质点乙也从A点由静止出发,在AC间做简谐运动,到达B点时的速度也为v,则甲、乙从A点到B点所用的时间之比为$\sqrt{2}$:1. 分析 由速度-位移公式即可求出质点甲从A到达C的速度;抓住末速度相等,位移相同,根据速度时间图线比较甲乙运动的时间.
解答 解:质点甲做匀加速直线运动,到达B点时:2ax=v2-0
到达C点时:$2a•2x={v}_{c}^{2}-0$
所以:${v}_{c}=\sqrt{2}v$
质点甲做匀加速直线运动,平均速度:$\overline{v}=\frac{0+v}{2}$
质点乙做简谐振动,从A到B的过程中做加速度减小的加速运动,根据运动的特点可知其速度表达式为:vt=vmsinωt
所以在$\frac{1}{4}$周期内的平均速度为:$\overline{v}′=\frac{\sqrt{2}}{2}{v}_{m}=\frac{\sqrt{2}}{2}v$
两种运动的位移相等,所以它们使用的时间的比:
$\frac{{t}_{1}}{{t}_{2}}=\frac{\overline{v}′}{\overline{v}}=\frac{\frac{\sqrt{2}}{2}v}{\frac{1}{2}v}=\frac{\sqrt{2}}{1}$
故答案为:$\sqrt{2}v$,$\sqrt{2}$:1
点评 解决本题的关键掌握速度时间图线的特点,知道图线的斜率表示加速度,图线与时间轴所围成的面积表示位移.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中物理 来源: 题型:多选题
| A. | 月球的质量与地球的质量之比$\frac{{{G}_{1}{R}_{2}}^{2}}{{{{G}_{2}R}_{1}}^{2}}$ | |
| B. | 月球表面处的重力加速度g月为$\frac{{G}_{2}}{{G}_{1}}$g | |
| C. | 月球的第一宇宙速度与地球的第一宇宙速度之比为$\sqrt{\frac{{G}_{1}{R}_{2}}{{G}_{2}{R}_{1}}}$ | |
| D. | 卫星在距月球表面轨道上做匀速圆周运动的周期T月为2π$\sqrt{\frac{{R}_{2}{G}_{1}}{{gG}_{2}}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
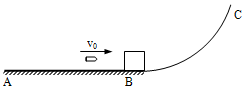 水平轨道AB,在B点处与半径R=100m的光滑弧形轨道BC相切,一个质量为M=1.0kg的木块以v0=1m/s的水平速度从B点冲上弧形轨道,如图所示.已知木块与该水平轨道AB的动摩擦因数μ=0.5(g取10m/s2).试求:
水平轨道AB,在B点处与半径R=100m的光滑弧形轨道BC相切,一个质量为M=1.0kg的木块以v0=1m/s的水平速度从B点冲上弧形轨道,如图所示.已知木块与该水平轨道AB的动摩擦因数μ=0.5(g取10m/s2).试求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 只要物体做平滑的曲线运动,它在任意一段时间内的动量变化一定不为零 | |
| B. | 某一段时间内物体受的冲量不为零,它的动量可能不变化 | |
| C. | 做曲线运动的物体,它的动量对时间的变化率一定为零 | |
| D. | 某一时刻物体的动量为零,它的动量时间的变化率可能不为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
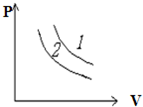 如图所示,质量分别为m1和m2的同种气体,分别以恒定的温度t1和t2等温变化,变化过程分别用图中等温线1和2表示,如m1=m2,则t1>t2;如t1=t2,m1>m2.(填“>”“=”或“<”)
如图所示,质量分别为m1和m2的同种气体,分别以恒定的温度t1和t2等温变化,变化过程分别用图中等温线1和2表示,如m1=m2,则t1>t2;如t1=t2,m1>m2.(填“>”“=”或“<”)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
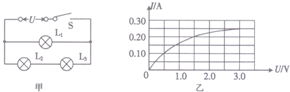 在如图甲所示的电路中,电源电动势为3.0V,L1、L2、L3为3个相同规格的小灯泡,这种小灯泡的伏安特性曲线如图乙所示.则当开关闭合后电路稳定时( )
在如图甲所示的电路中,电源电动势为3.0V,L1、L2、L3为3个相同规格的小灯泡,这种小灯泡的伏安特性曲线如图乙所示.则当开关闭合后电路稳定时( )| A. | L1电流为通过L2电流的2倍 | B. | L1的电阻为15Ω | ||
| C. | L2两端的电压为3.0V | D. | L2的电阻为7.5Ω |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 月球的半径为$\frac{s}{θ}$ | |
| B. | 月球的质量为$\frac{{s}^{3}}{Gθ{t}^{2}}$ | |
| C. | 月球的密度为$\frac{3{θ}^{2}}{4πG{t}^{2}}$ | |
| D. | 若该卫星距月球表面的高度变大,其绕月球运动的线速度变大 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
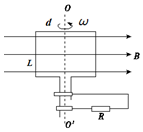 如图所示,匀强磁场磁感应强度B=0.5T,发电机转子的矩形线圈长L=0.5m,宽d=0.4m,匝数n=10匝,以角速度ω=20πrad/s绕OO'轴匀速转动.当线圈转到图示位置时,线圈产生感应电动势值为62.8V;当线圈由图示位置转过60°时,线圈产生的感应电动势值为31.4V.
如图所示,匀强磁场磁感应强度B=0.5T,发电机转子的矩形线圈长L=0.5m,宽d=0.4m,匝数n=10匝,以角速度ω=20πrad/s绕OO'轴匀速转动.当线圈转到图示位置时,线圈产生感应电动势值为62.8V;当线圈由图示位置转过60°时,线圈产生的感应电动势值为31.4V.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com