
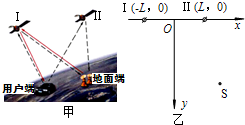
 北斗卫星导航系统是我国正在自主研发的全球卫星导航系统,该系统由空间端(卫星)、地面端(中心控制系统)和用户端(导航定位仪)三部分组成,预计2020年形成全球覆盖能力.目前正在试用的“北斗一号”卫星导航试验系统也称“双星定位导航系统”,利用两颗地球同步静止轨道卫星为用户提供快速定位导航服务.
北斗卫星导航系统是我国正在自主研发的全球卫星导航系统,该系统由空间端(卫星)、地面端(中心控制系统)和用户端(导航定位仪)三部分组成,预计2020年形成全球覆盖能力.目前正在试用的“北斗一号”卫星导航试验系统也称“双星定位导航系统”,利用两颗地球同步静止轨道卫星为用户提供快速定位导航服务.分析 (1)根据万有引力提供向心力,由万有引力定律和牛顿运动定律列出等式求解.
(2)根据题意及几何关系求出用户S的坐标关系.
解答 解:(1)设地球的质量为M,“北斗一号”卫星的质量为m,其轨道高度为h,根据牛顿第二定律和万有引力定律得:
$G\frac{Mm}{(R+h)^{2}}=m\frac{4{π}^{2}(R+h)}{{T}^{2}}$
对地面上质量为m0的物体有:$\frac{GM{m}_{0}}{{R}^{2}}={m}_{0}g$
联立上述二式,可解得:h=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}-R$
(2)①设用户S的坐标为(x,y),根据题意及几何关系,有:
$(x+L)^{2}+(y-0)^{2}=(c{t}_{1})^{2}$
${(x-L)}^{2}+{(y-0)}^{2}={(c{t}_{2})}^{2}$
解得S的位置坐标为($\frac{{c}^{2}({{t}_{1}}^{2}-{{t}_{2}}^{2})}{4L}$,$\sqrt{{c}^{2}{{t}_{1}}^{2}-[\frac{{c}^{2}({{t}_{1}}^{2}-{{t}_{2}}^{2})}{4L}+L]^{2}}$)
②实际导航定位过程中,为了确定用户在空间中的位置,还需要测出并提供用户所在位置的高度.
答:(1)“北斗一号”同步静止轨道卫星距地面的高度为$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}-R$;
(2)①用户S在此平面内的位置坐标为($\frac{{c}^{2}({{t}_{1}}^{2}-{{t}_{2}}^{2})}{4L}$,$\sqrt{{c}^{2}{{t}_{1}}^{2}-[\frac{{c}^{2}({{t}_{1}}^{2}-{{t}_{2}}^{2})}{4L}+L]^{2}}$).
②实际导航定位过程中,为了确定用户在空间中的位置,还需要测出并提供用户所在位置的高度.
点评 地球质量一定、自转速度一定,同步卫星要与地球的自转实现同步,就必须要角速度与地球自转角速度相等,这就决定了它的轨道高度和线速度大小.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
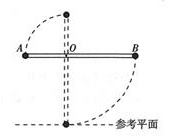 如图所示,长为3r的轻杆(轻杆的质量忽略不计)两端各固定一质量为m的小球A和B.在轻杆上安装一水平光滑轴O.A球距水平轴O的距离为r.对B球施加一作用力,使轻杆处于水平位置.现撤去作用力,轻杆开始自由转动,当轻杆转到竖直位置时,求:
如图所示,长为3r的轻杆(轻杆的质量忽略不计)两端各固定一质量为m的小球A和B.在轻杆上安装一水平光滑轴O.A球距水平轴O的距离为r.对B球施加一作用力,使轻杆处于水平位置.现撤去作用力,轻杆开始自由转动,当轻杆转到竖直位置时,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,直杆长L1=0.5m,圆筒高为L2=3.7m.直杆位于 圆筒正上方H=0.8m处.直杆从静止开始做自由落体运动,并能竖直穿越圆筒.(取g=10m/s2),试求:
如图所示,直杆长L1=0.5m,圆筒高为L2=3.7m.直杆位于 圆筒正上方H=0.8m处.直杆从静止开始做自由落体运动,并能竖直穿越圆筒.(取g=10m/s2),试求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示的电路中,A、B间电压恒为3.2V,3个电阻的阻值均为4Ω,电容器的电容为30 μF,电流表为理想电流表.那么电路稳定时电容器所带的电量、电流表的读数分别是( )
如图所示的电路中,A、B间电压恒为3.2V,3个电阻的阻值均为4Ω,电容器的电容为30 μF,电流表为理想电流表.那么电路稳定时电容器所带的电量、电流表的读数分别是( )| A. | 9.6×10-5 C,0.8 A | B. | 0,0.8 A | ||
| C. | 9.6×10-5 C,1 A | D. | 1.2×10-4C,0.8 A |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com