
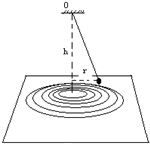
 如图所示,是《用圆锥摆粗略验证向心力的表达式》的实验,用手拨动钢球,使它沿纸上的某个圆周运动,该圆周的半径为r,悬点到圆心的距离为h,用秒表记下钢球从第1次到第n次经过圆上某位置所用的总时间t.
如图所示,是《用圆锥摆粗略验证向心力的表达式》的实验,用手拨动钢球,使它沿纸上的某个圆周运动,该圆周的半径为r,悬点到圆心的距离为h,用秒表记下钢球从第1次到第n次经过圆上某位置所用的总时间t.分析 (1)求得小球转动一周所需时间,根据v=$\frac{2πr}{T}$求得线速度
(2)根据${F}_{向}=\frac{m{v}^{2}}{r}$求得需要的向心力,根据受力分析求得提供的向心力,即可判断
解答 解:(1)小球转动一周所需时间T=$\frac{t}{n-1}$,故线速度v=$\frac{2πr}{T}=\frac{2πr(n-1)}{t}$
(2)作圆周运动所需向心力${F}_{向}=\frac{m{v}^{2}}{r}=\frac{4{π}^{2}mr(n-1)^{2}}{{t}^{2}}$
提供的向心力F=$mg\frac{r}{h}$,故只需验证F向=F,即$\frac{4{π}^{2}(n-1)^{2}}{{t}^{2}}=\frac{g}{h}$,因此小球的质量不需要测量
故答案为:(1)$\frac{2πr(n-1)}{t}$;(2)$\frac{4{π}^{2}(n-1)^{2}}{{t}^{2}}=\frac{g}{h}$,不需要
点评 通过实验数据来粗略验证向心力表示式,培养学生善于分析问题与解决问题的能力,同时运用力的分解寻找向心力的来源


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中物理 来源: 题型:实验题
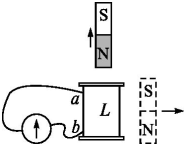 为判断线圈绕向,可将灵敏电流计G与线圈L连接,如图所示,已知线圈由a端开始绕至b端,当电流从电流计G左端流入时,指针向左偏转.
为判断线圈绕向,可将灵敏电流计G与线圈L连接,如图所示,已知线圈由a端开始绕至b端,当电流从电流计G左端流入时,指针向左偏转.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | t=1.5s | B. | v0=10m/s | C. | t=2s | D. | 5$\sqrt{3}$m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,套在条形磁铁外的三个线圈,其面积S1>S2=S3,且“3”线圈在磁铁的正中间.设各线圈中的磁通量依次为φ1、φ2、φ3则它们的大小关系是( )
如图所示,套在条形磁铁外的三个线圈,其面积S1>S2=S3,且“3”线圈在磁铁的正中间.设各线圈中的磁通量依次为φ1、φ2、φ3则它们的大小关系是( )| A. | φ1>φ2>φ3 | B. | φ1<φ2<φ3 | C. | φ1>φ2=φ3 | D. | φ1<φ2=φ3 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{1}{6}$$\sqrt{gR}$ | B. | $\sqrt{gR}$ | C. | $\frac{1}{3}$$\sqrt{gR}$ | D. | $\sqrt{3gR}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
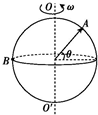
| A. | A、B两点的角速度相等 | B. | A、B两点的线速度相等 | ||
| C. | 若θ=30°,则vA:vB=1:2 | D. | 若θ=30°,则vA:vB=$\sqrt{3}$:2 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,绝缘轨道CDGH位于竖直平面内,圆弧段DG的圆心角为θ=37°,DG与水平段CD、倾斜段GH分别相切于D点和G点,CD段粗糙,DGH段光滑,在H处固定一垂直于轨道的绝缘挡板,整个轨道处于场强为E=1×104N/C、水平向右的匀强电场中.一质量m=4×10-3kg、带电量q=+3×10-6C的小滑块在C处由静止释放,经挡板碰撞后滑回到CD段的中点P处时速度恰好为零.已知CD段长度L=0.8m,圆弧DG的半径r=0.2m;不计滑块与挡板碰撞时的动能损失,滑块可视为质点.求:
如图所示,绝缘轨道CDGH位于竖直平面内,圆弧段DG的圆心角为θ=37°,DG与水平段CD、倾斜段GH分别相切于D点和G点,CD段粗糙,DGH段光滑,在H处固定一垂直于轨道的绝缘挡板,整个轨道处于场强为E=1×104N/C、水平向右的匀强电场中.一质量m=4×10-3kg、带电量q=+3×10-6C的小滑块在C处由静止释放,经挡板碰撞后滑回到CD段的中点P处时速度恰好为零.已知CD段长度L=0.8m,圆弧DG的半径r=0.2m;不计滑块与挡板碰撞时的动能损失,滑块可视为质点.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com