
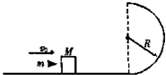
 ��ͼ��ʾ���⻬��Բ�����ֱ���ã��뾶ΪR��һˮƽ�����Բ������У���ˮƽ�⻬�����ͣ��һ������ΪM=0.99kg��ľ�飬һ������Ϊm=0.01kg���ӵ�����v0=400m/s��ˮƽ�ٶ�����ľ���У�Ȼ��һ���˶��������ߵ�ˮƽ�׳���gȡ10m/s2������
��ͼ��ʾ���⻬��Բ�����ֱ���ã��뾶ΪR��һˮƽ�����Բ������У���ˮƽ�⻬�����ͣ��һ������ΪM=0.99kg��ľ�飬һ������Ϊm=0.01kg���ӵ�����v0=400m/s��ˮƽ�ٶ�����ľ���У�Ȼ��һ���˶��������ߵ�ˮƽ�׳���gȡ10m/s2���������� ��1���ӵ�����ľ��Ĺ����У��ӵ���ľ����ɵ�ϵͳ�����غ㣬���ݶ����غ㶨������ӵ�����ľ�����ٶȣ�
��2�����������غ�����ӵ�����ľ�������ϵͳ���������ܣ�
��3�����ݻ�е���غ㶨���������Բ�����ߵ���ٶȣ���ϸ߶����ƽ���˶���ʱ�䣬�Ӷ��ó�ˮƽ����ı���ʽ��ͨ�����κ�����ֵ�ķ������ˮƽ�������ʱR�Ĵ�С��
��� �⣺��1�����ӵ���ľ��Ӧ�ö����غ㶨�ɣ��涨�ӵ��ķ���Ϊ�������ݶ����غ㶨���У�mv0=��m+M��v1
�������ݽ��v1=4m/s
��2���ӵ���ľ�����õĹ����У����������ܵ���ϵͳ���ܵļ��������У�$Q=\frac{1}{2}m{v_0}^2-\frac{1}{2}��m+m��{v_1}^2$
�������ݽ��Q=792J
ȡˮƽ��Ϊ�������棬��ľ�鵽��ߵ�ʱ���ٶ�Ϊv2����$\frac{1}{2}��m+M��{v_1}^2=\frac{1}{2}��m+M��v_2^2+��m+M��g•2R$
����${v_2}=\sqrt{16-40R}$
���˶��ķֽ�֪��$2R=\frac{1}{2}g{t^2}$
S=v2t
���$S=4��\sqrt{\frac{{-10{R^2}+4R}}{10}}$
��R=0.2mʱˮƽ����������ֵSmax=0.8m��
�𣺣�1���ӵ�����ľ�����ٶ�Ϊ4m/s��
��2���ӵ�����ľ�������ϵͳ����������Ϊ792J
��3����Բ����뾶RΪ0.2mʱ��ƽ��ˮƽ���������������0.8m��
���� ���⿼���˶����غ㶨�ɡ������غ㶨�ɺͻ�е���غ㶨�ɵ��ۺ����ã��ۺ��Խ�ǿ����ѧ��������Ҫ��ϸߣ����ڵ����ʣ�����ѧ֪ʶ��ϵ�ȽϽ��ܣ����ǿ�ⷽ���ѵ����


 ������ҵ��ͬ����ϰ��ϵ�д�
������ҵ��ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
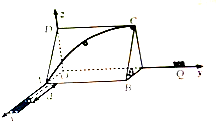 ��ͼ��һ�����α���ABCD�ı߳�ΪR�������Ϲ̶�һ���������εı߳�Ϊ�뾶���ķ�֮һ�⻬Բ�������忿����ˮƽ����н�Ϊ�ȵ�ǽ���ϣ�������άֱ������ϵ��ozΪ��ֱ�ᣬxOyΪˮƽ���森���ڵ����ϵĵ���ǹǹ����AB�ߵľ���Ϊd������ǹ���䴦��С����ˮƽ�������˶�һ�ξ���d��A����ʼ����Բ���ڲ���ϱ��壬����Բ������ߵ�Cˮƽ�ɳ������ڷ�����y��ij����СͰQ�ڣ���֪С�������ͱ����Ķ�Ħ��������Ϊ�̣�����С���ڹս�A���Ļ�е����ʧ����
��ͼ��һ�����α���ABCD�ı߳�ΪR�������Ϲ̶�һ���������εı߳�Ϊ�뾶���ķ�֮һ�⻬Բ�������忿����ˮƽ����н�Ϊ�ȵ�ǽ���ϣ�������άֱ������ϵ��ozΪ��ֱ�ᣬxOyΪˮƽ���森���ڵ����ϵĵ���ǹǹ����AB�ߵľ���Ϊd������ǹ���䴦��С����ˮƽ�������˶�һ�ξ���d��A����ʼ����Բ���ڲ���ϱ��壬����Բ������ߵ�Cˮƽ�ɳ������ڷ�����y��ij����СͰQ�ڣ���֪С�������ͱ����Ķ�Ħ��������Ϊ�̣�����С���ڹս�A���Ļ�е����ʧ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ���������巨��֤��е���غ㶨�ɵ�ʵ�飮
���������巨��֤��е���غ㶨�ɵ�ʵ�飮�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ���պϵ��߿���������Ժ��Բ��ƣ�������ͼʾλ������������ǿ�ų�������һ����0.3sʱ���������������Ĺ�ΪW1��ͨ�����߽���ĵ����Ϊq1���ڶ�����0.9sʱ�����������������Ĺ�ΪW2��ͨ�����߽���ĵ����Ϊq2��������
��ͼ��ʾ���պϵ��߿���������Ժ��Բ��ƣ�������ͼʾλ������������ǿ�ų�������һ����0.3sʱ���������������Ĺ�ΪW1��ͨ�����߽���ĵ����Ϊq1���ڶ�����0.9sʱ�����������������Ĺ�ΪW2��ͨ�����߽���ĵ����Ϊq2��������| A�� | W1��W2��q1��q2 | B�� | W1��W2��q1=q2 | C�� | W1��W2��q1=q2 | D�� | W1��W2��q1��q2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��

| A�� | ��t1ʱ�̣������Ȧ�еĴų������ | |
| B�� | ��t1��t2�������������ϵĴ���������ϼ��� | |
| C�� | ��t2��t3�������Ȧ�еĴų��ܲ������� | |
| D�� | ��t4ʱ�̣��������еĵ糡ǿ��Ϊ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �Ȼ��У�ȼ�����ܲ�����ȫ��ת��Ϊ��е�� | |
| B�� | һ������Ļ�е�ܲ�����ȫ��ת��Ϊ���� | |
| C�� | �ڻ���������У�ȼ�������ܲ�����ȫ��ת��Ϊ���� | |
| D�� | ���ȴ����У������������Է��شӵ������崫�ݸ��������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
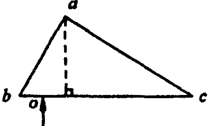 ��ͼΪһֱ���⾵�ĺ���棬��bac=90�㣬��abc=60�㣮һƽ��ϸ������O���ش�ֱ��bc��ķ��������⾵����֪�⾵���ϵ�������n=$\sqrt{2}$����������ԭ�������bc���ϵķ���⣬���й��ߣ�������
��ͼΪһֱ���⾵�ĺ���棬��bac=90�㣬��abc=60�㣮һƽ��ϸ������O���ش�ֱ��bc��ķ��������⾵����֪�⾵���ϵ�������n=$\sqrt{2}$����������ԭ�������bc���ϵķ���⣬���й��ߣ�������| A�� | ��ab����� | B�� | ���ܴ�ac����� | ||
| C�� | ��bc�����������bc��б�� | D�� | ��bc�����������bc�洹ֱ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | $\frac{x_1}{x_2}=\frac{t_1}{t_2}$ | B�� | $\frac{x_1}{t_1}=\frac{x_2}{t_2}=\frac{{{x_1}+{x_2}}}{{{t_1}+{t_2}}}$ | ||
| C�� | $\frac{a_1}{a_2}=\frac{t_1}{t_2}$ | D�� | $v=\frac{{2��{x_1}+{x_2}��}}{{{t_1}+{t_2}}}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com