
 ��ͼ��ʾ���⻬��Ե�İ�Բ�����ֱ���ã�ֱ��ADˮƽ��B��C�����ȷֵ㣬��A��D����̶��е����ΪQ1��Q2�������ɣ����������ϵ��Q1=3$\sqrt{3}$Q2���ҹ涨����Զ������Ϊ0������������Q��Χ�ռ����ĵ���Ϊ��=k$\frac{Q}{r}$��Q��ʾ������k��ʾ������������r��ʾij�㵽���ɵľ��룮������˵����ȷ���ǣ�������
��ͼ��ʾ���⻬��Ե�İ�Բ�����ֱ���ã�ֱ��ADˮƽ��B��C�����ȷֵ㣬��A��D����̶��е����ΪQ1��Q2�������ɣ����������ϵ��Q1=3$\sqrt{3}$Q2���ҹ涨����Զ������Ϊ0������������Q��Χ�ռ����ĵ���Ϊ��=k$\frac{Q}{r}$��Q��ʾ������k��ʾ������������r��ʾij�㵽���ɵľ��룮������˵����ȷ���ǣ�������| A�� | B����C��ij�ǿ��С֮��ΪEB��EC=$\sqrt{61}$��6 | |
| B�� | B����C��ij�ǿ��С֮��ΪEB��EC=2$\sqrt{61}$��3 | |
| C�� | B����C��ĵ��ƴ�С֮��Ϊ��B����C=5$\sqrt{3}$��6 | |
| D�� | B����C��ĵ��ƴ�С֮��Ϊ��B����C=5$\sqrt{3}$��3 |
���� ���ݿ��ض��ɷֱ�д������������B����C��ĵ糡ǿ�ȵı���ʽ����������ĵ糡ǿ�ȵķ�����ʸ���ϳɵķ�����������糡ǿ�ȣ�������Ŀ�ṩ�ĵ����ܵı���ʽ���ֱ������Ȼ����ͼ��ɣ�
��� �⣺A�����Բ�İ뾶ΪR�����ɼ��ι�ϵ��֪��AB֮��ľ���ΪR��CD֮��ľ���ΪR��AC��BD֮��ľ��붼�ǣ�$\frac{R}{sin30��}•sin120��=\sqrt{3}R$
A��D�ֱ���B������ĵ糡ǿ�ȣ�${E}_{BA}=\frac{k{Q}_{1}}{{R}^{2}}$=$3\sqrt{3}\frac{k{Q}_{2}}{{R}^{2}}$��${E}_{BD}=\frac{k•{Q}_{2}}{{��\sqrt{3}R��}^{2}}=\frac{k{Q}_{2}}{3{R}^{2}}$������ͼ����֪�����ֳ�ǿ�ķ��������ֱ�ģ�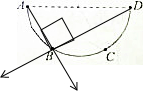
���ݼ��ι�ϵ��֪��������ʸ���ķ������ֱ��������ϳ�ǿΪ��${E}_{B}=\sqrt{{E}_{BA}^{2}+{E}_{BD}^{2}}$=$\frac{2}{3}\sqrt{61}•\frac{k{Q}_{2}}{{R}^{2}}$
A��D�ֱ���c������ĵ糡ǿ�ȣ�${E}_{CA}=\frac{k{Q}_{1}}{{��\sqrt{3}R��}^{2}}=\frac{1}{3}•\frac{3\sqrt{3}k{Q}_{2}}{{R}^{2}}=\sqrt{3}\frac{k{Q}_{2}}{{R}^{2}}$��${E}_{CD}=\frac{k•{Q}_{2}}{{R}^{2}}$
���ݼ��ι�ϵ����ϳ�ǿΪ��${E}_{C}=\sqrt{{E}_{CA}^{2}+{E}_{CD}^{2}}$=$\frac{2k•{Q}_{2}}{{R}^{2}}$
���ԣ�$\frac{{E}_{B}}{{E}_{C}}=\frac{\frac{2}{3}\sqrt{61}}{2}=\frac{\sqrt{61}}{3}$����AB����
C������A��B������ĵ��ƣ�${��}_{AB}=\frac{k{Q}_{1}}{R}=\frac{3\sqrt{3}k{Q}_{2}}{R}$��
��C������ĵ��ƣ�${��}_{AC}=\frac{k{Q}_{1}}{\sqrt{3}R}=\frac{3k{Q}_{2}}{R}$
����D��B�������ĵ��ƣ�${��}_{DB}=\frac{k{Q}_{2}}{\sqrt{3}R}$��
��C������ĵ��ƣ�${��}_{DC}=\frac{k{Q}_{2}}{R}$
����B����ܵ��ƣ�${��}_{B}={��}_{AB}+{��}_{DB}=��\frac{\sqrt{3}}{3}+3\sqrt{3}��\frac{k{Q}_{2}}{R}$
D����ܵ��ƣ���C=��DC+��AC=$\frac{4k{Q}_{2}}{R}$
���ԣ���B����C=$\frac{3\sqrt{3}+\frac{\sqrt{3}}{3}}{4}=\frac{5\sqrt{3}}{6}$����C��ȷ��D����
��ѡ��C
���� ���⿼����ض��ɺ�ʸ���ĺϳɣ�����Ĺؼ�����ȷ�жϳ�������������B��C���ĵ糡ǿ�ȵĴ�С������Ҫע��ʹ��ʸ���ϳɵķ�����ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��������ͬ��A��B��������ھ�ֹ״̬������С��������Խ���Ƭ��ʹA����ˮƽ�����׳���B��ͬʱ���ɿ����������䣮������˵������ȷ���� ��������
��ͼ��ʾ��������ͬ��A��B��������ھ�ֹ״̬������С��������Խ���Ƭ��ʹA����ˮƽ�����׳���B��ͬʱ���ɿ����������䣮������˵������ȷ���� ��������| A�� | B������� | |
| B�� | ����ͬʱ��� | |
| C�� | ������ͬʱ��أ�Ҳ����֤��A������ֱ������˶������������˶� | |
| D�� | �������ʱ�ٶȴ�С��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ����ֱ��������M0NΪ�߽���н���ǿ�ų����Ÿ�Ӧǿ��ΪB������ֱֽ�����⣬��M=60�㣬P��ΪMN���е㣮��O�����һ������Դ��������ON�����䲻ͬ���ʵ�ij�ִ��������ӣ������������ܵ��������������ӽ���ų�����˶������������
��ͼ��ʾ����ֱ��������M0NΪ�߽���н���ǿ�ų����Ÿ�Ӧǿ��ΪB������ֱֽ�����⣬��M=60�㣬P��ΪMN���е㣮��O�����һ������Դ��������ON�����䲻ͬ���ʵ�ij�ִ��������ӣ������������ܵ��������������ӽ���ų�����˶������������| A�� | �����п��ܴ�M�� | |
| B�� | ��ֱMN�����������ֻ��ͨ��P�� | |
| C�� | �����ٶ�Խ���ڴų����˶���ʱ��Խ�� | |
| D�� | ���ܴ�ֱ��OM������������ڴų����˶���ʱ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 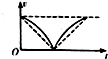 | B�� | 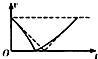 | C�� | 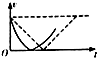 | D�� | 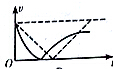 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
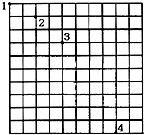 ij������ȤС��Ϊ��̽��ƽ���˶��Ĺ��ɣ���С��ˮƽ�׳�����Ƶ����������������࣬�õ�����ͼ��ʾ����Ƭ������3��4��λ��֮����û�����㵽���֣���֪ÿ��С����߳�19.6cm�����ص��������ٶ�Ϊg=9.8m/s2��������ø�ʽ��ʾ��
ij������ȤС��Ϊ��̽��ƽ���˶��Ĺ��ɣ���С��ˮƽ�׳�����Ƶ����������������࣬�õ�����ͼ��ʾ����Ƭ������3��4��λ��֮����û�����㵽���֣���֪ÿ��С����߳�19.6cm�����ص��������ٶ�Ϊg=9.8m/s2��������ø�ʽ��ʾ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
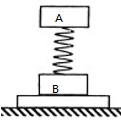 ��ͼ���ᵯ�ɵľ���ϵ��Ϊk���϶���һ����Ϊm��ľ��A�������¶�����һ����Ϊm��ľ��B����������ϵͳ����ˮƽ���ϲ����ھ�ֹ״̬��������ֱ���ϵĺ���F��ľ��Aʹ֮�����˶�����B��Ҫ�뿪����ʱ��A���ٶ�Ϊv0������
��ͼ���ᵯ�ɵľ���ϵ��Ϊk���϶���һ����Ϊm��ľ��A�������¶�����һ����Ϊm��ľ��B����������ϵͳ����ˮƽ���ϲ����ھ�ֹ״̬��������ֱ���ϵĺ���F��ľ��Aʹ֮�����˶�����B��Ҫ�뿪����ʱ��A���ٶ�Ϊv0������| A�� | F��������Aʱ��A�ļ��ٶ�ֵΪ$\frac{F}{2m}$ | |
| B�� | ��F������A��B���뿪����Ĺ����У�A�����ĸ߶�Ϊ$\frac{2mg}{k}$ | |
| C�� | ��B���뿪����ʱ��A�ļ��ٶ�ֵΪ$\frac{F}{m}$ | |
| D�� | ��B���뿪����ʱ�����ɶ�B������˲ʱ����ΪFv |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
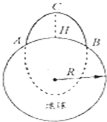 ������һ41���ʵ�����������Ŀǰ�ҹ�����������Ƚ���ս�Ժ˵���֮һ���ʵ���������Ҫ�ڴ�������������Բ�������������У�����뾶����ij���ԼΪ0.5����1������뾶���ǹ����������ϰ�е�������������ǹ�����ܻ��Ƶ���һ�ܣ���ͼΪ������-41�����乥��ʾ��ͼ�������ӵ�����A�����ٶ�v0���䣬�ڵ������������£�����Բ������У����е����ϵ�Ŀ��B��CΪ��Բ��Զ�ص㣬�����߶�ΪH����֪����뾶ΪR�����������������ٶ�Ϊg�������ǿ�������������������
������һ41���ʵ�����������Ŀǰ�ҹ�����������Ƚ���ս�Ժ˵���֮һ���ʵ���������Ҫ�ڴ�������������Բ�������������У�����뾶����ij���ԼΪ0.5����1������뾶���ǹ����������ϰ�е�������������ǹ�����ܻ��Ƶ���һ�ܣ���ͼΪ������-41�����乥��ʾ��ͼ�������ӵ�����A�����ٶ�v0���䣬�ڵ������������£�����Բ������У����е����ϵ�Ŀ��B��CΪ��Բ��Զ�ص㣬�����߶�ΪH����֪����뾶ΪR�����������������ٶ�Ϊg�������ǿ�������������������| A�� | ��C��ʱ�ļ��ٶ�ֵΪ$\frac{g{R}^{2}}{��R+H��^{2}}$ | |
| B�� | ��C��ʱ������ΪR$\sqrt{\frac{g}{R+H}}$ | |
| C�� | ����B��ʱ������Ϊv0 | |
| D�� | ��C��B�Ĺ����������Ĺ����ȼ�С������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ͬ�����Ǻ�������ǵ����ٶ�֮��Ϊ2��1 | |
| B�� | ͬ�����ǵĺ�������ǵĽ��ٶ�֮��Ϊ8��1 | |
| C�� | �پ���$\frac{12}{7}$h�������Ǿ�����Զ | |
| D�� | �پ���$\frac{6}{7}$h�������Ǿ�����Զ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
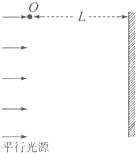 ijһ������ȤС�飬���������һ�о�ƽ���˶����ɵ�ʵ�飬��ͼ��ʾ��O����С��ƽ���˶��ij�ʼλ�ã���O�������һ��Ƶ��ˮƽƽ�й�Դ������Ƶ��Ϊf�����׳������ǰ������ֱ����һ��ë��������С���׳�ʱƽ�й�Դ��ʼ���⣮��ƽ�й�Դ����ʱ����ë��������С���һ��ͶӰ�㣮��֪ͼ��O����ë����ˮƽ����L����õ�һ������ͶӰ��֮��ľ���Ϊy��ȡ�������ٶ�g����С��ڶ�������ͶӰ��֮��ľ���Ϊ3y�����С����v0�׳�ʱ��ǡ��������ë�����ĵˣ��ܹ۲쵽$\frac{Lf}{{v}_{0}}+1$��ͶӰ��
ijһ������ȤС�飬���������һ�о�ƽ���˶����ɵ�ʵ�飬��ͼ��ʾ��O����С��ƽ���˶��ij�ʼλ�ã���O�������һ��Ƶ��ˮƽƽ�й�Դ������Ƶ��Ϊf�����׳������ǰ������ֱ����һ��ë��������С���׳�ʱƽ�й�Դ��ʼ���⣮��ƽ�й�Դ����ʱ����ë��������С���һ��ͶӰ�㣮��֪ͼ��O����ë����ˮƽ����L����õ�һ������ͶӰ��֮��ľ���Ϊy��ȡ�������ٶ�g����С��ڶ�������ͶӰ��֮��ľ���Ϊ3y�����С����v0�׳�ʱ��ǡ��������ë�����ĵˣ��ܹ۲쵽$\frac{Lf}{{v}_{0}}+1$��ͶӰ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com