
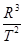 =k,k与中心体有关.
=k,k与中心体有关.

 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
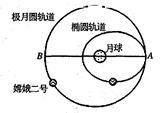
 2010年10月1日,“嫦娥二号”卫星在西昌卫星发射中心成功发射.如图所示为嫦娥一号、二号卫星先后绕月做匀速圆周运动的示意图,“嫦娥一号”在轨道I上运行,距月球表面高度为200km;“嫦娥二号”在轨道II上运行,距月球表面高度为100km.根据以上信息可知( )
2010年10月1日,“嫦娥二号”卫星在西昌卫星发射中心成功发射.如图所示为嫦娥一号、二号卫星先后绕月做匀速圆周运动的示意图,“嫦娥一号”在轨道I上运行,距月球表面高度为200km;“嫦娥二号”在轨道II上运行,距月球表面高度为100km.根据以上信息可知( )查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
 (2011?昌平区二模)2010年10月1日我国成功利用长征三号甲运载火箭将探月卫星“嫦娥二号”发射成功.经过两次太空“刹车”,“嫦娥二号”卫星在距月球表面100公里的极月圆轨道上绕月飞行.相比2007年10月24日发射的“嫦娥一号”(绕月运行高度为200公里,运行周期127分钟),更接近月球表面,成像更清晰.根据以上信息,下列判断正确的是( )
(2011?昌平区二模)2010年10月1日我国成功利用长征三号甲运载火箭将探月卫星“嫦娥二号”发射成功.经过两次太空“刹车”,“嫦娥二号”卫星在距月球表面100公里的极月圆轨道上绕月飞行.相比2007年10月24日发射的“嫦娥一号”(绕月运行高度为200公里,运行周期127分钟),更接近月球表面,成像更清晰.根据以上信息,下列判断正确的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com