
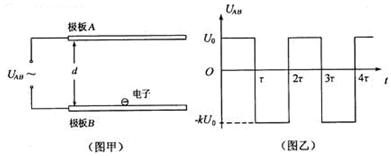
分析 (1)电子在0~τ时间内做匀加速运动,在τ~2τ时间内先做匀减速运动,后反向做初速度为零的匀加速运动,电子不能到达极板A的条件为电子运动位移之和小于板间距离
(2)电子2n~(2n+1)τ时间内向下匀加速直线运动,在(2n+1)~2(n+1)τ时间内做向下做匀减速直线运动,求出一个电压变化周期内电子速度的增量,在求任意时间电子的速度随时间的变化规律
(3)电子在第N个周期内的位移是在2(N-1)τ~(2N-1)τ时间内的位移与电子在(2N-1)τ~2Nτ时间内的位移的矢量和,求出表达式,利用位移为零得到k的表达式
解答 解:(1)电子在0~T时间内做匀加速运动
加速度的大小a1=$\frac{{e{U_0}}}{md}$ ①
位移x1=$\frac{1}{2}$a1T2 ②
在T-2T时间内先做匀减速运动,后反向做匀加速运动
加速度的大小a2=$\frac{{5e{U_0}}}{4md}$ ③
初速度的大小v1=a1T ④
匀减速运动阶段的位移x2=$\frac{{{v_1}^2}}{{2{a_2}}}$⑤
依据题意d>x1+x2解得d>$\sqrt{\frac{{9e{U_0}{T^2}}}{10m}}$⑥
(2)在2nT~(2n+1)T,(n=0,1,2,…,99)时间内
加速度的大小a′2=$\frac{ek{U}_{0}}{md}$⑦
速度增量△v2=-a′2T⑧
(a)当0≤t-2nt<T时
电子的运动速度v=n△v1+n△v2+a1(t-2nT)⑨
解得v=[t-(k+1)nT]$\frac{{ek{U_0}}}{md}$,(n=0,1,2,…,99)(10)
(b)当0≤t-(2n+1)T<T时,电子的运动速度v=(n+1)△v1+n△v2-a′2[t-(2n+1)T](11)
解得v=[(n+1)(k+1)T-kt]$\frac{{e{U_0}}}{dm}$,(n=0,1,2,…,99)(12)
(3)电子在2(N-1)T~(2N-1)T时间内的位移x2N-1=v2N-2T+$\frac{1}{2}$a1T2
电子在(2N-1)T~2NT时间内的位移x2N=v2N-1T-$\frac{1}{2}$a′2T2
由(10)式可知v2N-2=(N-1)(1-k)T$\frac{{e{U_0}}}{dm}$
由(12)式可知v2N-1=(N-Nk+k)T$\frac{{e{U_0}}}{dm}$
依据题意x2N-1+x2N=0
解得k=$\frac{4N-1}{4N-3}$;
答:(1)d应满足的条件为d>$\sqrt{\frac{{9e{U_0}{T^2}}}{10m}}$;
(2)(a)当0≤t-2nτ<τ时,v=[t-(k+1)nτ]$\frac{{e{U_0}}}{dm}$,(n=0,1,2,3…99);
(b)当0≤t-(2n+1)τ<τ时,v=[(n+1)(k+1)T-kt]$\frac{{e{U_0}}}{dm}$,(n=0,1,2,…,99);
(3)k的值为$\frac{4N-1}{4N-3}$.
点评 电子在交变电场中的变加速运动问题是考察的热点,重要的是分析清楚电子的运动情景,同时这种问题运算量较大,过程较为复杂,给学生造成较大的难度.


科目:高中物理 来源: 题型:计算题
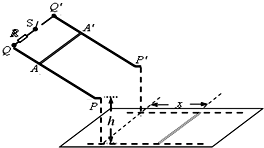 如图所示,宽度为L的粗糙平行金属导轨PQ和P′Q′倾斜放置,顶端QQ′之间连接一个阻值为R的电阻和开关S,底端PP′处与一小段水平轨道用光滑圆弧相连.已知底端PP′离地面的高度为h,倾斜导轨处于垂直于导轨平面向上的匀强磁场(图中未画出)中.若断开开关S,一根质量为m、电阻为r、长也为L的金属棒从AA′处由静止开始滑下,金属棒落地点离PP′的水平距离为x1;若闭合开关S,该金属棒仍从AA′处由静止开始滑下,则金属棒落地点离PP′的水平距离为x2.不计导轨电阻,忽略金属棒经过PP′处的机械能损失,已知重力加速度为g,求:
如图所示,宽度为L的粗糙平行金属导轨PQ和P′Q′倾斜放置,顶端QQ′之间连接一个阻值为R的电阻和开关S,底端PP′处与一小段水平轨道用光滑圆弧相连.已知底端PP′离地面的高度为h,倾斜导轨处于垂直于导轨平面向上的匀强磁场(图中未画出)中.若断开开关S,一根质量为m、电阻为r、长也为L的金属棒从AA′处由静止开始滑下,金属棒落地点离PP′的水平距离为x1;若闭合开关S,该金属棒仍从AA′处由静止开始滑下,则金属棒落地点离PP′的水平距离为x2.不计导轨电阻,忽略金属棒经过PP′处的机械能损失,已知重力加速度为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,一价氢离子${\;}_{1}^{1}$H和二价氦离子${\;}_{2}^{4}$He(重力不计),分别先后经过同一加速电场加速后,垂直射入同一偏转电场中,偏转后,打在同一荧屏上,则它们( )
如图所示,一价氢离子${\;}_{1}^{1}$H和二价氦离子${\;}_{2}^{4}$He(重力不计),分别先后经过同一加速电场加速后,垂直射入同一偏转电场中,偏转后,打在同一荧屏上,则它们( )| A. | 在两个电场中运动的总时间相同 | |
| B. | 打在荧光屏上的同一点 | |
| C. | 到达屏上的动能相同 | |
| D. | 氦离子到达屏上时的动能是氢离子的两倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
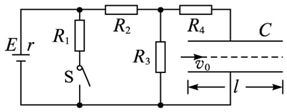
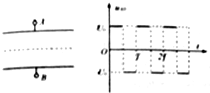 一对平行金属板长为L,两板间距为d,质量为m,电荷量为e的电子从平行板左侧以速度υ0沿两板的中线不断进入平行板之间,两板间所加交变电压UAB,如图所示,交变电压的周期,已知所有电子都能穿过平行板,且最大偏距的粒子刚好从极板的边缘飞出,不计重力作用,则( )
一对平行金属板长为L,两板间距为d,质量为m,电荷量为e的电子从平行板左侧以速度υ0沿两板的中线不断进入平行板之间,两板间所加交变电压UAB,如图所示,交变电压的周期,已知所有电子都能穿过平行板,且最大偏距的粒子刚好从极板的边缘飞出,不计重力作用,则( )| A. | 所有电子都从右侧的同一点离开电场 | |
| B. | 所有电子离开电场时速度都是υ0 | |
| C. | t=0时刻进入电场的电子,离开电场时动能最大 | |
| D. | t=$\frac{T}{4}$时刻进入电场的电子,在两板间运动时最大侧位移为$\frac{d}{16}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
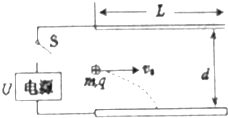 如图所示,水平放置的平行板电容器,与某一电源相连,它的极板长L=0.4m,两板间距离d=4×10-3m,有一束由相同带电微粒组成的粒子流,以相同的速度v0从两板中央平行极板射入,开关S闭合前,两板不带电,由于重力作用微粒能落到下板的正中央,已知微粒质量为m=4×10-5kg,电荷量q=1×10-8C,(g取10m/s2)求:
如图所示,水平放置的平行板电容器,与某一电源相连,它的极板长L=0.4m,两板间距离d=4×10-3m,有一束由相同带电微粒组成的粒子流,以相同的速度v0从两板中央平行极板射入,开关S闭合前,两板不带电,由于重力作用微粒能落到下板的正中央,已知微粒质量为m=4×10-5kg,电荷量q=1×10-8C,(g取10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
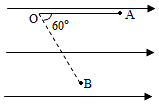 长为L细线,上端固定,下端栓一质量为m、带电量为q的球,处于如图所示的水平向右的匀强电场中,开始时,将细线与小球拉成水平,然后释放,小球由静止开始向下摆动,当细杆转动60°角时,小球到达B点,且速度恰好为零,求:
长为L细线,上端固定,下端栓一质量为m、带电量为q的球,处于如图所示的水平向右的匀强电场中,开始时,将细线与小球拉成水平,然后释放,小球由静止开始向下摆动,当细杆转动60°角时,小球到达B点,且速度恰好为零,求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,有一束电子流在经电压U=5000V的加速电压加速后,在距两极板等距处垂直进入平行板间的匀强电场,若两板间距为d=1.0cm,板长 L=5.0cm,要使电子能从两板间飞出,两个极板上最多能加多大电压?
如图所示,有一束电子流在经电压U=5000V的加速电压加速后,在距两极板等距处垂直进入平行板间的匀强电场,若两板间距为d=1.0cm,板长 L=5.0cm,要使电子能从两板间飞出,两个极板上最多能加多大电压?查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com