
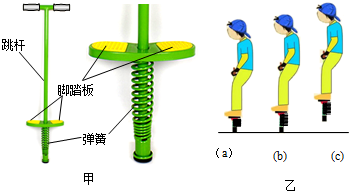
分析 (1)画出小孩从A到B再到C的过程中弹簧弹力与弹簧压缩量x对应的图象,根据F-x图的面积代表F所做的功的大小,求得弹力做的功W,列式分析.
(2)在整个预备动作阶段,小孩做的功等于其机械能的变化量与弹簧弹性势能变化量之和.
(3)正式运动阶段,当弹跳杆触地前瞬间,弹簧处于原长状态,由机械能守恒定律可知,小孩和弹跳杆的速度均为v1.弹跳杆触地瞬间,杆的速度减为0,小孩保持v1的速度.此后小孩以v1的初速度向下压缩弹簧,由能量守恒可知,为使每个周期内弹簧的最大压缩量为3x0,根据功能关系求解.
解答 解:(1)画出弹簧弹力F的大小与弹簧压缩量x关系图如图,F-x图的面积代表F所做的功的大小.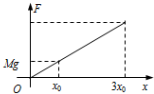
下降阶段,弹簧压缩量从x0到xm的过程,弹簧弹力做负功,为
W1=-$\frac{1}{2}$(kx0+kxm)(xm-x0)=$\frac{1}{2}$kx02-$\frac{1}{2}$kxm2.
上升阶段,弹簧压缩量从xm到2x0的过程,弹簧弹力做正功,为
W2=+$\frac{1}{2}$[kxm+k(2x0)](xm-2x0)=$\frac{1}{2}$kxm2-$\frac{1}{2}$k(2x0)2
则弹簧弹力做的功 W=W1+W2=$\frac{1}{2}$kx02-$\frac{1}{2}$kxm2+$\frac{1}{2}$kxm2-$\frac{1}{2}$k(2x0)2=-$\frac{3}{2}$kx02,与xm无关.
(2)由功能关系可知,在预备阶段,小孩至少需做的功W′应满足
W′=△Ek+△EpG+△Ep弹=0+[-Mg(3x0-x0)]+[$\frac{1}{2}$k(3x0)2-$\frac{1}{2}$kx02]=2Mgx0
(3)正式运动阶段,当弹跳杆触地前瞬间,弹簧处于原长状态,由机械能守恒定律可知,小孩和弹跳杆的速度均为v1.弹跳杆触地瞬间,杆的速度减为0,小孩保持v1的速度.此后小孩以v1的初速度向下压缩弹簧,由能量守恒可知,为使每个周期内弹簧的最大压缩量为3x0,至少需要给(小孩和弹跳杆)系统补充的能量E满足
E=△Ek+△EpG+△Ep弹=[0-$\frac{1}{2}$Mv12]+[-Mg(3x0)]+[$\frac{1}{2}$k(3x0)2-0]=$\frac{3}{2}$[1-$\frac{{M}^{2}}{(M+m)^{2}}$]Mgx0=$\frac{3(2M+m)Mmg{x}_{0}}{2(M+m)^{2}}$
答:(1)小孩从A到B再到C的过程中弹簧弹力做的功W为-$\frac{3}{2}$kx02,与xm无关.
(2)小孩至少需做的功W′为2Mgx0.
(3)正式运动阶段每个周期内,小孩至少需要给系统(小孩和弹跳杆)补充的能量E为$\frac{3(2M+m)Mmg{x}_{0}}{2(M+m)^{2}}$.
点评 本题考查机械能守恒定律的应用,要注意正确分析全过程,明确弹簧的弹性势能与重力势能之间的转化及守恒规律的应用,即注意能量转化的方向问题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中物理 来源: 题型:解答题
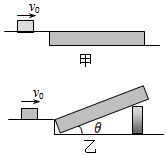 如图甲所示,光滑平台右侧与一长为L=2.5m的水平木板相接,木板固定在地面上,现有一小滑块以初速度v0=5m/s滑上木板,恰好滑到木板右端停止.现让木板右端抬高,如图乙所示,使木板与水平地面的夹角θ=37°,让滑块以相同的初速度滑上木板,不计滑块滑上木板时的能量损失,g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图甲所示,光滑平台右侧与一长为L=2.5m的水平木板相接,木板固定在地面上,现有一小滑块以初速度v0=5m/s滑上木板,恰好滑到木板右端停止.现让木板右端抬高,如图乙所示,使木板与水平地面的夹角θ=37°,让滑块以相同的初速度滑上木板,不计滑块滑上木板时的能量损失,g=10m/s2,sin37°=0.6,cos37°=0.8.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
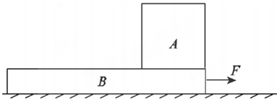 如图所示,A、B两物块的质量分别为2m和m,静止叠放在水平地面上,A、B间的动摩擦因数为μ,B与地面间的动摩擦因数为$\frac{μ}{2}$,最大静摩擦力等于滑动摩擦力,重力加速度为g,现对B施加一水平拉力F,则( )
如图所示,A、B两物块的质量分别为2m和m,静止叠放在水平地面上,A、B间的动摩擦因数为μ,B与地面间的动摩擦因数为$\frac{μ}{2}$,最大静摩擦力等于滑动摩擦力,重力加速度为g,现对B施加一水平拉力F,则( )| A. | 当F<3μmg时,A、B都相对地面静止 | |
| B. | 当F=$\frac{5}{2}$μmg时,A的加速度为$\frac{μg}{3}$ | |
| C. | 当F>6μmg时,A相对B滑动 | |
| D. | 无论F为何值,A的加速度不会超过μg |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
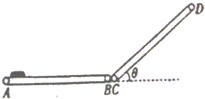 如图是课外活动小组为某仓库设计的一个皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B两端相距3m,另一台倾斜,传送带与地面的倾角θ=37°,C、D两端相距4.45m,B、C相距很近,水平部分AB以5m/s的速率顺时针转动,将一工件轻放在A端,到达B端后,速度大小不变地传到倾斜的CD部分,工件与传送带间的动摩擦因数均为0.5,其最大静摩擦力认为等于滑动摩擦力(sin37°=0.6,cos37°=0.8,g取10m/s2).
如图是课外活动小组为某仓库设计的一个皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B两端相距3m,另一台倾斜,传送带与地面的倾角θ=37°,C、D两端相距4.45m,B、C相距很近,水平部分AB以5m/s的速率顺时针转动,将一工件轻放在A端,到达B端后,速度大小不变地传到倾斜的CD部分,工件与传送带间的动摩擦因数均为0.5,其最大静摩擦力认为等于滑动摩擦力(sin37°=0.6,cos37°=0.8,g取10m/s2).查看答案和解析>>
科目:高中物理 来源: 题型:多选题
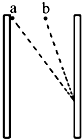 如图所示,竖直放置的两平行金属板间有匀强电场,在两极板间同一等高线上有两质量相等的带电小球a、b(可以看作质点).将小球a、b分别从紧靠左极板和两极板正中央的位置由静止释放,它们沿图中虚线运动,都能打在右极板上的同一点.则从释放小球到刚要打到右极板的运动中,下列说法正确的是( )
如图所示,竖直放置的两平行金属板间有匀强电场,在两极板间同一等高线上有两质量相等的带电小球a、b(可以看作质点).将小球a、b分别从紧靠左极板和两极板正中央的位置由静止释放,它们沿图中虚线运动,都能打在右极板上的同一点.则从释放小球到刚要打到右极板的运动中,下列说法正确的是( )| A. | 它们的运动时间ta>tb | |
| B. | 它们的电荷量之比qa:qb=2:1 | |
| C. | 它们的电势能减少量之比△Epa:△Epb=4:1 | |
| D. | 它们的动能增加量之比△Eka:△Ekb=4:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 第二过程拉力做的功是第一过程拉力做功的3倍 | |
| B. | 第二过程拉力做的功是第一过程拉力做功的8倍 | |
| C. | 第二过程动能增量是第一过程动能增量的3倍 | |
| D. | 第二过程拉力做功的平均功率是第一过程拉力做功的平均功率的4倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 功是能量转化的量度 | |
| B. | 若某一个力对物体不做功,说明该物体一定没有位移 | |
| C. | 因为功有正负,所以其加减适用于平行四边形定则或三角形法则 | |
| D. | 一个恒力对物体做的功等于这个力的大小、物体位移的大小及力和位移夹角的余弦三者的乘积 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
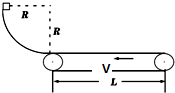 如图所示,一个可视为质点的物块,质量为m=2kg,从光滑四分之一圆弧轨道顶端由静止滑下,到达底端时恰好进入与圆弧轨道底端相切的水平传送带,传送带由一电动机驱动着匀速向左转动,速度大小为v=3m/s.已知圆弧轨道半径R=0.8m,物块与传送带间的动摩擦因数为μ=0.1,两皮带轮之间的距离为L=10m,重力加速度g=10m/s2;求:
如图所示,一个可视为质点的物块,质量为m=2kg,从光滑四分之一圆弧轨道顶端由静止滑下,到达底端时恰好进入与圆弧轨道底端相切的水平传送带,传送带由一电动机驱动着匀速向左转动,速度大小为v=3m/s.已知圆弧轨道半径R=0.8m,物块与传送带间的动摩擦因数为μ=0.1,两皮带轮之间的距离为L=10m,重力加速度g=10m/s2;求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com