
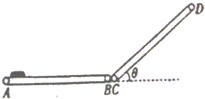
 如图是课外活动小组为某仓库设计的一个皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B两端相距3m,另一台倾斜,传送带与地面的倾角θ=37°,C、D两端相距4.45m,B、C相距很近,水平部分AB以5m/s的速率顺时针转动,将一工件轻放在A端,到达B端后,速度大小不变地传到倾斜的CD部分,工件与传送带间的动摩擦因数均为0.5,其最大静摩擦力认为等于滑动摩擦力(sin37°=0.6,cos37°=0.8,g取10m/s2).
如图是课外活动小组为某仓库设计的一个皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B两端相距3m,另一台倾斜,传送带与地面的倾角θ=37°,C、D两端相距4.45m,B、C相距很近,水平部分AB以5m/s的速率顺时针转动,将一工件轻放在A端,到达B端后,速度大小不变地传到倾斜的CD部分,工件与传送带间的动摩擦因数均为0.5,其最大静摩擦力认为等于滑动摩擦力(sin37°=0.6,cos37°=0.8,g取10m/s2).分析 (1)工件放上传送带先做匀加速直线运动,求出工件达到传送带速度所需的时间和位移,判断工件在整个过程中的运动,从而根据运动学规律求出工件沿传送带从A运动到B的时间.
(2)由牛顿第二定律可求得工件的加速度,因工件的最大速度只能为5m/s,则应判断工件到达B点时是否已达最大速度,若没达到,则由位移与速度的关系可求得B点速度,若达到,则以5m/s的速度冲上CD;在CD面上由牛顿第二定律可求得工件的加速度,则由位移和速度的关系可求得上升的最大距离;
(3)工件在CD上应做减速运动,若CD的速度较小,则工件的先减速到速度等于CD的速度,然后可能减小到零,此为最长时间;而若传送带的速度较大,则工件应一直减速,则可求得最短时间;
解答 解:(1)工件在传送带AB上,与之有相对滑动时μmg=ma1
a1=μg=0.5×10m/s2=5m/s2
达到共同速度所需时间为t1
v0=a1t1
t1=$\frac{{v}_{0}}{{a}_{1}}=\frac{5}{5}$s=1s
在1s内通过的位移为${s}_{1}=\frac{0+5}{2}×1m=2.5m$
故工件在AB传送带上先匀加速直线运动后做匀速直线运动速度v=v0=5m/s,匀速运动所需时间为.
${t}_{2}=\frac{{L}_{1}-{s}_{1}}{{v}_{0}}=\frac{3-2.5}{5}s=0.1s$
工件沿传送带从A运动到B的时间为
t=t1+t2=1s+0.1s=1.1s
(2)设工件在CD上运动的加速度大小为a,由牛顿第二定律得mgsinθ+μmgcosθ=ma
代入数据得 a2=10 m/s2
所以能滑上的最大距离 s=$\frac{{v}_{0}^{2}}{2{a}_{2}}$═1.25m
(3)设CD部分运转速度为v1时工件恰能到达D点(即工件到达D点时速度恰好为零),则工件速度减为v1之前的加速度为a3=-g(sinθ+μcosθ)=-10 m/s2
工件速度小于v1至减为零前的加速度为a4=-g(sinθ-μcosθ)=-2 m/s2
由$\frac{{v}_{1}^{2}{-v}_{0}^{2}}{2{a}_{3}}+\frac{0{-v}_{1}^{2}}{2{a}_{4}}=4.45$
代入数据,解得 v1=4m/s,即要把工件送到D点,CD部分的速度vCD≥v1=4m/s
工件恰能运到D点所用时间最长为tmax=$\frac{{v}_{1}-{v}_{0}}{{a}_{3}}+\frac{0-{v}_{1}}{{a}_{4}}=\frac{4-5}{-10}+\frac{0-4}{-2}s=2.1s$
若CD部分传送带的速度较大,使工件沿CD上滑时所受摩擦力一直沿皮带向上,
则所用时间最短,此种情况工件加速度一直为a4.
由SCD=v0tmin+$\frac{1}{2}$a4t2min,
代入数据得:tmin=1.16s
所以,所求的时间t的范围为 1.16 s≤t≤2.1 s;
答:(1)工件被传送到B点的速度大小为5m/s,从A到B所用的时间为1.1s;
(2)若CD 部分传送带不运转,工件沿传送带所能上升的最大距离为1.25m.
(3)若要工件能被送到D 端,CD 部分顺时针运转的速度应满足大于等于4m/s,工件从C 端到D 端所用时间的取值范围为1.16 s≤t≤2.1 s.
点评 本题难点在于通过分析题意找出临条界件,注意工件在CD段所可能做的运动情况,从而分析得出题目中的临界值为到达D点时速度恰好为零;本题的难度较大.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中物理 来源: 题型:选择题
| A. | $\frac{1}{2}$at2 | B. | at2 | C. | $\frac{3}{2}$at2 | D. | 2at2 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
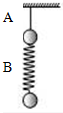 如图所示,用不可伸长的轻质细线和轻质弹簧分别竖直吊起质量相同的小球A、B,突然剪断轻绳的瞬间,A、B小球的加速度aA和aB分别为( )
如图所示,用不可伸长的轻质细线和轻质弹簧分别竖直吊起质量相同的小球A、B,突然剪断轻绳的瞬间,A、B小球的加速度aA和aB分别为( )| A. | aA=0,aB=g | B. | aA=g,aB=0 | C. | aA=0,aB=2g | D. | aA=2g,aB=0 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
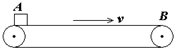 水平传送带以v=1.5m/s速度匀速运动,传送带AB两端距离为6.75m,将物体轻放在传送带的A端,它运动到传送带另一端B所需时间为6s,求:
水平传送带以v=1.5m/s速度匀速运动,传送带AB两端距离为6.75m,将物体轻放在传送带的A端,它运动到传送带另一端B所需时间为6s,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 有相同的速度 | |
| B. | 有相同的速率和动能 | |
| C. | 从抛出到着地,重力做的功相等,重力势能的减少相等 | |
| D. | 因为加速度均为g,故从抛出到着地,运动时间相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 物体的重力势增加$\frac{1}{5}$mgh | B. | 物体的动能增加$\frac{1}{5}$mgh | ||
| C. | 物体的机械能增加$\frac{1}{5}$mgh | D. | 物体的机械能增加$\frac{4}{5}$mgh |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com