
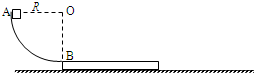
 ��ͼ��ʾ������ֱƽ�����а뾶ΪR�Ĺ⻬�ķ�֮һ Բ�ι������ߵ�A��Բ������ˮƽ���⻬ˮƽ�������㹻����ľ�壬����Ϊm0�������ǡ�ý���Բ����͵�B�����ھ�ֹ״̬��һ������Ϊm1������A���ɾ�ֹ��ʼ�»�������B�㻬��ľ�壬�����ľ��֮��Ķ�Ħ������Ϊ�̣�ͬʱľ���ܵ�ˮƽ���Һ���F=2��m1g�����ã��������ٶ�Ϊg����
��ͼ��ʾ������ֱƽ�����а뾶ΪR�Ĺ⻬�ķ�֮һ Բ�ι������ߵ�A��Բ������ˮƽ���⻬ˮƽ�������㹻����ľ�壬����Ϊm0�������ǡ�ý���Բ����͵�B�����ھ�ֹ״̬��һ������Ϊm1������A���ɾ�ֹ��ʼ�»�������B�㻬��ľ�壬�����ľ��֮��Ķ�Ħ������Ϊ�̣�ͬʱľ���ܵ�ˮƽ���Һ���F=2��m1g�����ã��������ٶ�Ϊg�������� ��1���ɻ�е���غ㶨�������鵽��B��ʱ���ٶȴ�С����龭��B��ʱ�����������֧�����ĺ����ṩ����������ţ�ٵڶ�����������������֧������
��2����黬��ľ��������������ȼ����˶�����ţ�ٵڶ����ɷֱ���������ľ��ļ��ٶȣ������˶�ѧ��ʽ�õ����ߵ��ٶȺ�λ����ʱ��Ĺ�ϵʽ���������ٶ����ʱ��������ľ�廬���ľ������������⣮
��3������������о���1�������ٶ���Ⱥ�һ���˶�����ţ�ٵڶ����ɶ�������һ���˶��ļ��ٶȣ��õ����ٶȵ��������������λ����������2�������ľ�����˻��£�������λ�ƣ�����������
��� �⣺��1�������Բ�����˶�ʱ���ɻ�е���غ�ã�
m1gR=$\frac{1}{2}{m}_{1}{v}_{0}^{2}$
�ɵã�v0=$\sqrt{2gR}$
��龭��B��ʱ����ţ�ٵڶ����ɵã�
N-m1g=m1$\frac{{v}_{0}^{2}}{R}$
��ã�N=3m1g
��2�������ľ���ϻ��������У���ţ�ٵڶ����ɺ��˶�ѧ��ʽ�ã�
����飺-��m1g=m1a1��a1=-��g����v0=$\sqrt{2gR}$
�ٶȣ�v1=v0+a1t=$\sqrt{2gR}$-��gt
λ�ƣ�x1=v0t+$\frac{1}{2}$a1t2=$\sqrt{2gR}$t-$\frac{1}{2}$��gt2��
��ľ�壺F+��m1g=m0a2��a2=$\frac{3��{m}_{1}g}{{m}_{0}}$
�ٶȣ�v2=a2t=$\frac{3��{m}_{1}g}{{m}_{0}}$t
λ�ƣ�x2=$\frac{1}{2}$a2t2=$\frac{3��{m}_{1}g}{2{m}_{0}}$t2��
��v1=v2ʱ��������ľ�����һ�����Զ�����ã�
$\sqrt{2gR}$-��gt=$\frac{3��{m}_{1}g}{{m}_{0}}$t
���� t=$\frac{{m}_{0}\sqrt{2gR}}{�̣�{m}_{0}+3{m}_{1}��g}$
��������ľ�廬�����������xmax=x1-x2=$\frac{{m}_{0}R}{�̣�{m}_{0}+3{m}_{1}��}$
��3���ٶ���ͬʱ���������һ���˶�������ٶ�Ϊa
�����壺a=$\frac{F}{{m}_{0}+{m}_{1}}$=$\frac{2{��m}_{1}g}{{m}_{0}+{m}_{1}}$
��a��|a1|����m0��m1ʱ�������ľ��һ�������˶������ٷ�����Ի����������������Ϊ
Q=��m1g��xmax=$\frac{{m}_{0}{m}_{1}gR}{{m}_{0}+3{m}_{1}}$
��a��|a1|����m0��m1ʱ�������ľ������Ի�����ľ���˶������죬��齫ľ������£������������Ϊ
Q=2��m1g��xmax=2$\frac{{m}_{0}{m}_{1}gR}{{m}_{0}+3{m}_{1}}$
�𣺣�1������B��ʱ�ܵ��ĵ�����3m1g��
��2��������ľ�廬������������$\frac{{m}_{0}R}{�̣�{m}_{0}+3{m}_{1}��}$��
��3������ľ���Ħ������������Ϊ$\frac{{m}_{0}{m}_{1}gR}{{m}_{0}+3{m}_{1}}$��2$\frac{{m}_{0}{m}_{1}gR}{{m}_{0}+3{m}_{1}}$��
���� ��������Ҫ��������ľ����������̣������ٶ��������ٽ�״̬�����������ܵ��˶�״̬�ǹؼ������ţ�ٵڶ����ɺ��˶�ѧ��ʽ���д�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��ABΪ��Ǧ�=37���б�����������AC���ֹ⻬��CB���ֲִڣ�BPΪԲ�Ľǵ���143�㣬�뾶R=1m����ֱ�⻬Բ���ι���������������B�㣬P��0������ͬһ��ֱ���ϣ��ᵯ��һ�˹̶���A�㣬��һ���ɶ���б����C�㴦������һ����m=2kg����������������½����ɻ���ѹ����D���˨�ӣ��ͷţ���龭��C���C���˶���B������е�λ����ʱ��Ĺ�ϵΪx=12t-4t2��ʽ��x��λ��m��t��λ��s������������һ�ξ���B���ǡ�ܵ���P�㣬��sin 37��=0.6��cos 37��=0.8��gȡ10m/s2������
��ͼ��ʾ��ABΪ��Ǧ�=37���б�����������AC���ֹ⻬��CB���ֲִڣ�BPΪԲ�Ľǵ���143�㣬�뾶R=1m����ֱ�⻬Բ���ι���������������B�㣬P��0������ͬһ��ֱ���ϣ��ᵯ��һ�˹̶���A�㣬��һ���ɶ���б����C�㴦������һ����m=2kg����������������½����ɻ���ѹ����D���˨�ӣ��ͷţ���龭��C���C���˶���B������е�λ����ʱ��Ĺ�ϵΪx=12t-4t2��ʽ��x��λ��m��t��λ��s������������һ�ξ���B���ǡ�ܵ���P�㣬��sin 37��=0.6��cos 37��=0.8��gȡ10m/s2�������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���������������˶�ʱ������Ե���û���������� | |
| B�� | �������˶������壬����ٶȷ���һ���DZ仯�� | |
| C�� | һ������������ϣ����������ϵĵ��������������鷢�����α� | |
| D�� | һ�������������������컨���ϣ����ݶ��������������Ե��ݵ�������һ���������ͷ������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | ͼ�ҽ�ͣ��P��ǰ��ij�� | B�� | ͼ����ͣ��P��ǰ��ij�� | ||
| C�� | ͼ�ҽ�ͣ��P�����ij�� | D�� | ͼ����ͣ��P�㴦 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���ݶ���ʽB=$\frac{F}{IL}$���ų���ij��ĴŸ�ǿ��B��F�����ȣ���IL�ɷ��� | |
| B�� | �Ÿ�ǿ��B��ʸ���������밲����F�ķ�����ͬ | |
| C�� | �Ÿ�ǿ��B��ʸ����������ͨ���õ�ĴŸ��ߵ����߷�����ͬ | |
| D�� | ��ȷ���Ĵų��У�ͬһ��ĴŸ�Ӧǿ����ȷ���ģ���ͬ��ĴŸ�Ӧǿ�ȿ��ܲ�ͬ���Ÿ����ܵĵط��Ÿ�Ӧǿ�ȴ�Щ���Ÿ�����ĵط��Ÿ�Ӧǿ��СЩ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
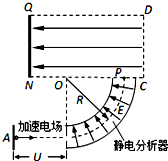 ��ͼ����ֹ��A�������ӣ������ٵ糡���ٺ���ͼ��Բ������ͨ���������������P�㴹ֱCN�������������н���ǿ�糡���糡����ˮƽ�����������ͨ�����о��ȷ���ֲ��ĵ糡����֪Բ�����ߵİ뾶ΪR�������ڴ���ǿΪE��������ͼ��ʾ����������Ϊm�������Ϊq��$\overline{ON}$=2d��$\overline{PN}$=3d�������������ƣ�
��ͼ����ֹ��A�������ӣ������ٵ糡���ٺ���ͼ��Բ������ͨ���������������P�㴹ֱCN�������������н���ǿ�糡���糡����ˮƽ�����������ͨ�����о��ȷ���ֲ��ĵ糡����֪Բ�����ߵİ뾶ΪR�������ڴ���ǿΪE��������ͼ��ʾ����������Ϊm�������Ϊq��$\overline{ON}$=2d��$\overline{PN}$=3d�������������ƣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com