
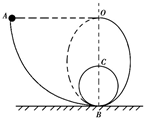
 如图所示,光滑轨道ABCBO在同一竖直平面内,AB段为半径为R的四分之一圆弧,圆心在O点,该圆弧与圆轨道BCB及半椭圆形轨道BO相切于B点,现让一质量为m的小球以向下的初速度v0从A点进入轨道,结果在C点对圆轨道的压力为F,在O点对轨道的压力恰好为零.
如图所示,光滑轨道ABCBO在同一竖直平面内,AB段为半径为R的四分之一圆弧,圆心在O点,该圆弧与圆轨道BCB及半椭圆形轨道BO相切于B点,现让一质量为m的小球以向下的初速度v0从A点进入轨道,结果在C点对圆轨道的压力为F,在O点对轨道的压力恰好为零.分析 (1)轨道是光滑的,从A点到C点,由机械能守恒定律列式.在C点,由合力提供向心力,由牛顿第二定律列式,联立可求圆轨道BCB的半径r1;
(2)根据机械能守恒可知,小球运动到O点时速度大小为v0,在O点,由重力充当向心力,由牛顿第二定律求椭圆轨道在O点的曲率半径r2;
(3)小球从O点抛出后做平抛运动,由平抛运动的规律求出O点的速度,在O点,由牛顿定律求小球在O点对轨道的压力.从A点到O点根据动能定理求克服摩擦力做功.
解答 解:(1)由于轨道是光滑的,从A点到C点,由机械能守恒定律有:
$\frac{1}{2}$m${v}_{0}^{2}$+mgR=2mgr1+$\frac{1}{2}$m${v}_{1}^{2}$
在C点,由牛顿第二定律有:
F+mg=m$\frac{{v}_{1}^{2}}{{r}_{1}}$
解得:r1=$\frac{m{v}_{0}^{2}+2mgR}{F+5mg}$
(2)根据机械能守恒定律可知,小球运动到O点时速度大小为v0.由于小球在O点对轨道的压力为零,有:
mg=m$\frac{{v}_{0}^{2}}{{r}_{2}}$
得:r2=$\frac{{v}_{0}^{2}}{g}$
(3)小球从O点抛出后做平抛运动,
水平方向有 $\frac{\sqrt{2}}{2}$R=v2't
竖直方向有 $\frac{\sqrt{2}}{2}$R=$\frac{1}{2}$gt2
在O点,由牛顿第二定律有:F'+mg=m$\frac{{v}_{2}{'}^{2}}{{r}_{2}}$
解得:F'=($\frac{\sqrt{2}gR}{4{v}_{0}^{2}}$-1)mg
所以由牛顿第三定律得小球对轨道的压力为:F=F'=($\frac{\sqrt{2}gR}{4{v}_{0}^{2}}$-1)mg
从A点到O点根据动能定理有:
W=$\frac{1}{2}$m(2v0)2-$\frac{1}{2}$mv2'2
解得:W=2m${v}_{0}^{2}$-$\frac{\sqrt{2}mgR}{8}$
答:(1)圆轨道BCB的半径r1是$\frac{m{v}_{0}^{2}+2mgR}{F+5mg}$.
(2)椭圆轨道在O点的曲率半径r2是$\frac{{v}_{0}^{2}}{g}$.
(3)小球在O点对轨道的压力为($\frac{\sqrt{2}gR}{4{v}_{0}^{2}}$-1)mg,此过程克服摩擦力做功为2m${v}_{0}^{2}$-$\frac{\sqrt{2}mgR}{8}$.
点评 本题要认真分析物体的运动过程和状态,在圆轨道和椭圆上某一状态,运用牛顿定律研究.两个状态之间速度的关系运用动能定理或机械能守恒定律研究.


 考前必练系列答案
考前必练系列答案科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
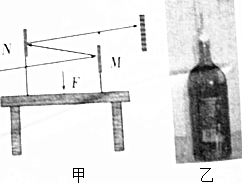 为了演示“力作用在物体上能产生微小形变”,老师做了如下两个实验:如图甲所示,在一张大桌子上放两个平面镜,让一束光依次被M和N两平面镜反射,最后射到墙上,形成一个光点,当用力压桌面时,观察墙上光点位置的变化;如图乙所示,在底部为椭圆的扁玻璃瓶中盛满红墨水,用插有细玻璃的橡皮擦封口,使水面位于细管中,当用手捏玻璃瓶时,观察细管中的水面变化.下列说法中正确的是( )
为了演示“力作用在物体上能产生微小形变”,老师做了如下两个实验:如图甲所示,在一张大桌子上放两个平面镜,让一束光依次被M和N两平面镜反射,最后射到墙上,形成一个光点,当用力压桌面时,观察墙上光点位置的变化;如图乙所示,在底部为椭圆的扁玻璃瓶中盛满红墨水,用插有细玻璃的橡皮擦封口,使水面位于细管中,当用手捏玻璃瓶时,观察细管中的水面变化.下列说法中正确的是( )| A. | 图甲中减小对桌面的压力,墙上光点上移 | |
| B. | 图甲中增大对桌面的压力,墙上光点上移 | |
| C. | 图乙中用手沿瓶长轴方向紧捏时,管中的液面会上升 | |
| D. | 图乙中用手沿瓶短轴方向紧捏时,管中的液面会下降 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
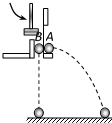 用如图所示的装置研究平抛运动,用小锤打击弹性金属片后,A球沿水平方向抛出,同时B球被松开,自由下落.A、B两球同时开始运动,多次改变打击的力度,重复这个实验,观察到两球同时落地(填“同时”或“不同时”).此实验证明平抛运动在竖直方向上的分运动是自由落体运动.(填“匀速直线运动”或“自由落体运动”)
用如图所示的装置研究平抛运动,用小锤打击弹性金属片后,A球沿水平方向抛出,同时B球被松开,自由下落.A、B两球同时开始运动,多次改变打击的力度,重复这个实验,观察到两球同时落地(填“同时”或“不同时”).此实验证明平抛运动在竖直方向上的分运动是自由落体运动.(填“匀速直线运动”或“自由落体运动”)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
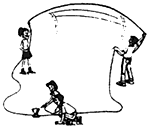 如图所示,操场上两同学用铜芯电缆线做摇绳发电实验,他们观察到灵敏电流计的指针发生了偏转,关于摇绳发电产生的电流,下列说法正确的是( )
如图所示,操场上两同学用铜芯电缆线做摇绳发电实验,他们观察到灵敏电流计的指针发生了偏转,关于摇绳发电产生的电流,下列说法正确的是( )| A. | 仅增大绳的长度,灵敏电流计中电流的最大值不变 | |
| B. | 仅增大摇绳频率,灵敏电流计中电流的最大值增大 | |
| C. | 灵敏电流计中电流大小与两同学的站立方向无关 | |
| D. | 匀速率摇动绳子时,流过灵敏电流计的是大小变化的直流电 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com