
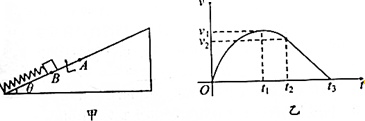
分析 (1)t2-t3间的图象是一条直线,说明物块向上做匀减速直线运动,由速度公式即可求出加速度,然后结合受力分析即可求出动摩擦因数;
(2)0-t2时间内弹簧做的功转化为物块的动能与势能,结合功能关系即可求出弹簧被压缩时具有的最大弹性势能Eρ;
(3)由功能关系求出在t1时刻弹簧的弹性势能,结合功能关系即可求出0-t1时间内弹簧的弹力做的功W.
解答 解:(1)由图可知,t2-t3间物块向上做匀减速直线运动,则加速度:
a=$\frac{△v}{△t}=\frac{0-{v}_{2}}{{t}_{3}-{t}_{2}}$
t2-t3间物块向上做匀减速直线运动,物块的加速度不变,则物块只受到重力、支持力和摩擦力的作用,沿斜面方向:
ma=-mgsinθ-μmgcosθ
联立得:μ=$\frac{gsinθ-\frac{{v}_{2}}{{t}_{3}-{t}_{2}}}{gcosθ}$
(2)结合以上的分析可知,在t2时刻物块开始做匀减速直线运动,说明t2时刻物块恰好到达A点,0-t2时间内弹簧的弹性势能恰好都转化为物块的动能、重力势能和内能,则:
${E}_{P}=mgLsinθ+\frac{1}{2}m{v}_{2}^{2}$+μmgcosθ•L=$2mgLsinθ+\frac{1}{2}m{v}_{2}^{2}-\frac{m{v}_{2}L}{{t}_{3}-{t}_{2}}$
(3)由图可知,在t1时刻物块的速度最大,可知在t1时刻物块受到的合外力恰好为0,即:
k△x=mgsinθ+μmgcosθ
t1-t2时间内只有重力、弹簧的弹力和摩擦力做功,由功能关系可得:
${E}_{P}′+\frac{1}{2}m{v}_{1}^{2}=mg△x•sinθ+\frac{1}{2}m{v}_{2}^{2}$+μmgcosθ•△x
0-t1时间内弹簧的弹力做的功等于弹簧减少的弹性势能,即:
W=△EP=EP-EP′
联立得:W=$2mgLsinθ+\frac{1}{2}m{v}_{1}^{2}-\frac{m{v}_{2}L}{{t}_{3}-{t}_{2}}$$-\frac{{m}^{2}{g}^{2}}{k}(2sinθ-\frac{{v}_{2}}{{t}_{3}-{t}_{2}})^{2}$
答:(1)物块与斜面间的动摩擦因数μ是$\frac{gsinθ-\frac{{v}_{2}}{{t}_{3}-{t}_{2}}}{gcosθ}$;
(2)弹簧被压缩时具有的最大弹性势能是$2mgLsinθ+\frac{1}{2}m{v}_{2}^{2}-\frac{m{v}_{2}L}{{t}_{3}-{t}_{2}}$;
(3)0-t1时间内弹簧的弹力做的功W是$2mgLsinθ+\frac{1}{2}m{v}_{1}^{2}-\frac{m{v}_{2}L}{{t}_{3}-{t}_{2}}$$-\frac{{m}^{2}{g}^{2}}{k}(2sinθ-\frac{{v}_{2}}{{t}_{3}-{t}_{2}})^{2}$.
点评 本题考查了牛顿第二定律、动能定理和运动学公式的综合运用,关键结合图象理清滑块在整个过程中的运动规律,结合牛顿第二定律和运动学公式综合求解.


科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 同一物体运动速度大比速度小时难以停下来,所以物体运动速度大时具有较大的惯性 | |
| B. | 同一物体不论受力的大小以及力的变化情况如何,也不论速度大小及运动状态如何变化,惯性是恒定不变的 | |
| C. | 不同物体比较,体积越大,惯性越大 | |
| D. | 不同物体比较,质量越大,惯性越大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
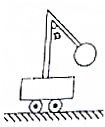 如图所示,小车上固定一弯折硬杆ABC,C端固定一质量为m的小球,已知a角恒定.当小车以加速度a水平向左做匀加速直线运动时,BC杆对小球的作用力大小和方向.
如图所示,小车上固定一弯折硬杆ABC,C端固定一质量为m的小球,已知a角恒定.当小车以加速度a水平向左做匀加速直线运动时,BC杆对小球的作用力大小和方向.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
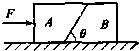 如图所示,两光滑的梯形木块A和B,紧靠放在光滑水平面上,已知θ=60°,mA=2kg,mB=1kg,现同时施水平力F,使两木块使向右加速运动,要使两木块在运动过程中无相对滑动,则F的最大值多大?
如图所示,两光滑的梯形木块A和B,紧靠放在光滑水平面上,已知θ=60°,mA=2kg,mB=1kg,现同时施水平力F,使两木块使向右加速运动,要使两木块在运动过程中无相对滑动,则F的最大值多大?查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 在如图所示的电路中,电源电动势E=9V、内阻r=1Ω、电阻R2=8Ω、灯A标有“6V 6W”字样,灯B标有“4V 4W”字样,如果要使灯A正常发光(设灯丝电阻不变),求:
在如图所示的电路中,电源电动势E=9V、内阻r=1Ω、电阻R2=8Ω、灯A标有“6V 6W”字样,灯B标有“4V 4W”字样,如果要使灯A正常发光(设灯丝电阻不变),求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 如图所示,AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,一小球自A点由静止开始沿轨道下滑,已知圆轨道半径为R,小球到达B点时的速度为v,则小球在B点受2个力的作用,这几个力的合力的方向是竖直向上,小球在B点的加速度大小为$\frac{{v}^{2}}{R}$,方向是竖直向上.(不计一切阻力)
如图所示,AB是竖直平面内的四分之一圆弧轨道,在下端B与水平直轨道相切,一小球自A点由静止开始沿轨道下滑,已知圆轨道半径为R,小球到达B点时的速度为v,则小球在B点受2个力的作用,这几个力的合力的方向是竖直向上,小球在B点的加速度大小为$\frac{{v}^{2}}{R}$,方向是竖直向上.(不计一切阻力)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
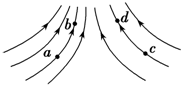
| A. | c点的电场强度大于b点的电场强度 | B. | c点的电场强度小于b点的电场强度 | ||
| C. | b点的电场强度小于d点的电场强度 | D. | a点和b点的电场强度的方向相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
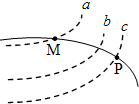 如图所示,虚线a、b、c代表电场中的三个等差等势面,ab的间距大于bc的间距.实线为一带电的粒子仅在电场力作用下通过该区域时的运动轨迹,P、M为轨迹上的两个点,由此可知( )
如图所示,虚线a、b、c代表电场中的三个等差等势面,ab的间距大于bc的间距.实线为一带电的粒子仅在电场力作用下通过该区域时的运动轨迹,P、M为轨迹上的两个点,由此可知( )| A. | 粒子在M点受到的电场力比在P点受到的电场力大 | |
| B. | 粒子在P、M两点间的运动过程,电场力一定做正功 | |
| C. | 粒子在M点的电势能一定比在P点的电势能大 | |
| D. | 三个等势面中,a的电势一定最高 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com