
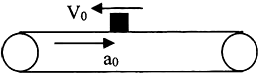
 一水平浅色足够长传送带,t=0时刻由静止开始以恒定的加速度a0向右运动,当其速度达到V0后,便以此速度做匀速运动,t=0时刻,一质量为m的煤块(可视为质点)在大小为V0的初速度水平向左抛到传送带上中间某处,经过一段时间,煤块在传送带上留下一段黑色的痕迹后,煤块相对传送带不再滑动,已知煤块与传送带之间动摩擦因数为μ,求:
一水平浅色足够长传送带,t=0时刻由静止开始以恒定的加速度a0向右运动,当其速度达到V0后,便以此速度做匀速运动,t=0时刻,一质量为m的煤块(可视为质点)在大小为V0的初速度水平向左抛到传送带上中间某处,经过一段时间,煤块在传送带上留下一段黑色的痕迹后,煤块相对传送带不再滑动,已知煤块与传送带之间动摩擦因数为μ,求:分析 (1)煤块在滑动摩擦力作用下向左做匀减速运动,速度为零时到达最左端,由动能定理求煤块水平向左运动的最大位移.
(2)煤块与传送带刚好相对静止时两者速度相同,由动能定理求传送带对煤块做的功W.
(3)由牛顿第二定律和运动学公式速度公式、位移公式结合求出煤块与传送带的相对位移,即为黑色痕迹的长度.
解答 解:(1)设煤块水平向左运动的最大位移为x.
根据动能定理得
-μmgx=0-$\frac{1}{2}m{v}_{0}^{2}$
可得 x=$\frac{{v}_{0}^{2}}{2μg}$
(2)、(3)在煤块向左运动的过程中:
煤块向左匀减速运动的加速度大小为 a=$\frac{μmg}{m}$=μ
向左运动的时间为 t1=$\frac{{v}_{0}}{μg}$
若a0t1≤v0,则煤块与传送带间的相对位移大小为△x1=x+$\frac{1}{2}{a}_{0}{t}_{1}^{2}$=$\frac{{v}_{0}^{2}(μg+{a}_{0})}{2{μ}^{2}{g}^{2}}$
若a0t1>v0,煤块与传送带间的相对位移大小为△x2=x+[$\frac{{v}_{0}^{2}}{2{a}_{0}}$+v0(t1-$\frac{{v}_{0}}{{a}_{0}}$)]=$\frac{3{v}_{0}^{2}}{2μg}$-$\frac{{v}_{0}^{2}}{2{a}_{0}}$;
在煤块向右运动的过程中:
设煤块向右加速经历时间t2后速度与传送带相同.则有
at2=a0(t1+t2)
可能有两种情况:
1、若a0t1>v0,煤块向右运动时传送带已经以速度v0匀速运动,at2=v0,解得 t2=$\frac{{v}_{0}}{a}$=$\frac{{v}_{0}}{μg}$,
煤块与传送带间的相对位移大小为△x3=v0t2-$\frac{{v}_{0}}{2}{t}_{2}$=$\frac{{v}_{0}^{2}}{2μg}$
故黑色痕迹的长度为△xⅠ=△x2+△x3=$\frac{2{v}_{0}^{2}}{μg}$-$\frac{{v}_{0}^{2}}{2{a}_{0}}$;
传送带对煤块做的功 W=$\frac{1}{2}m{v}_{0}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$=0
2、若a0t1≤v0,又有两种情况:
①煤块与传送带相对静止时,煤块的速度小于v0,由 at2=a0(t1+t2)得:
t2=$\frac{{a}_{0}{v}_{0}}{μg(μg-{a}_{0})}$
传送带与煤块共同速度 v=$\frac{{a}_{0}{v}_{0}}{μg-{a}_{0}}$
煤块与传送带间的相对位移大小为△x5=v0t2-$\frac{{v}_{0}}{2}{t}_{2}$=$\frac{{v}_{0}^{2}}{2μg}$-$\frac{{a}_{0}{v}_{0}^{2}}{2(μg-{a}_{0})}$
故黑色痕迹的长度为△xⅡ=△x1+△x5=$\frac{{v}_{0}^{2}(μg+{a}_{0})}{2{μ}^{2}{g}^{2}}$+($\frac{{v}_{0}^{2}}{2μg}$-$\frac{{a}_{0}{v}_{0}^{2}}{2(μg-{a}_{0})}$)
传送带对煤块做的功 W=$\frac{1}{2}m{v}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$=$\frac{m{v}_{0}^{2}(2μg{a}_{0}-{μ}^{2}{g}^{2})}{2(μg-{a}_{0})^{2}}$
②煤块与传送带相对静止时,煤块的速度等于v0,则
煤块与传送带间的相对位移大小为△x3=v0t2-$\frac{{v}_{0}}{2}{t}_{2}$=$\frac{{v}_{0}^{2}}{2μg}$
故黑色痕迹的长度为△xⅢ=△x1+△x3=$\frac{2{v}_{0}^{2}}{μg}$-$\frac{{v}_{0}^{2}}{2{a}_{0}}$;
传送带对煤块做的功 W=$\frac{1}{2}m{v}_{0}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$=0
答:
(1)取地面为参考系,煤块水平向左运动的最大位移为$\frac{{v}_{0}^{2}}{2μg}$;
(2)从煤块抛上传送带到煤块与传送带刚好相对静止的过程中,传送带对煤块做的功W为0或$\frac{m{v}_{0}^{2}(2μg{a}_{0}-{μ}^{2}{g}^{2})}{2(μg-{a}_{0})^{2}}$;
(3)黑色痕迹的长度可能为$\frac{2{v}_{0}^{2}}{μg}$-$\frac{{v}_{0}^{2}}{2{a}_{0}}$或[$\frac{{v}_{0}^{2}(μg+{a}_{0})}{2{μ}^{2}{g}^{2}}$+($\frac{{v}_{0}^{2}}{2μg}$-$\frac{{a}_{0}{v}_{0}^{2}}{2(μg-{a}_{0})}$)].
点评 本题的关键要煤块可能的运动情况,知道黑色痕迹的长度等于煤块与传送带间的相对位移的大小,由动能定理和牛顿运动定律、运动学公式结合研究.


科目:高中物理 来源:2016-2017学年山东济南一中高二理上学期期中考物理试卷(解析版) 题型:选择题
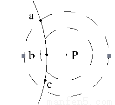
如图所示,P是固定的点电荷,虚线是以P为圆心的两个圆。带电粒子Q在P的电场中运动,运动轨迹与两圆在同一平面内,a、b、c为轨迹上的三个点。若Q仅受P的电场力作用,其在a、b、c点的加速度大小分别为aa、ab、ac,速度大小分别为va、vb、vc,则( )
A.aa>ab>ac,va>vc>vb
B.aa>ab>ac,vb>vc>va
C.ab>ac>aa,vb>vc>va
D.ab>ac>aa,va>vc>vb
查看答案和解析>>
科目:高中物理 来源:2016-2017学年江苏泰州中学高二上学期期中模拟物理试卷(解析版) 题型:选择题
A、B两个质点分别做匀速圆周运动,在相等时间内通过的弧长之比 ,转过的圆心角之比
,转过的圆心角之比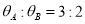 ,则下列说法中正确的是
,则下列说法中正确的是
A.它们的线速度之比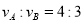
B.它们的角速度之比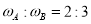
C.它们的周期之比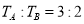
D.它们的向心加速度之比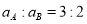
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,一带电粒子由O点垂直场强方向进入偏转电场,若初动能为Ek,射出电场时动能为2Ek,若初动能为4Ek,则射出电场时动能为(不计重力)( )
如图所示,一带电粒子由O点垂直场强方向进入偏转电场,若初动能为Ek,射出电场时动能为2Ek,若初动能为4Ek,则射出电场时动能为(不计重力)( )| A. | 3Ek | B. | 8Ek | C. | 4.25Ek | D. | 2.5Ek |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
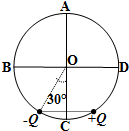 如图所示,AC、BD为圆的两条互相垂直的直径,圆心为O,半径为R,将电量均为Q的两个异种点电荷放在圆周上,它们的位置关于AC对称,且与O点的连线和OC间夹角各为30°,下列说法正确的是( )
如图所示,AC、BD为圆的两条互相垂直的直径,圆心为O,半径为R,将电量均为Q的两个异种点电荷放在圆周上,它们的位置关于AC对称,且与O点的连线和OC间夹角各为30°,下列说法正确的是( )| A. | 电子沿竖直方向从A点运动到C点,电场力做功为零 | |
| B. | 电子沿水平方向从B点运动到D点,电势能先减小后增大 | |
| C. | O点的场强大小为$\frac{kQ}{{R}^{2}}$ | |
| D. | O点的场强大小为$\frac{\sqrt{3}kQ}{{R}^{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
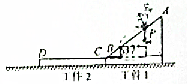 如图所示,质量为m1=0.6kg的工件1与质量为m2=0.2kg的工件2靠在一起(并不连接)置于粗糙的水平面上,工件1的上表面AB是一倾角为θ=37°的光滑斜面;工件2的上表面CD为一长度L=0.5m的粗糙水平面,CD与AB相较于B(C)点且与B在同一水平面上,两工件位于同一竖直平面内,与水平地面间的摩擦动因数为μ1=0.5,P为AB上的一个确定点,质量m+0.2kg,可视为质点的物块与CD间的动摩擦因数为μ2=0.4,回答下列问题:(取g=10m/s2,sin37°=0.6)
如图所示,质量为m1=0.6kg的工件1与质量为m2=0.2kg的工件2靠在一起(并不连接)置于粗糙的水平面上,工件1的上表面AB是一倾角为θ=37°的光滑斜面;工件2的上表面CD为一长度L=0.5m的粗糙水平面,CD与AB相较于B(C)点且与B在同一水平面上,两工件位于同一竖直平面内,与水平地面间的摩擦动因数为μ1=0.5,P为AB上的一个确定点,质量m+0.2kg,可视为质点的物块与CD间的动摩擦因数为μ2=0.4,回答下列问题:(取g=10m/s2,sin37°=0.6)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 丙椎着小车以0.5m/s的速度向右匀速运动 | |
| B. | 丙拉着小车以0.5m/s的速度向右匀速运动 | |
| C. | 丙推着小车以0.5m/s的速度向左匀速运动 | |
| D. | 丙推着小车由静止开始向左运动的瞬间 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 割刀运动的轨迹是一段直线 | |
| B. | 割刀完成一次切割的时间为10s | |
| C. | 割刀运动的实际速度为0.05$\sqrt{7}$m/s | |
| D. | 割刀完成一次切割的时间内,玻璃板的位移是1.5m |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com