
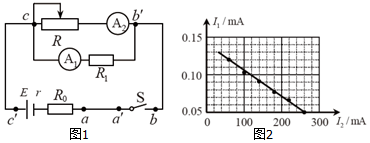
���� ͨ�����õ���ĵ�ѹʾ���Ƿ�Ϊ�㣬��ϵ�·����ȷ���ĸ����߶Ͽ���
���ݱպϵ�·ŷķ�����Լ���������·���ص㣬�ó��������ı���ʽ�����ͼ�ߵ�б�ʺͽؾ�����綯�ƺ�����Ĵ�С��
��� �⣺�ٽ��罨S�պϣ��ö��õ���ĵ�ѹ���Ȳ���a��b����ѹ��������Ϊ�㣬��֪cc�䲻�Ͽ����ٲ���a��a����ѹ����������Ϊ�㣬��֪bb��䲻�Ͽ�����һ����aa���Ͽ�����aa����ѹΪ�㣬��bb���߶Ͽ���
�ڸ��ݴ�������·���ص㣬��ϱպϵ�·ŷķ���ɵã�E=U+Ir��
����E=I1��R1+r1��+��I1+I2����R0+r����
��֪I1=$-\frac{{I}_{2}��r+3��}{1{0}^{4}}+\frac{E}{1{0}^{4}}$������ؾ�$\frac{E}{1{0}^{4}}=0.14��1{0}^{-3}$
��ã�E=1.4V��
ͼ��б�ʵľ���ֵΪ��$\frac{r+3}{1{0}^{4}}=\frac{��0.14-0.05����1{0}^{-3}}{260��1{0}^{-3}}$�����r��0.5����
�ʴ�Ϊ����aa'��bb'����1.4��1.36��1.44���ɣ� 0.5��0.4��0.6���ɣ�
���� �������Ĺؼ�ȷ�����ϵķ���������ͼ�����⣬һ��Ľ���˼·�ǵó���������֮��Ĺ�ϵʽ�����ͼ��б�ʺͽؾ������⣬�Ѷ��еȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{{k^2}-1}}}{k}$ | B�� | $\frac{{\sqrt{{k^2}+1}}}{k}$ | C�� | $\frac{k}{{\sqrt{{k^2}-1}}}$ | D�� | $\frac{1}{{\sqrt{1-{k^2}}}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
| A1 |
| A1 |
| A1 |
| A1 |
| A1 |
| A1 |
| A1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
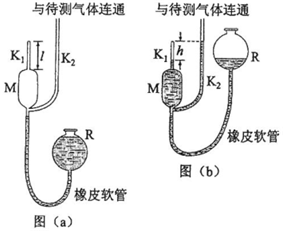 һ�ֲ���ϡ������ѹǿ��������ͼ��a����ʾ��������M���϶˺��¶˷ֱ���ͨ����ֱ����ϸ��K1��K2��K1��Ϊl�����˷�գ�K2�϶������������ͨ��M�¶˾���Ƥ���������ˮ��������R��ͨ����ʼ����ʱ��M��K2��ͨ��������R��ֱ��K2��ˮ������K1���˵ȸߣ���ʱˮ���ѽ���K1����K1��ˮ����ȶ��˵�h����ͼ��b����ʾ��������������¶ȡ���K2��ͨ�Ĵ��������ѹǿ�����ֲ��䣮��֪K1��K2���ھ���Ϊd��M���ݻ�ΪV0��ˮ�����ܶ�Ϊ�ѣ��������ٶȴ�СΪg����
һ�ֲ���ϡ������ѹǿ��������ͼ��a����ʾ��������M���϶˺��¶˷ֱ���ͨ����ֱ����ϸ��K1��K2��K1��Ϊl�����˷�գ�K2�϶������������ͨ��M�¶˾���Ƥ���������ˮ��������R��ͨ����ʼ����ʱ��M��K2��ͨ��������R��ֱ��K2��ˮ������K1���˵ȸߣ���ʱˮ���ѽ���K1����K1��ˮ����ȶ��˵�h����ͼ��b����ʾ��������������¶ȡ���K2��ͨ�Ĵ��������ѹǿ�����ֲ��䣮��֪K1��K2���ھ���Ϊd��M���ݻ�ΪV0��ˮ�����ܶ�Ϊ�ѣ��������ٶȴ�СΪg�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ����ǿ�ų��У�һ��100�ѵıպϾ��ν�����Ȧ������Ÿ��ߴ�ֱ�Ĺ̶�������ת������������Ȧ�Ĵ�ͨ����ʱ�䰴ͼʾ���ҹ��ɱ仯������Ȧ�ܵ���Ϊ2����������
����ǿ�ų��У�һ��100�ѵıպϾ��ν�����Ȧ������Ÿ��ߴ�ֱ�Ĺ̶�������ת������������Ȧ�Ĵ�ͨ����ʱ�䰴ͼʾ���ҹ��ɱ仯������Ȧ�ܵ���Ϊ2����������| A�� | t=0ʱ����Ȧƽ��ƽ���ڴŸ��� | |
| B�� | t=1sʱ����Ȧ�еĵ����ı䷽�� | |
| C�� | t=1.5 sʱ����Ȧ�еĸ�Ӧ�綯����� | |
| D�� | һ�������ڣ���Ȧ����������Ϊ8��2J |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
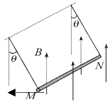 ����ֱ���ϵ���ǿ�ų��У��Ÿ�Ӧǿ�ȴ�СΪB����ʼʱϸ����ֱ���������ͨ���ɺ㶨��������������͵㿪ʼ���Ұڶ�������֪ϸ������ֱ�������н�Ϊ60����ͼ��ʾ������е���Ϊ��������
����ֱ���ϵ���ǿ�ų��У��Ÿ�Ӧǿ�ȴ�СΪB����ʼʱϸ����ֱ���������ͨ���ɺ㶨��������������͵㿪ʼ���Ұڶ�������֪ϸ������ֱ�������н�Ϊ60����ͼ��ʾ������е���Ϊ��������| A�� | ������M��N����СΪ$\frac{\sqrt{3}mg}{3Bl}$ | B�� | ������N��M����СΪ$\frac{\sqrt{3}mg}{3Bl}$ | ||
| C�� | ������M��N����СΪ$\frac{\sqrt{3}mg}{Bl}$ | D�� | ������N��M����СΪ$\frac{\sqrt{3}mg}{Bl}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
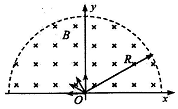 ��ͼ��ʾ����xOyƽ���ڣ���һ��OΪԲ�ġ�RΪ�뾶�İ�Բ����ǿ�ų����ų�����ֱ����ƽ������Ÿ�Ӧǿ�ȴ�СΪB��λ��O�������Դ��ڶ������ڵĸ������������������ͬ�ִ������ӣ����Ӿ�����Ӵų���Բ���߽���������ӵ�������ȣ�����Ϊm�������Ϊq��q��0�����������������Ӽ������þ����ƣ�
��ͼ��ʾ����xOyƽ���ڣ���һ��OΪԲ�ġ�RΪ�뾶�İ�Բ����ǿ�ų����ų�����ֱ����ƽ������Ÿ�Ӧǿ�ȴ�СΪB��λ��O�������Դ��ڶ������ڵĸ������������������ͬ�ִ������ӣ����Ӿ�����Ӵų���Բ���߽���������ӵ�������ȣ�����Ϊm�������Ϊq��q��0�����������������Ӽ������þ����ƣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
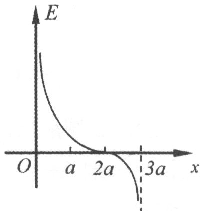 ��������Ϊ3a����������M��N���ֱ�̶���x����x1=0��x2=3a�������ϣ������������ϸ��㳡ǿE��x�仯��ϵ��ͼ��ʾ�������ж���ȷ���ǣ�������
��������Ϊ3a����������M��N���ֱ�̶���x����x1=0��x2=3a�������ϣ������������ϸ��㳡ǿE��x�仯��ϵ��ͼ��ʾ�������ж���ȷ���ǣ�������| A�� | ����M��Nһ��Ϊ���ֵ�� | |
| B�� | ����M��Nһ��Ϊͬ�ֵ�� | |
| C�� | ����M��N����������ľ���ֵ֮��Ϊ2��1 | |
| D�� | ��һ����������x���0.5a�ƶ���2.5a���õ�ɵĵ������ȼ�С������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
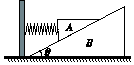 ��ͼ��ʾ����һ��Ǧ�=30���б����B������ΪM������A����Ϊm�����ɶ�����Aʩ��һ��ʼ�ձ���ˮƽ��������������A��B�ϵ�λ�ã�Aʼ���ܺ�B���־�ֹ���Դ˹�������˵����ȷ���ǣ�������
��ͼ��ʾ����һ��Ǧ�=30���б����B������ΪM������A����Ϊm�����ɶ�����Aʩ��һ��ʼ�ձ���ˮƽ��������������A��B�ϵ�λ�ã�Aʼ���ܺ�B���־�ֹ���Դ˹�������˵����ȷ���ǣ�������| A�� | A��B֮��ĽӴ�������ǹ⻬�� | |
| B�� | ���ɵ���Խ��A��B֮���Ħ����Խ�� | |
| C�� | A��B֮���Ħ����Ϊ0ʱ�����ɵ���Ϊ$\frac{\sqrt{3}}{3}$mg | |
| D�� | ���ɵ���Ϊ$\frac{\sqrt{3}}{2}$mgʱ��A����Ħ������СΪ$\frac{1}{4}$mg |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com