
 �ڹ⻬��Ե��ˮƽ���ϣ���x��0��d��Χ�ڴ��ڵ糡��ͼ��δ���������糡�ķ�����x�������ҵ糡ǿ�ȴ�СE��x�ķֲ���ͼ��ʾ����һ����Ϊm1������Ϊ+q��С��A����O���ɾ�ֹ�ͷţ���С��A�뿪�糡����һ����ֹ�Ҳ����磬����Ϊm2��С��B������ײ������ײ��������е����ʧ��С��A��B��С��ͬ����ײ�����е�ɲ�����ת�ƣ���
�ڹ⻬��Ե��ˮƽ���ϣ���x��0��d��Χ�ڴ��ڵ糡��ͼ��δ���������糡�ķ�����x�������ҵ糡ǿ�ȴ�СE��x�ķֲ���ͼ��ʾ����һ����Ϊm1������Ϊ+q��С��A����O���ɾ�ֹ�ͷţ���С��A�뿪�糡����һ����ֹ�Ҳ����磬����Ϊm2��С��B������ײ������ײ��������е����ʧ��С��A��B��С��ͬ����ײ�����е�ɲ�����ת�ƣ������� ��1������ţ�ٵڶ����������ٶȣ�
��2��ͼ����X��Χ��������������ʾ�������ݵ糡���������ڵ����ܵı仯����⣻
��3��ABϵͳ�����غ㣬���ݶ����غ㶨�ɺ������غ㶨����ʽ�����ܷ����ڶ�����ײӦ������ײ��A�ٶȴ�С����B���ٶȴ�С��
��� �⣺��1��С����0.5d���ܵ糡��Ϊ��F=$\frac{1}{2}{E}_{0}q$
����ţ������Ϊ��F=ma
�ã�$a=\frac{{{E_0}q}}{2m}$
��2��a��ͼ����X��Χ��������������ʾ������
W=$\frac{1}{2}$E0qd
b����С���˶�����X0=0��λ��ΪX
���ڵ����ܱ仯��Ϊ����Ep=-W
С����0��ĵ�����Ϊ0�����˶���X���ĵ�����${E}_{P}=-W=\frac{1}{2}\frac{{E}_{0}xq}{d}x$
����${E}_{P}=-\frac{{E}_{0}{x}^{2}q}{2d}$
��3��ABϵͳ�����غ㣬��A�ij��ٶȷ���Ϊ�������ݶ����غ㶨�ɵã�
m1v0=m1vA��+m2vB��
����ϵͳ�����غ�ã�
$\frac{1}{2}{m}_{1}{{v}_{0}}^{2}=\frac{1}{2}{m}_{1}{v}_{A}{��}^{2}+\frac{1}{2}{m}_{2}{v}_{B}{��}^{2}$
��ã�${v}_{A}��=\frac{{m}_{1}-{m}_{2}}{{m}_{1}+{m}_{2}}v$��${v}_{B}��=\frac{{2m}_{1}}{{m}_{1}+{m}_{2}}v$
���ܷ����ڶ�����ײӦ����|VA��|��VB��
��ã�m2-m1��2m1
����$\frac{{m}_{2}}{{m}_{1}}��3$
�𣺣�1����С��A�˶���0.5dʱ�ļ��ٶ�a�Ĵ�СΪ$\frac{{E}_{0}q}{2m}$��
��2��a������o��d�Ĺ����У��糡��С��A�����Ĺ�Ϊ$\frac{1}{2}$E0qd��
b����x=0������Ϊ0�����Ƶ�С��A������EP�ı���ʽΪ${E}_{P}=-\frac{{E}_{0}{x}^{2}q}{2d}$��
��3��Ϊʹ�ʵ�A�뿪�糡�����ʵ�B�ܷ����ڶ�����ײ���ʵ�A���ʵ�B������Ӧ����$\frac{{m}_{2}}{{m}_{1}}��3$��
���� ������Ҫ������ţ�ٵڶ����ɡ��糡��������ʽ�������غ㶨���Լ������غ㶨�ɵ�ֱ��Ӧ�ã�Ҫ��ͬѧ������ȷ�������⣬������Ŀ�ó���Ч��Ϣ��ע��ʹ�ö����غ㶨�ɽ���ʱҪ�涨������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���˹�ʽ�ۢݢ� | B�� | ���˹�ʽ�ܢݢ� | ||
| C�� | ���˹�ʽ�ܢ� | D�� | �������й�ʽ��������Լ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ����Ħ������ת��Ϊ���ܵĹ��̲����� | |
| B�� | �ӵ�һ��Դ����������������������ȫ��Ϊ����������Դ��� | |
| C�� | ����ֻ�ܴӸ������崫��������� | |
| D�� | ������������ͬʱ����������ܿ��ܼ��� | |
| E�� | Ϊ��������������ܣ�����ͬʱ������������������������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ������0.02 s | B�� | �����ѹ��ЧֵΪ220 V�� | ||
| C�� | t=$\frac{1}{200}$ sʱ��e�����ֵ | D�� | t=0ʱ����Ȧƽ���������洹ֱ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ��������Ϊ������壬�п��ܶԱ���������� | |
| B�� | ����������ֱ���˶�ʱ������������һ������ | |
| C�� | �������������������������������һ������ | |
| D�� | �������������������������������һ������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 �ڹ⻬��ˮƽ���ϣ������������ֵ�ɵ�С��A��B���������֮��ľ�����������������������ijһ����O������Բ���˶�����ͼ��ʾ����֪С��A������ΪmA���������qA��С��B������ΪmB���������qB����mA��mB��qB��qA��A��B����ľ���ΪL������������Ϊk���������ж���ȷ���ǣ�������
�ڹ⻬��ˮƽ���ϣ������������ֵ�ɵ�С��A��B���������֮��ľ�����������������������ijһ����O������Բ���˶�����ͼ��ʾ����֪С��A������ΪmA���������qA��С��B������ΪmB���������qB����mA��mB��qB��qA��A��B����ľ���ΪL������������Ϊk���������ж���ȷ���ǣ�������| A�� | С��A��Բ���˶��İ뾶rA=$\frac{{{q_B}L}}{{{q_A}+{q_B}}}$ | |
| B�� | С��B��Բ���˶��İ뾶rB=$\frac{{{m_A}L}}{{{m_A}+{m_B}}}$ | |
| C�� | С��A��Բ���˶�������TA=2��$\sqrt{\frac{{{m_A}{m_B}{L^3}}}{{k{q_A}{q_B}��{m_A}+{m_B}��}}}$ | |
| D�� | С��B��Բ���˶������ٶ�vB=$\sqrt{\frac{{k{q_A}{q_B}{m_A}}}{{��{m_A}+{m_B}��{m_B}L}}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
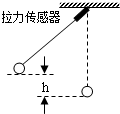 ̽��С�����ô������о�С���ڰڶ������еĻ�е���غ���ɣ�ʵ��װ����ͼ��ʾ�������㴦װ���������������ɼ�¼С���ڰڶ������и�ʱ�̵�����ֵ�������ߵ������Ͱڶ������а��߳��ȵı仯���������ٶ�Ϊg��ʵ��������£�
̽��С�����ô������о�С���ڰڶ������еĻ�е���غ���ɣ�ʵ��װ����ͼ��ʾ�������㴦װ���������������ɼ�¼С���ڰڶ������и�ʱ�̵�����ֵ�������ߵ������Ͱڶ������а��߳��ȵı仯���������ٶ�Ϊg��ʵ��������£��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
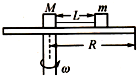 ��ͼ��ʾ��һԲ�̿���������ֱ����ˮƽ����ת����Բ�̰뾶ΪR���ס���������������ֱ�ΪM��m��M��m���������嶼�ɿ����ʵ㣬������Բ��֮������Ħ������Ϊ��ѹ���Ħ̱����������ó�ΪL����������һ��L��R���������������ת��λ���ϣ��ס���֮������������ذ뾶������ֱ���Ӿ�ֹ��ʼ����Բ�̵�ת�٣�Ҫʹ��������Բ�̲�������Ի�����Բ����ת�Ľ��ٶ����ֵ��1�����Ѽס���������һ����Բ�̵ı�Եƽ�ƣ�ʹ��λ��Բ�̵ı�Ե���ס���֮���������Ȼ�ذ뾶������ֱ���ٴδӾ�ֹ��ʼ����Բ�̵�ת�٣�Ҫʹ��������Բ�̲�������Ի�����Բ����ת�Ľ��ٶ����ֵ��2�����1����2��������
��ͼ��ʾ��һԲ�̿���������ֱ����ˮƽ����ת����Բ�̰뾶ΪR���ס���������������ֱ�ΪM��m��M��m���������嶼�ɿ����ʵ㣬������Բ��֮������Ħ������Ϊ��ѹ���Ħ̱����������ó�ΪL����������һ��L��R���������������ת��λ���ϣ��ס���֮������������ذ뾶������ֱ���Ӿ�ֹ��ʼ����Բ�̵�ת�٣�Ҫʹ��������Բ�̲�������Ի�����Բ����ת�Ľ��ٶ����ֵ��1�����Ѽס���������һ����Բ�̵ı�Եƽ�ƣ�ʹ��λ��Բ�̵ı�Ե���ס���֮���������Ȼ�ذ뾶������ֱ���ٴδӾ�ֹ��ʼ����Բ�̵�ת�٣�Ҫʹ��������Բ�̲�������Ի�����Բ����ת�Ľ��ٶ����ֵ��2�����1����2��������| A�� | $\sqrt{\frac{mR+MR-ML}{mL}}$ | B�� | $\sqrt{\frac{R}{L}}$ | C�� | $\sqrt{\frac{2R-L}{L}}$ | D�� | $\sqrt{\frac{M��R-L��}{mR}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com