
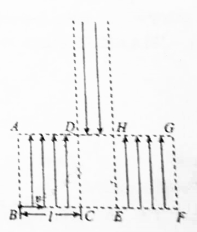
 ��ͼ��ʾ�������߳���Ϊl������������ABCD��EFGH������ֱ���ϵ���ǿ�糡��DH�Ϸ����㹻������ֱ���µ���ǿ�糡��һ����������ӣ�����Ϊm�������Ϊq�����ٶ�v��B����BC����������ǿ�糡����֪���������ڵij�ǿ��С��ȣ���E=$\frac{m{v}^{2}}{ql}$������CDHE�����ڼ��Ϻ��ʵĴ�ֱֽ���������ǿ�ų������Ӿ����ôų���ǡ�ܴ�DH���е���ֱ�������˵糡�����ӵ��������ƣ���
��ͼ��ʾ�������߳���Ϊl������������ABCD��EFGH������ֱ���ϵ���ǿ�糡��DH�Ϸ����㹻������ֱ���µ���ǿ�糡��һ����������ӣ�����Ϊm�������Ϊq�����ٶ�v��B����BC����������ǿ�糡����֪���������ڵij�ǿ��С��ȣ���E=$\frac{m{v}^{2}}{ql}$������CDHE�����ڼ��Ϻ��ʵĴ�ֱֽ���������ǿ�ų������Ӿ����ôų���ǡ�ܴ�DH���е���ֱ�������˵糡�����ӵ��������ƣ������� ��1��������ABCD������ƽ���˶���Ӧ����ƽ���˶��켣��������ų����ȣ�
��2�������ڴų���������Բ���˶������������ṩ����������ţ�ٵڶ����ɿ�������Ÿ�Ӧǿ�ȴ�С��
��3���ֱ���������ڵ糡���ų��е��˶�ʱ�䣬Ȼ����������ܵ��˶�ʱ�䣮
��� �⣺��1��������ABCD��������ƽ���˶���
ˮƽ����l=vt��
���ٶȣ�a=$\frac{qE}{m}$=$\frac{{v}^{2}}{l}$��
��ֱ����d=$\frac{1}{2}$at2=$\frac{1}{2}$$\frac{{v}^{2}}{l}$��$\frac{l}{v}$��2=$\frac{1}{2}$l��
�������ABCD����ʱ�س�ǿ������ٶȣ�vy=at=$\frac{{v}^{2}}{l}$��$\frac{l}{v}$=v�� �ٶ�ƫ��ǣ�tan��=$\frac{{v}_{y}}{v}$=1����=$\frac{��}{4}$��
�ٶ�ƫ��ǣ�tan��=$\frac{{v}_{y}}{v}$=1����=$\frac{��}{4}$��
���Ӵ�$\overline{DH}$�е���ֱ��������糡���ɼ���֪ʶ�ã�
$\overline{OD}$=$\frac{1}{2}$l��${\overline{OD}}^{2}$+$��{\frac{l}{2}��}^{2}$=R2��
��ã�R=$\frac{\sqrt{2}}{2}l$��
R=$\overline{OD}+\frac{1}{2}\overline{DH}$��
��ã�$\overline{DH}$=��$\sqrt{2}$-1��l��
��2����������ų����ٶȴ�С��v��=$\sqrt{2}$v��
�����ڴų���������Բ���˶������������ṩ����������ţ�ٵڶ����ɵã�qv��B=m$\frac{v{��}^{2}}{R}$��
��ã�B=$\frac{2mv}{ql}$��
��3����������糡��ƫת���˶�ʱ�䣺t1=$\frac{l}{v}$��
�����ڴų�������ƫת���˶�ʱ�䣺t2=$\frac{��}{2��}$T=$\frac{\frac{��}{4}}{2��}$��$\frac{2��m}{qB}$=$\frac{��l}{8v}$��
�������Ϸ��糡�м��ٵ��������ʱ�䣺t3=$\frac{\sqrt{2}v}{a}$��
�����˶��켣��ͼ��ʾ�����ݶԳ��Կ�֪�������˶�����ʱ�䣺
t=2��t1+t2+t3��=$\frac{2l}{v}$��1+$\sqrt{2}$+$\frac{��}{8}$����
�𣺣�1�����Ӵų��Ŀ���$\overline{DH}$Ϊ����$\sqrt{2}$-1��l��
��2�����Ӵų��ĴŸ�Ӧǿ���СΪ��$\frac{2mv}{ql}$��
��3�����Ӵ�B�����뵽��EFGH���ǵ糡�����������ʱ��Ϊ��$\frac{2l}{v}$��1+$\sqrt{2}$+$\frac{��}{8}$����
���� ���⿼���������ڵ糡��ų��е��˶��������˶����̸��ӣ�������������˶����̡����������˶��켣�ǽ����ǰ�ᣬ���������˶��켣��Ӧ����ƽ���˶�������ţ�ٵڶ����ɿ��Խ��⣬����ʱע�⼸��֪ʶ��Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
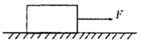 ��ͼ��ʾ���ڴֲڵ�ˮƽ���ϣ��������F���������ɾ�ֹ��ʼ���ȼ���ֱ�� �˶���������3s��ȥ����F�������ˮƽ�������������ֱ���˶����־�9sֹͣ�˶����ڴ˹����У�����ȼ����˶����ȼ����˶���λ��֮���ǣ�������
��ͼ��ʾ���ڴֲڵ�ˮƽ���ϣ��������F���������ɾ�ֹ��ʼ���ȼ���ֱ�� �˶���������3s��ȥ����F�������ˮƽ�������������ֱ���˶����־�9sֹͣ�˶����ڴ˹����У�����ȼ����˶����ȼ����˶���λ��֮���ǣ�������| A�� | 1��3 | B�� | 3��1 | C�� | 1��9 | D�� | 9��1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
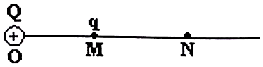 ������е�0���һ����Q=l.0��10 -9C��ֱ��MN��O�㣬OM=30cm��M�����һ����q=-2.0��10 -9C����ͼ��ʾ����
������е�0���һ����Q=l.0��10 -9C��ֱ��MN��O�㣬OM=30cm��M�����һ����q=-2.0��10 -9C����ͼ��ʾ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ����Ϊm������Ϊq���������ٶ�v��A����ֱ��AOB��������ų�����C������ų���OC��OB��60��ǣ�Բ�δų��뾶ΪR�������������������ڴų��еģ�������
����Ϊm������Ϊq���������ٶ�v��A����ֱ��AOB��������ų�����C������ų���OC��OB��60��ǣ�Բ�δų��뾶ΪR�������������������ڴų��еģ�������| A�� | �˶�ʱ��Ϊ$\frac{2��m}{3qB}$ | B�� | �˶�ʱ��Ϊ$\frac{��m}{3qB}$ | ||
| C�� | �˶��뾶Ϊ$\sqrt{3}$R | D�� | �˶��뾶Ϊ$\frac{\sqrt{3}}{3}$R |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
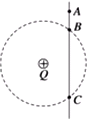 ��ͼ��ʾ���⻬��Եϸ����ֱ���ã������������QΪԲ�ĵ�ijԲ����B��C���㣬����Ϊm���������-q���п�С��Ӹ���A�����ٶ��»�����֪q?Q��AB=h��С��B��ʱ���ٶȴ�СΪ$\sqrt{7gh}$����
��ͼ��ʾ���⻬��Եϸ����ֱ���ã������������QΪԲ�ĵ�ijԲ����B��C���㣬����Ϊm���������-q���п�С��Ӹ���A�����ٶ��»�����֪q?Q��AB=h��С��B��ʱ���ٶȴ�СΪ$\sqrt{7gh}$�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��һ������Ϊ1kg��С����ֱ�����׳�����������׳��㣬�˶�����������������С�㶨���������˶������෴���ù��̵�v-tͼ����ͼ��ʾ��gȡ10m/s2������˵������ȷ���ǣ�������
��һ������Ϊ1kg��С����ֱ�����׳�����������׳��㣬�˶�����������������С�㶨���������˶������෴���ù��̵�v-tͼ����ͼ��ʾ��gȡ10m/s2������˵������ȷ���ǣ�������| A�� | С�����������������������ʱ��֮��Ϊ2��3 | |
| B�� | С������������������С֮��Ϊ5��1 | |
| C�� | С����ص��׳�����ٶȴ�СΪ8$\sqrt{6}$m/s | |
| D�� | С����������У��ܵ����ϵĿ������������ڳ���״̬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ij���ȵij���������ͼ��ʾ��A��B�������ˮƽ�����ϲ��ŷ���һ������ˮƽ��F��ֱ��B�������B���壬ʹA��B�����Ա��־�����F���������˶���������
��ij���ȵij���������ͼ��ʾ��A��B�������ˮƽ�����ϲ��ŷ���һ������ˮƽ��F��ֱ��B�������B���壬ʹA��B�����Ա��־�����F���������˶���������| A�� | ����A��ˮƽ�������������������ã��Һ���Ϊ�� | |
| B�� | ����A��ˮƽ�������������������ã��Һ���Ϊ�� | |
| C�� | B��A��ѹ�����������A��Ħ���� | |
| D�� | B��A��������������F������ͬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ����ʾ��һ���ʵ��ɵ��¶˹̶���ˮƽ���ϣ��϶˷���һ���壨�����뵯�ɲ����ӣ�����ʼʱ���崦�ھ�ֹ״̬��������ֱ���ϵ�����F�����������ϣ�ʹ���忪ʼ�������ȼ����˶�������F������λ��x�Ĺ�ϵ��ͼb��ʾ��g=10m/s2��������ȷ�Ľ����ǣ�������
��ͼ����ʾ��һ���ʵ��ɵ��¶˹̶���ˮƽ���ϣ��϶˷���һ���壨�����뵯�ɲ����ӣ�����ʼʱ���崦�ھ�ֹ״̬��������ֱ���ϵ�����F�����������ϣ�ʹ���忪ʼ�������ȼ����˶�������F������λ��x�Ĺ�ϵ��ͼb��ʾ��g=10m/s2��������ȷ�Ľ����ǣ�������| A�� | �����뵯�ɷ���ʱ�����ɴ���ѹ��״̬ | |
| B�� | ���ɵľ���ϵ��Ϊ7.5N/cm | |
| C�� | ���������Ϊ20kg | |
| D�� | ����ļ��ٶȴ�СΪ5m/s2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
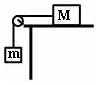 ��ͼ��ʾ����֪M��m�����ƻ��ּ����ӵ�����������M��mǡ���������˶�������M��m ������M��m������Ķ�Ħ������ͬ��������
��ͼ��ʾ����֪M��m�����ƻ��ּ����ӵ�����������M��mǡ���������˶�������M��m ������M��m������Ķ�Ħ������ͬ��������| A�� | ����M��m���������˶� | |
| B�� | ����M��m�������˶������ٶ�a=$\frac{��M+m��g}{M}$ | |
| C�� | ����M��m�������˶������ٶ�a=$\frac{��M-m��g}{M}$ | |
| D�� | �������������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com