
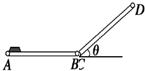
 如图所示为仓库中常用的皮带传输装置示意图,它由两台皮带传送这机组成,一台水平传送,A、B两端相距3m,另一台倾斜,其传送带与地面的倾角θ=37°,C、D两端相距4.45m,B、C相距很近.水平部分AB以v0=5m/s的速率顺时针转动.将一袋质量为10kg的大米无初速度放在A端,到达B端后,米袋继续沿倾斜的CD部分运动,不计米袋在BC处的能量损失.已知米袋与传送带间的动摩擦因数均为0.5,求:
如图所示为仓库中常用的皮带传输装置示意图,它由两台皮带传送这机组成,一台水平传送,A、B两端相距3m,另一台倾斜,其传送带与地面的倾角θ=37°,C、D两端相距4.45m,B、C相距很近.水平部分AB以v0=5m/s的速率顺时针转动.将一袋质量为10kg的大米无初速度放在A端,到达B端后,米袋继续沿倾斜的CD部分运动,不计米袋在BC处的能量损失.已知米袋与传送带间的动摩擦因数均为0.5,求:分析 (1)米袋放上传送带先做匀加速直线运动,求出米袋达到传送带速度所需的时间和位移,即可判断到达B点的速度
(2)由牛顿第二定律可求得米的加速度,因米袋的最大速度只能为5m/s,则应判断米袋到达B点时是否已达最大速度,若没达到,则由位移与速度的关系可求得B点速度,若达到,则以5m/s的速度冲上CD;在CD面上由牛顿第二定律可求得米袋的加速度,则由位移和速度的关系可求得上升的最大距离,即可判断是否到达D点;
(3)米袋在CD上应做减速运动,若CD的速度较小,则米袋的先减速到速度等于CD的速度,然后可能减小到零,求得最小速度
解答 解:(1)米袋在传送带AB上,与之有相对滑动时μmg=ma1
a1=μg=0.5×10m/s2=5m/s2
达到共同速度所需时间为
v=a1t1
t1=$\frac{{v}_{0}}{{a}_{1}}=\frac{5}{5}s=1s$
在1s内通过的位移为${x}_{1}=\frac{{v}_{0}}{2}{t}_{1}=\frac{5}{2}×1m=2.5m$<3m,到达B点的速度为vB=v0=5m/s
(2)设米袋在CD上运动的加速度大小为a,由牛顿第二定律得mgsinθ+μmgcosθ=ma
代入数据得 a2=10 m/s2
所以能滑上的最大距离 s=$\frac{{v}_{0}^{2}}{2{a}_{2}}=\frac{{5}^{2}}{2×10}m=1.25m$<4.45m
不能到达D点
(3)设CD部分运转速度为v1时米袋恰能到达D点(即米袋到达D点时速度恰好为零),则米
袋速度减为v1之前的加速度为a3=-g(sinθ+μcosθ)=-10 m/s2
米袋速度小于v1至减为零前的加速度为a4=-g(sinθ-μcosθ)=-2 m/s2
由$\frac{{v}_{1}^{2}{-v}_{0}^{2}}{2{a}_{3}}+\frac{0{-v}_{1}^{2}}{2{a}_{4}}=4.45$
代入数据,解得 v1=4m/s,
答:(1)米袋到达B点的速度为5m/s;
(2)若CD部分传送带不运转,米袋不能运动到D端;
(3)若要米袋能被送到D端,CD部分顺时针运转的最小速为4m/s
点评 本题是个多过程问题,关键要理清各个阶段的运动情况,结合牛顿运动定律和运动学进行求解


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中物理 来源: 题型:实验题
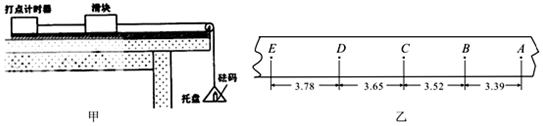
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 地面 | B. | 坐在他身边的乘客 | ||
| C. | 铁路边的树木 | D. | 窗外的山峰 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,重力为300N的物体在细绳AC和BC的作用下处于静止状态,细绳AC和BC于竖直方向的夹角分别为30°和60°,求AC绳的弹力FA和BC绳的弹力FB的大小.
如图所示,重力为300N的物体在细绳AC和BC的作用下处于静止状态,细绳AC和BC于竖直方向的夹角分别为30°和60°,求AC绳的弹力FA和BC绳的弹力FB的大小.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
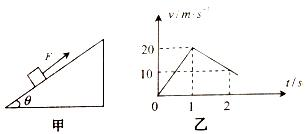 如图甲所示,质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上,t=0时刻 对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的v-t图象如图乙所示.g=10m/s2,试求:
如图甲所示,质量为m=1kg的物体置于倾角为θ=37°的固定且足够长的斜面上,t=0时刻 对物体施以平行于斜面向上的拉力F,t1=1s时撤去拉力,物体运动的v-t图象如图乙所示.g=10m/s2,试求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
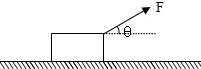 如图所示,质量为m=2kg的物体与水平地面的动摩擦因素为μ=0.2,现对物体施加一大小为10N,方向与水平方向成θ=37°角斜向上的力F,使之向右做匀加速直线运动,求:
如图所示,质量为m=2kg的物体与水平地面的动摩擦因素为μ=0.2,现对物体施加一大小为10N,方向与水平方向成θ=37°角斜向上的力F,使之向右做匀加速直线运动,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
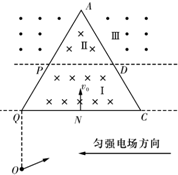 为了使粒子经过一系列的运动后,又以原来的速率沿相反方向回到原位,可设计如下的一个电磁场区域(如图所示):水平线QC以下是水平向左的匀强电场,区域Ⅰ(梯形PQCD)内有垂直纸面向里的匀强磁场,磁感应强度为B;区域Ⅱ(三角形APD)内的磁场方向与Ⅰ内相同,区域Ⅲ(虚线PD之上、三角形APD以外)的磁场与Ⅱ内大小相等、方向相反.已知等边三角形AQC的边长为2L,P、D分别为AQ、AC的中点.带正电的粒子从Q点正下方、距离Q点为L的O点以某一速度射出,在电场力作用下从QC边中点N以速度v0垂直QC射入区域Ⅰ,再从P点垂直AQ射入区域Ⅲ,又经历一系列运动后返回O点.(粒子重力忽略不计)求:
为了使粒子经过一系列的运动后,又以原来的速率沿相反方向回到原位,可设计如下的一个电磁场区域(如图所示):水平线QC以下是水平向左的匀强电场,区域Ⅰ(梯形PQCD)内有垂直纸面向里的匀强磁场,磁感应强度为B;区域Ⅱ(三角形APD)内的磁场方向与Ⅰ内相同,区域Ⅲ(虚线PD之上、三角形APD以外)的磁场与Ⅱ内大小相等、方向相反.已知等边三角形AQC的边长为2L,P、D分别为AQ、AC的中点.带正电的粒子从Q点正下方、距离Q点为L的O点以某一速度射出,在电场力作用下从QC边中点N以速度v0垂直QC射入区域Ⅰ,再从P点垂直AQ射入区域Ⅲ,又经历一系列运动后返回O点.(粒子重力忽略不计)求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com