

���� ��1�����ݸ����ĵ�Դ������������ֵ��ȷ�����������Ľӷ���ͬʱ����ʵ��İ�ȫ�Ժ�ȷ��Ҫ����ȷ�DZ���ѡ��
��2�����ݵ����ʾ���仯����ȷ�����Ӱ�죬���ѡ������С�Ľӷ���
��� �⣺��1����������Ϊ10�����ʻ���������ֻ�ܲ�������Ļ�������������ֻ��ѡ��R1������ֵС�ڴ�����裬Ϊ�˱��ڲ�������ȫ��Ӧѡ���ѹ�ӷ���
��Դ�綯��Ϊ5V��Ϊ�����ʵ�龫�ȣ���ѹ��Ӧѡ��3V���̣���ѡ��V2�����·�е������ԼΪ$\frac{3}{10}$=0.3A���ʵ�����ѡ��A2��
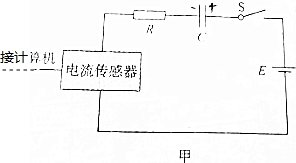
��2�������������仯��Խϴ�ѹ�������仯��Խ�С��˵����ѹ���ķ����ϴ�Ӧ���õ������ڽӷ�����ѡͼ�ң�
�ʴ�Ϊ����1��R1����ѹ��A2��V2��
��2��ͼ��
���� ���⿼�������������е�ʵ���DZ�ѡ���Լ��ӷ���ѡ��Ҫע����ȷ������������Сʱ��Ӧ���÷�ѹ�ӷ���


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ��һ��$\frac{3}{4}$Բ���ι⻬Բ�ܹ��ABC����������ֱƽ���ڣ�����뾶ΪR����A ����ˮƽ����AD��ӣ�������Բ��O�ȸߣ�MN �Ƿ���ˮƽ�����ϳ�Ϊ3R����Ȳ��Ƶļ���棬���M����λ��A�㣮һ������Ϊm��С���A���ܿ����Ϸ�ij���ɾ�ֹ�ͷţ��������ǿ���������С��ɿ����ʵ㣬�������ٶ�Ϊg����ô����˵������ȷ���ǣ�������
��ͼ��ʾ��һ��$\frac{3}{4}$Բ���ι⻬Բ�ܹ��ABC����������ֱƽ���ڣ�����뾶ΪR����A ����ˮƽ����AD��ӣ�������Բ��O�ȸߣ�MN �Ƿ���ˮƽ�����ϳ�Ϊ3R����Ȳ��Ƶļ���棬���M����λ��A�㣮һ������Ϊm��С���A���ܿ����Ϸ�ij���ɾ�ֹ�ͷţ��������ǿ���������С��ɿ����ʵ㣬�������ٶ�Ϊg����ô����˵������ȷ���ǣ�������| A�� | Ҫʹ���ܴ�C��������ܴ����ϣ�����C��ʱ���ٶ�����Ϊ$\sqrt{gR}$ | |
| B�� | Ҫʹ���ܴ�C��������ܴ����ϣ�����C��ʱ���ٶ�����Ϊ$\sqrt{\frac{gR}{2}}$ | |
| C�� | �����C�������ǡ���ܴ��ӵ�M�ˣ�����C��ʱ�Թܵ���������СΪ$\frac{mg}{2}$ | |
| D�� | Ҫʹ����ͨ��C���䵽�����ϣ�����A������߶���5R |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��һ��ĩ���ٶ� | B�� | �ڶ���ĩ�ٶ� | ||
| C�� | ���һ���ڵ�λ�� | D�� | ���һ���ڵ�λ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ·��Ϊ50m | B�� | λ�ƴ�СΪ40m���������� | ||
| C�� | �ٶȸı����Ĵ�СΪ40m/s | D�� | ƽ���ٶȴ�СΪ20m/s���������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ����ij����ĵ糡�߷ֲ���A��B�ǵ糡�е����㣬A��B����ĵ糡ǿ�ȷֱ���EA��EB�����Ʒֱ��Ǧ�A�ͦ�B�������ǵĴ�С��ϵ��ȷ���ǣ�������
��ͼ��ʾ����ij����ĵ糡�߷ֲ���A��B�ǵ糡�е����㣬A��B����ĵ糡ǿ�ȷֱ���EA��EB�����Ʒֱ��Ǧ�A�ͦ�B�������ǵĴ�С��ϵ��ȷ���ǣ�������| A�� | EA��EB | B�� | EA��EB | C�� | ��A����B | D�� | ��A����B |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �㼣��¼�������˶���ʱ�� | |
| B�� | �㼣��¼�������ڲ�ͬʱ�̵�λ�ú�ij��ʱ���ڵ�λ�� | |
| C�� | ʵ�������бز����ٵ������ | |
| D�� | ʵ�������бز����ٵ��ǿ̶ȳ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 �ھ�����ϰ�У�ij�ս����ӷɻ������£������ٶ�ͼ����ͼ��ʾ�����й��ڸÿս�����0��t1��t1��t2ʱ���ڵ�ƽ���ٶ�$\overline{v}$�Ľ�����ȷ���ǣ�������
�ھ�����ϰ�У�ij�ս����ӷɻ������£������ٶ�ͼ����ͼ��ʾ�����й��ڸÿս�����0��t1��t1��t2ʱ���ڵ�ƽ���ٶ�$\overline{v}$�Ľ�����ȷ���ǣ�������| A�� | 0��t1�ڣ�$\overline{v}$=$\frac{{v}_{1}}{2}$ | B�� | t1��t2�ڣ�$\overline{v}$��$\frac{{v}_{1}+{v}_{2}}{2}$ | ||
| C�� | t1��t2�ڣ�$\overline{v}$=$\frac{{v}_{1}+{v}_{2}}{2}$ | D�� | t1��t2�ڣ�$\overline{v}$��$\frac{{v}_{1}+{v}_{2}}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com