
 ��ͼ��ʾ����ֱƽ��MN��ֽ�洹ֱ��MN�Ҳ�Ŀռ�����Ŵ�ֱֽ�����ڵ���ǿ�ų���ˮƽ�������ǿ�糡��MN����ˮƽ��⻬���Ҳ��ˮƽ��ֲڣ�����Ϊm������A��ֹ��MN����ˮƽ���ϣ���֪����������磬������Ĵ�СΪΪq��һ����Ϊ$\frac{1}{3}m$�IJ����������B���ٶ�v0��������A������������ײ����ײǰ������A�ĵ�������ֲ��䣮��
��ͼ��ʾ����ֱƽ��MN��ֽ�洹ֱ��MN�Ҳ�Ŀռ�����Ŵ�ֱֽ�����ڵ���ǿ�ų���ˮƽ�������ǿ�糡��MN����ˮƽ��⻬���Ҳ��ˮƽ��ֲڣ�����Ϊm������A��ֹ��MN����ˮƽ���ϣ���֪����������磬������Ĵ�СΪΪq��һ����Ϊ$\frac{1}{3}m$�IJ����������B���ٶ�v0��������A������������ײ����ײǰ������A�ĵ�������ֲ��䣮������ ��1������A��B�ǵ�����ײ��ϵͳ�����غ㡢��е��Ҳ�غ㣬���ݶ����غ㶨�ɺͻ�е���غ㶨����ʽ���������õ���ײ������A���ٶȴ�СvA��
��2������A�����ų�����������ҵĵ糡�������µ�����������������֧����������Ļ���Ħ�������DZ�����˶�����Ħ������糡��ƽ��ʱ�ٶ������ƽ��������ʽ�������ٶȣ����ݶ��ܶ�����ʽ���˹���������A�˷�Ħ���������Ĺ�W�����ݶ���������ʽ���˹�����������ʱ��t��
��� �⣺��1����A��B��ײ����ٶȷֱ�ΪvA��vB������A��B����������ײ�����������ܾ��غ㣬���У�$\frac{1}{3}m{v_0}=\frac{1}{3}m{v_B}+m{v_A}$ ��
$\frac{1}{2}•\frac{1}{3}mv_0^2=\frac{1}{2}•\frac{1}{3}m{v_B}^2+\frac{1}{2}mv_A^2$ ��
�����٢ڿɵã�
${v_A}=\frac{1}{2}{v_0}$ ��
��2��a��A���ٶȴﵽ���ֵvmʱ����Ϊ�㣬������ͼ��ʾ��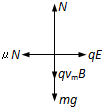
��ֱ�������Ϊ�㣬�У�N=qvmB+mg ��
ˮƽ�������Ϊ�㣬�У�qE=��N ��
���ݶ��ܶ������У�$qEl-W=\frac{1}{2}mv_m^2-\frac{1}{2}mv_A^2$ ��
�����ۢܢݢ�������������ݿɵã�$W=4��mgl-\frac{3}{8}mv_0^2$
b������һ��
�ڴ˹����У���A�����˶���ƽ���ٶ�Ϊ$\bar v$�����ݶ��������У�
$qEt-��\bar Nt=m{v_m}-m{v_A}$ ��
$\overline{N}=mg+q\bar vB$ ��
��������$\bar vt=l$ ��
�����ۢܢݢߢ�Ტ����������ݿɵã�
$t=\frac{l}{v_0}+\frac{v_0}{6��g}$
��������
������ʱ��A�����˶����ٶ�Ϊv��ȡһ�κ���ʱ�̵ļ���ʱ���t����˶�ʱ�����ٶȵĸı���Ϊ��v�����ݶ��������У�$\sum qE��t-\sum �̣�mg+qvB����t=\sum m��v$��
��$\sum v��t=l$ ��
$\sum m��v=m{v_m}-m{v_A}$ ��
�����ۢܢݢߢ�Ტ����������ݿɵã�
$t=\sum��t=\frac{l}{v_0}+\frac{v_0}{6��g}$
�𣺣�1����ײ������A���ٶȴ�СvAΪ$\frac{{v}_{0}}{2}$��
��2��a���˹���������A�˷�Ħ���������Ĺ�WΪ$4��mgl-\frac{3}{8}m{v}_{0}^{2}$��
b���˹�����������ʱ��tΪ$\frac{l}{{v}_{0}}+\frac{{v}_{0}}{6��g}$��
���� ����ؼ�����ȷ����������ײ������ϵͳ�����غ㡢��е��Ҳ�غ㣻����A�����˶��������DZ�����˶�����Ħ�������ӵ����ڵ糡��ʱ���ٶȴﵽ���ֵ����϶��ܶ����Ͷ���������ʽ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ţ�ٵ�һ�����ֽй��Զ��ɣ�����ֻ�����˶��������ϲŻ���ֳ��� | |
| B�� | �ں�����Ϊ��������£������Ƶ���ţ�ٵ�һ���� | |
| C�� | �������������˶�״̬�ı��ԭ���ٶ��Ǻ����������������ϵ��������� | |
| D�� | �������뷴������ͬʱ������ͬʱ��ʧ������Ч������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����ǵ�����ת���ڵ�$\frac{1}{{{{60}^2}}}$�� | |
| B�� | ���ļ��ٶ�������������ٶȵ�$\frac{1}{{{{60}^2}}}$�� | |
| C�� | ���ٶ��ǵ�����ת�ر����ٶȵ�602�� | |
| D�� | ���ٶ��ǵ�����ת�ر����ٶȵ�602�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
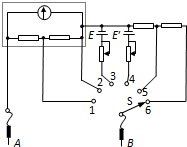 ��ͼ��ʾ����һ�������̶��õ���ļ�·ͼ��������Ͳ��ѹʱ�����������̣�����������λ��������裮����˵����ȷ���ǣ�������
��ͼ��ʾ����һ�������̶��õ���ļ�·ͼ��������Ͳ��ѹʱ�����������̣�����������λ��������裮����˵����ȷ���ǣ�������| A�� | ������S����1��2����λ����ʱ�����õ���������ǵ������ҵ���1λ����ʱ�����̱�2λ�õĴ� | |
| B�� | ������S����3��4����λ����ʱ�����õ���������ǵ��裬��AΪ�ڱ��� | |
| C�� | ������S����5��6����λ����ʱ�����õ���������ǵ�ѹ���ҵ���5λ����ʱ�����̱�6λ�õĴ� | |
| D�� | ������S��������λ����ʱ������Ҫ��A��B�����ʶ̽ӣ��Ե�����е��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
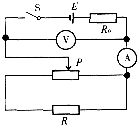 ��ͼ��ʾΪһֱ����·����Դ����С��R0�������������������ֵС��R���ڻ����������Ļ�ƬP�����Ҷ˻�������˵Ĺ����У�����˵��������ǣ�������
��ͼ��ʾΪһֱ����·����Դ����С��R0�������������������ֵС��R���ڻ����������Ļ�ƬP�����Ҷ˻�������˵Ĺ����У�����˵��������ǣ�������| A�� | ��ѹ����ʾ��һֱ���� | B�� | ��������ʾ��һֱ���� | ||
| C�� | ����R0���ĵĹ���һֱ���� | D�� | ��Դ����������ȼ�С������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
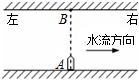
| A�� | С���ܵ���������B�� | |
| B�� | С���������λ����ˮ���ٶ��� | |
| C�� | С���������ʱ����ˮ���ٶ��� | |
| D�� | С���������λ����ˮ���ٶ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ�ĵ�·�У���Դ�綯��ΪE���ڵ���Ϊr��LΪС���ݣ����˿���������Ϊ���䣩��R1��R2Ϊ��ֵ���裬R3Ϊ�������裬����ֵ�Ĵ�С�������ǿ�ȵ���ǿ����С���պϿ���S�������ǿ�ȼ�����������
��ͼ��ʾ�ĵ�·�У���Դ�綯��ΪE���ڵ���Ϊr��LΪС���ݣ����˿���������Ϊ���䣩��R1��R2Ϊ��ֵ���裬R3Ϊ�������裬����ֵ�Ĵ�С�������ǿ�ȵ���ǿ����С���պϿ���S�������ǿ�ȼ�����������| A�� | ��·��·�˵�ѹ����С | B�� | ����L���䰵 | ||
| C�� | R2���˵ĵ�ѹ����С | D�� | ����������ĵ������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
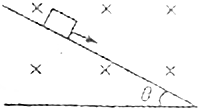 ��ͼ��ʾ��һ�⻬����Եб�棬��Ǧ�=37�㣬һ����m=0.02kg�����壨����Ϊ�ʵ㣩��б���ϵ�ij���ɾ�ֹ��ʼ�»����������Ĵ�����q=+10-2C����ֱֽ���������ǿ�ų�B=4.0T������������б�����˶���������ʼ���б���»��������루gȡ10m/s2��sin37��=0.6��cos37��=0.8��б���㹻������
��ͼ��ʾ��һ�⻬����Եб�棬��Ǧ�=37�㣬һ����m=0.02kg�����壨����Ϊ�ʵ㣩��б���ϵ�ij���ɾ�ֹ��ʼ�»����������Ĵ�����q=+10-2C����ֱֽ���������ǿ�ų�B=4.0T������������б�����˶���������ʼ���б���»��������루gȡ10m/s2��sin37��=0.6��cos37��=0.8��б���㹻�������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com