
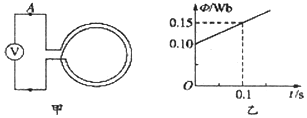
���� ��1����ͼ�����ͨ���ı仯�ʣ����ݷ����ڵ�Ÿ�Ӧ���������·�и�Ӧ�綯�ƣ�
��2���������⣬��Ȧ���д�ֱֽ���������ǿ�ų������Դ�����Ȧ�ڵĴŸ��߷���Ϊ������
��3��������ζ����жϵ綯�Ƶķ���ȷ����ѹ���Ľ������ӷ���
��� �⣺��1�����ݷ����ڵ�Ÿ�Ӧ����$E=n\frac{����}{��t}$����
$E=n\frac{����}{��t}=100��\frac{0.15-0.10}{0.1}=50V$
��2���������⣬��Ȧ���д�ֱֽ���������ǿ�ų������Դ�����Ȧ�ڵĴŸ��߷���Ϊ������
��3������ζ����ж�����Ӧ��������Ϊ��ʱ�뷽����Ȧ��Ч�ڵ�Դ������Դ�е����ɵ͵�������ߵ��ƣ���A�˵ĵ��Ƹ���B�˵��ƣ���B�˸ߣ���A��Ӧ�����ѹ���ġ�+���Ľ��������ӣ�
�ʴ�Ϊ����1��50 ��2������3��A��
���� ���⿼����ݷ����ڵ�Ÿ�Ӧ�������Ӧ�綯�ƣ�����ζ����жϸ�Ӧ�綯�Ƶķ����dz����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{t}_{2}}{2{t}_{1}+\sqrt{3}{t}_{2}}$ | B�� | $\frac{2{t}_{1}-\sqrt{3}{t}_{2}}{{t}_{1}}$ | C�� | $\frac{{t}_{2}}{2{t}_{1}-\sqrt{3}{t}_{2}}$ | D�� | $\frac{2{t}_{1}-\sqrt{3}{t}_{2}}{2{t}_{1}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ������m=6kg����龲ֹ��ˮƽ�����ϣ��ܵ���ˮƽ����ɦ�=37��ǵ�������F������֪sin37��=0.6��cos37��=0.8��tan37��=0.75��g=10m/s2��
��ͼ��ʾ������m=6kg����龲ֹ��ˮƽ�����ϣ��ܵ���ˮƽ����ɦ�=37��ǵ�������F������֪sin37��=0.6��cos37��=0.8��tan37��=0.75��g=10m/s2���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | I1��I2=n1��n2 | B�� | U1��U2=n1��n2 | C�� | P1��P2=n1��n2 | D�� | P1=P2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ������·�Ĵ�ͨ���仯Խ�����ĸ�Ӧ�綯��Խ�� | |
| B�� | ijһʱ�̴�����·�Ĵ�ͨ��Ϊ�㣬��·�и�Ӧ�綯��һ��Ϊ�� | |
| C�� | �����·���պϣ���ʹ������·��ͨ�������仯����Ӧ�綯��Ҳһ��Ϊ�� | |
| D�� | ������·�Ĵ�ͨ���仯Խ�죬��Ӧ�綯��Խ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ��1 min�ڣ������ϲ�����������6600J | |
| B�� | ����ݴ����ĵ�������ʾ��Ϊ0.5A | |
| C�� | ����ݲ����ĵ�ѹ����ʾ��Ϊ311V | |
| D�� | ͨ�����ݵĵ����ı���ʽΪi=0.5sin 314t��A�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 0m/s��5m/s | B�� | 4.8m/s��5m/s | C�� | 0m/s��4.8m/s | D�� | 4.8m/s��10m/s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
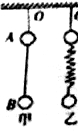 ��ͼ��ʾ������������ͬ��С��A��B����ͼ��������ò����쳤��ϸ�����ӣ�Ȼ����ϸ����������������������OA��˲�䣮A���B��ļ��ٶȷֱ��Ƕ��٣�
��ͼ��ʾ������������ͬ��С��A��B����ͼ��������ò����쳤��ϸ�����ӣ�Ȼ����ϸ����������������������OA��˲�䣮A���B��ļ��ٶȷֱ��Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{v}=\sqrt{\frac{��}{{2��p-{p_0}��}}}$ | B�� | $\frac{1}{v}=\sqrt{\frac{2��}{{��p+{p_0}��}}}$ | C�� | $\frac{1}{v}=\sqrt{\frac{{2��p-{p_0}��}}{2��}}$ | D�� | $\frac{1}{v}=\sqrt{2�ѣ�p-{p_0}��}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com