
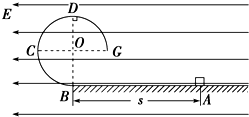
 ��ͼ��ʾ��BCDG�ǹ⻬��Ե��$\frac{3}{4}$Բ�ι����λ����ֱƽ���ڣ�����뾶ΪR���¶���ˮƽ��Ե�����B��ƽ�����ӣ������������ˮƽ�������ǿ�糡�У�����һ����Ϊm���������С���飨����Ϊ�ʵ㣩����ˮƽ����ϣ������ܵ��ĵ糡����СΪ$\frac{3}{4}$mg��������ˮƽ�����Ķ�Ħ������Ϊ0.5���������ٶ�Ϊg��
��ͼ��ʾ��BCDG�ǹ⻬��Ե��$\frac{3}{4}$Բ�ι����λ����ֱƽ���ڣ�����뾶ΪR���¶���ˮƽ��Ե�����B��ƽ�����ӣ������������ˮƽ�������ǿ�糡�У�����һ����Ϊm���������С���飨����Ϊ�ʵ㣩����ˮƽ����ϣ������ܵ��ĵ糡����СΪ$\frac{3}{4}$mg��������ˮƽ�����Ķ�Ħ������Ϊ0.5���������ٶ�Ϊg������ ��1���ɶ��ܶ������������ٶȣ�
��2����ţ�ٵڶ�������������ܵ�����������
��3������Ի����������Ϊ��ʱ���ٶ���С����ţ�ٵڶ����ɿ��������С�ٶȣ�
��� �⣺��1���軬�鵽��B��ʱ���ٶ�Ϊv���ɶ��ܶ����У�
$qES-��mgS=\frac{1}{2}m{v}^{2}$
����$qE=\frac{3mg}{4}$
������ã�$v=\sqrt{\frac{3gR}{2}}$
��2���軬�鵽��C����ٶ�ΪvC��
$qER-mgR=\frac{1}{2}{mv}_{C}^{2}-\frac{1}{2}m{v}^{2}$
��ã�${v}_{C}=\sqrt{gR}$
ˮƽ����ĺ����ṩ������Ϊ��
$F-qE=\frac{{mv}_{C}^{2}}{R}$
��ã�$F=\frac{7}{4}mg$
��3��Ҫʹ����ǡ��ʼ���ع�����У�����Բ���DG��ij�㣬�ɵ糡���������ĺ����ṩ����������ʱ�ٶ���С
����$\sqrt{��qE��^{2}+��mg��^{2}}=\frac{{mv}_{min}^{2}}{R}$
��ã�${v}_{min}=\frac{\sqrt{5gR}}{2}$
�𣺣�1���������ˮƽ����Ͼ���B��s=3R��A���ɾ�ֹ�ͷţ����鵽��B��ʱ�ٶ�Ϊ$\sqrt{\frac{3gR}{2}}$
��2���ڣ�1��������£����鵽��C��ʱ�ܵ��������������С$\frac{7}{4}mg$��
��3���ı�s�Ĵ�С��ʹ����ǡ��ʼ���ع�����У��Ҵ�G��ɳ������������Բ����ϻ��й����е���С�ٶȴ�С$\frac{\sqrt{5gR}}{2}$
���� ���⿼�������ٶȡ����������ٶȷ�Χ�����⣬�������������˶���������ȷ�����ǰ�ᣬӦ�ö��ܶ�����ţ�ٵڶ����ɼ�����ȷ���⣬����ʱҪע�⻬����Բ���˶����ٽ�������


 �������¿��ÿ�ʱ��ҵϵ�д�
�������¿��ÿ�ʱ��ҵϵ�д� Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
Ӣ�żƻ�ͬ����ʱ��Чѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ������洦���������ٶ�g��Ϊ $\frac{G_2}{G_1}g$ | |
| B�� | �������������������֮��Ϊ$\frac{{{G_1}R_2^2}}{{{G_2}R_1^2}}$ | |
| C�� | �����ھ������������������Բ���˶�������T��Ϊ2��$\sqrt{\frac{{{R_2}{G_1}}}{{g{G_2}}}}$ | |
| D�� | ����ĵ�һ�����ٶ������ĵ�һ�����ٶ�֮��Ϊ$\sqrt{\frac{{{G_1}{R_2}}}{{{G_2}{R_1}}}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | $\frac{n_2}{n_2}��\frac{n_3}{n_4}$ | |
| B�� | $\frac{n_2}{n_2}��\frac{n_3}{n_4}$ | |
| C�� | $\frac{n_2}{n_1}$Խ���������ʧ�ĵ繦��Խ�� | |
| D�� | $\frac{n_2}{n_1}$Խ����ѹ��ѹ�����������Խ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ң��������������һ���涨��Ŀ����Խ��������������Ҫ�����������A�ɾ�ֹ��������ˮƽֱ�߹���˶�����B��ɳ���Խ�������������䵽ƽ��EF�Σ���ͼ��ʾ��������ͨ����Զ����P=1.5W��������AB���˶������У��ܵ�������ΪF1=0.3N���ڿ����˶��Ĺ��̲��ƿ�����������֪��������m=0.1kg��AB�ij���L=10.00m��BE�ĸ߶Ȳ�h=1.25m��BE��ˮƽ����s=1.50m�����������ٶ�g=10m/s2����
ң��������������һ���涨��Ŀ����Խ��������������Ҫ�����������A�ɾ�ֹ��������ˮƽֱ�߹���˶�����B��ɳ���Խ�������������䵽ƽ��EF�Σ���ͼ��ʾ��������ͨ����Զ����P=1.5W��������AB���˶������У��ܵ�������ΪF1=0.3N���ڿ����˶��Ĺ��̲��ƿ�����������֪��������m=0.1kg��AB�ij���L=10.00m��BE�ĸ߶Ȳ�h=1.25m��BE��ˮƽ����s=1.50m�����������ٶ�g=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 35km/h | B�� | 45km/h | C�� | 40km/h | D�� | 50km/h |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ��һ����L=0.20m�ġ�U���;�Ե������ˮƽ���30����ǹ̶����ã��ڵ��������ڴ�����ֱ���µ���ǿ�ų����Ÿ�Ӧǿ��B=1.0T��һ������Ϊ0.10Kg�Ľ�������ֱ�����ڵ����ϣ�����ͨ��I=5.0A�ĵ�������������ֹ���������ٶ�g=10m/s2��������
��ͼ��ʾ��һ����L=0.20m�ġ�U���;�Ե������ˮƽ���30����ǹ̶����ã��ڵ��������ڴ�����ֱ���µ���ǿ�ų����Ÿ�Ӧǿ��B=1.0T��һ������Ϊ0.10Kg�Ľ�������ֱ�����ڵ����ϣ�����ͨ��I=5.0A�ĵ�������������ֹ���������ٶ�g=10m/s2��������| A�� | ����Խ�������֧������СΪ$\frac{{\sqrt{3}}}{2}$N | |
| B�� | ����Խ�������֧������СΪ$\frac{{\sqrt{3}-1}}{2}$N | |
| C�� | ����Խ�������Ħ������СΪ$\frac{{\sqrt{3}-1}}{2}$N������ƽ�е������� | |
| D�� | ����Խ�������Ħ������СΪ$\frac{{\sqrt{3}+1}}{2}$N������ƽ�е������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | ��OA���ܵ����������� | B�� | ��OA���ܵ�������С | ||
| C�� | ��OA���ܵ������ȼ�С������ | D�� | ��OA���ܵ�������������С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
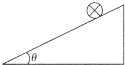 ��ͼ��ʾ�����Ϊ�ȵĹ⻬б��̶���ˮƽ���ϣ�б���ϴ�ֱֽ�����һ����ΪL������Ϊm��ֱ���������������еĵ���I��ֱֽ������ʱ����ʹ�������ֹ��б���ϣ��ɼ�һ��ƽ����ֽ�����ǿ�ų����������ٶ�Ϊg�������йشų�����������ȷ���ǣ�������
��ͼ��ʾ�����Ϊ�ȵĹ⻬б��̶���ˮƽ���ϣ�б���ϴ�ֱֽ�����һ����ΪL������Ϊm��ֱ���������������еĵ���I��ֱֽ������ʱ����ʹ�������ֹ��б���ϣ��ɼ�һ��ƽ����ֽ�����ǿ�ų����������ٶ�Ϊg�������йشų�����������ȷ���ǣ�������| A�� | ���ų�������ֱ���ϣ���B=$\frac{mgtan��}{IL}$ | |
| B�� | ���ų�����ƽ��б�����ϣ���B=$\frac{mgsin��}{IL}$ | |
| C�� | ���ų�����ֱб�����ϣ���B=$\frac{mgsin��}{IL}$ | |
| D�� | ���ų�����ֱб�����ϣ���B=$\frac{mgcos��}{IL}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com