Question

在真空中建立一坐标系，以水平向右为轴正方向，竖直向下为轴正方向，轴垂直纸面向里（图复17-5）．在的区域内有匀强磁场，，磁场的磁感强度的方向沿轴的正方向，其大小．今把一荷质比的带正电质点在，，处静止释放，将带电质点过原点的时刻定为时刻，求带电质点在磁场中任一时刻的位置坐标．并求它刚离开磁场时的位置和速度．取重力加速度。

Answer 1

解法一：

带电质点静止释放时，受重力作用做自由落体运动，当它到达坐标原点时，速度为                              （1）

方向竖直向下．带电质点进入磁场后，除受重力作用外，还受到洛伦兹力作用，质点速度的大小和方向都将变化，洛伦兹力的大小和方向亦随之变化．我们可以设想，在带电质点到达原点时，给质点附加上沿轴正方向和负方向两个大小都是的初速度，由于这两个方向相反的速度的合速度为零，因而不影响带电质点以后的运动．在时刻，带电质点因具有沿轴正方向的初速度而受洛伦兹力的作用。

                                                           （2）

其方向与重力的方向相反．适当选择的大小，使等于重力，即

                                                          （3）

                                               (4)

只要带电质点保持（4）式决定的沿轴正方向运动，与重力的合力永远等于零．但此时，位于坐标原点的带电质点还具有竖直向下的速度和沿轴负方向的速度，二者的合成速度大小为

                                             （5）

方向指向左下方，设它与轴的负方向的夹角为，如图复解17-5-1所示，则

                   

                               （6）

因而带电质点从时刻起的运动可以看做是速率为，沿轴的正方向的匀速直线运动和在平面内速率为的匀速圆周运动的合成．圆周半径

                      （7）

带电质点进入磁场瞬间所对应的圆周运动的圆心位于垂直于质点此时速度的直线上，由图复解17-5-1可知，其坐标为

                                              （8） 

圆周运动的角速度

                                                 （9）

由图复解17-5-1可知，在带电质点离开磁场区域前的任何时刻，质点位置的坐标为

                                         （10）

                                              （11）

式中、、、、、已分别由（4）、（7）、（9）、（6）、（8）各式给出。

带电质点到达磁场区域下边界时，，代入（11）式，再代入有关数值，解得

                                                      （12）

将（12）式代入（10）式，再代入有关数值得

                                                         （13）

所以带电质点离开磁场下边界时的位置的坐标为

                                           （14）

带电质点在磁场内的运动可分解成一个速率为的匀速圆周运动和一个速率为的沿轴正方向的匀速直线运动，任何时刻，带电质点的速度便是匀速圆周运动速度与匀速直线运动的速度的合速度．若圆周运动的速度在方向和方向的分量为、，则质点合速度在方向和方向的分速度分别为

          

                                         （15）

                                                         （16）

虽然，由（5）式决定，其大小是恒定不变的，由（4）式决定，也是恒定不变的，但在质点运动过程中因的方向不断变化，它在方向和方向的分量和都随时间变化，因此和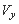也随时间变化，取决于所考察时刻质点做圆周运动速度的方向，由于圆周运动的圆心的坐标恰为磁场区域宽度的一半，由对称性可知，带电质点离开磁场下边缘时，圆周运动的速度方向应指向右下方，与轴正方向夹角，故代入数值得

               

               

将以上两式及（5）式代入（15）、（16）式，便得带电质点刚离开磁场区域时的速度分量，它们分别为

                                                     （17）

                                                     （18）

速度大小为

                （19）

设的方向与轴的夹角为，如图复解17-5-2所示，则

       

得                              （20）

评分标准：本题25分

（4）式5分，求得（5）、（6）式各给3分，求得（10）、（11）式各给2分，（14）式3分，（19）式5分，求得（20）式再给2分。

解法二：

若以带电质点到达坐标原点的时刻作为起始时刻（），则质点的初速度为

                                         （1¢）

方向沿轴正方向．进入磁场区后，带电质点将受到洛伦兹力作用，洛伦兹力在方向的分力取决于质点在方向的分速度，因此质点动量在方向的分量的增量为

                               （2¢）

是带电质点在时间内沿方向的位移，质点在磁场中运动的整个过程中，此式对每一段时间都成立，所以在到时间内方向的动量的改变为

               

因初始时刻（），带电质点在轴方向的动量为零，其位置在原点，，因而得

               

即                                                        （3¢）

    当带电质点具有方向的速度后，便立即受到沿负方向的洛伦兹力的作用．根据牛顿第二定律，在方向上有加速度

                                                    （4¢）

将（3¢）式代入（4¢）式，得

                                         （5¢）

令                                                        （6¢）

式中

                                       （7¢）

即在方向作用于带电质点的合力

               

其中           

是准弹性力，在作用下，带电质点在方向的运动是简谐振动，振动的圆频率

                                             （8¢）

随时间变化的规律为

                                                   （9¢）      

或

                                               （10¢）

与是待求的常量，质点的简谐运动可以用参考圆来描写，以所考察的简谐运动的振幅为半径作一圆，过圆心作一直角坐标．若有一质点沿此圆周做匀速率圆周运动，运动的角速度等于所考察简谐运动的角频率，且按逆时针方向转动，在时刻，点的在圆周上的位置恰使连线与轴的夹角等于（9¢）式中的常量，则在任意时刻，与的连线与轴的夹角等于，于是连线在轴上的投影即为（9¢）式所示的简谐振动，将轴平行下移，连线在轴的投影即如（10¢）式所示（参看图复解17-5-3），点做圆周运动的速度大小，方向与垂直，速度的分量就是带电质点沿轴做简谐运动的速度，即

                                                （11¢）

（10¢）和（11¢）两式中的和可由下面的方法求得：因为已知在时，带电质点位于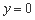处，速度，把这个条件代入（10¢）式与（11¢）式得

               

               

解上面两式，结合(1¢)、(8¢)式，注意到振幅总是正的，故得
                                                            (12¢)

                                                          (13¢)

把（10¢）式代入(3¢)式，便得带电质点沿轴运动的速度

                                             (14¢)

（14¢）式表示带电质点在方向上的速度是由两个速度合成的，即沿方向的匀速运动速度和方向的简谐振动速度的合成，带电质点沿方向的匀速运动的位移

                                                           （15¢）

由沿方向的简谐振动速度可知，沿方向振动位移的振幅等于速度的最大值与角频率的比值（参看图复解17-5-3），即等于．由参考圆方法可知，沿方向的振动的位移具有如下的形式

               

它可能是，亦可能是．在本题中，时刻，应为零，故前一表示式不符合题意．后一表示式中，应取的值为，故有

                                          （16¢）

带电质点在方向的合位移，由（15¢）、（16¢）式，得

                      （17¢）

（17¢）、（10¢）、（14¢）和（11¢）式分别给出了带电质点在离开磁场区域前任何时刻的位置坐标和速度的分量和分量，式中常量、、、已分别由（8¢）、（13¢）、（12¢）和（7¢）式给出．
    当带电质点达到磁场的下边界时，

                                      （18¢）

将与（10¢）式有关的数据代入（10¢）式，可解得

                                            （19¢）

代入（17¢）式，得

                                           （20¢）

将（19¢）式分别代入（14¢）式与（11¢）式，得

                     

速度大小为

                                                   （21¢）

速度方向为

                                                       （22¢）

评分标准：本题25分

（7¢）式2分，（8¢）式3分，（10¢）式2分，（11¢）式2分，（12¢）式3分，（13¢）式3分，（14¢）式2分，（17¢）式3分，（20¢）式3分，（21¢）式1分，（22¢）式1分。