

���� ��1������ԭ��ͼ�ɵó���Ӧ��ʵ��ͼ��
��2��������÷��跨���Դ�ĵ綯�ƺ����裬�ɱպϵ�·ŷķ���ɿɵó�����ʽ����ɵó�ͼ���н�������壻
��3������ͼ��ͱ���ʽ����ͼ����������Ľ������õ�Դ�ĵ綯�ƣ���ͼ���б�ʿ�����ڵ��裮
��� 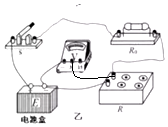 �⣺��1������ԭ��ͼ�ɵó���ȷ��ʵ��ͼ��ͼ��ʾ��
�⣺��1������ԭ��ͼ�ɵó���ȷ��ʵ��ͼ��ͼ��ʾ��
��2���ɱպϵ�·ŷķ���ɿ�֪��
U=$\frac{E}{R+R_{0}+r}$R
���οɵã�$\frac{1}{U}$=$\frac{R+r+R_{0}}{ER}$=$\frac{R_{0}+r}{ER}$+$\frac{1}{E}$
�ʱ���ʽΪ��$\frac{1}{U}$=$\frac{R_{0}+r}{ER}$+$\frac{1}{E}$
����ѧ֪ʶ��֪��ͼ����������Ľ���Ϊ��Դ�綯�Ƶĵ�����
��2����ͼ��֪��ͼ����������Ľ���Ϊ��0.35=$\frac{1}{E}$��
��ã�E=2.9V��
ͼ���б��Ϊ��k=$\frac{2.95-0.35}{1.0}$=2.6
$\frac{R_{0}+r}{E}$=2.6
��ã�r=2.5��
�ʴ�Ϊ����1����ͼ��ʾ����2��$\frac{1}{U}$=$\frac{R_{0}+r}{ER}$+$\frac{1}{E}$����3��2.9��2.5��
���� ���⿼��ʹ�÷��跨�ⶨ�綯�ƺ��ڵ����ʵ�飬ע����ݱպϵ�·ŷķ������ñ���ʽ���ٽ��ͼ������弴�ɵó��綯�ƺ��ڵ��裻��Ҫ�����ڱ���ʽ�ı��ι�����ע����ѧ֪ʶ��Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 2.5 m/s2 | B�� | 4 m/s2? | C�� | 5.5 m/s2 | D�� | 7 m/s2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �����ۡ��������е����ļ��ٶȴ���ͬ�����ǵ����ļ��ٶ� | |
| B�� | �����ۡ�������Բ����ϵ��������ʴ���ͬ�����ǵ����� | |
| C�� | �����ۡ�������Բ����ϵ����н��ٶ�С��ͬ�����ǵĽ��ٶ� | |
| D�� | �����ۡ���������ʱ�����ĸ߶�С��ͬ�����ǵĸ߶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
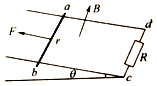 ��ͼ��ʾ���̶������Ϊ��=30���б���ڵ�����ƽ�г�ֱ�⻬��������ļ��Ϊd=l m����˽�����ֵΪR=2���ĵ��裬����װ�ô��ڴ�ֱб�����ϡ��Ÿ�Ӧǿ�ȴ�СΪB=2T����ǿ�ų��У�һ����Ϊm=l kg�������ֲ����ȣ��ĵ����ab��ֱ�ڵ�����ã����������챣�����ýӴ����ָ�����б�����ϡ���ֱ�ڸ˵ĺ���F=10N�����´Ӿ�ֹ��ʼ�ص��������˶�����L=6mʱ���ٶ�ǡ�ôﵽ����˶������и�ʼ���뵼�챣�ִ�ֱ������˽��˵�·�ĵ���Ϊr=2����������費�ƣ��������ٶȴ�СΪg=10 m/s2����˹��̣�������
��ͼ��ʾ���̶������Ϊ��=30���б���ڵ�����ƽ�г�ֱ�⻬��������ļ��Ϊd=l m����˽�����ֵΪR=2���ĵ��裬����װ�ô��ڴ�ֱб�����ϡ��Ÿ�Ӧǿ�ȴ�СΪB=2T����ǿ�ų��У�һ����Ϊm=l kg�������ֲ����ȣ��ĵ����ab��ֱ�ڵ�����ã����������챣�����ýӴ����ָ�����б�����ϡ���ֱ�ڸ˵ĺ���F=10N�����´Ӿ�ֹ��ʼ�ص��������˶�����L=6mʱ���ٶ�ǡ�ôﵽ����˶������и�ʼ���뵼�챣�ִ�ֱ������˽��˵�·�ĵ���Ϊr=2����������費�ƣ��������ٶȴ�СΪg=10 m/s2����˹��̣�������| A�� | �˵��ٶ����ֵΪ5m/s | |
| B�� | ��������R�ĵ���Ϊ6C | |
| C�� | ����һ�����У�������·�����Ľ�����Ϊ17.5 J | |
| D�� | ��������R����������c��d |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���ٶ�С | B�� | ���ٶȴ� | C�� | ��������С | D�� | ���ļ��ٶȴ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����������Ԫ���e����ֵ | |
| B�� | ¬ɪ��ͨ��������ɢ��ʵ�齨����ԭ�ӵĺ�ʽ�ṹģ�� | |
| C�� | ԭ�Ӻ˷���˥��ʱҪ�ͷ�����������E=mc2������˥������������Ҫ���� | |
| D�� | ��������˷��ӵ�����˵ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | Ƶ��Խ��Ĺ⣬����ӵ�����ԽС | |
| B�� | Ƶ��Խ��Ĺ⣬����ӵĶ���Խ�� | |
| C�� | ����������ۡ���Ϊ�����˶����ٶ�Խ������ԽС | |
| D�� | ����������ۡ���Ϊ�����˶����ٶ�Խ������ԽС |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ������ϵ��Ϊk���ᵯ�ɵ�һ�˹̶���ǽ�ϣ���һ��������ˮƽ���ϵ�������Ϊm������A��B�Ӵ���A��B�͵��ɾ�δ���ӣ�������ˮƽ�����α䣮��ˮƽ��F�������ƶ�����B���ڵ������ڵ��ɳ��ȱ�ѹ����x0�����ɵ�������Ϊ$\frac{1}{2}$kx02����ʱ����A��B��ֹ����֪����A��ˮƽ���Ķ�Ħ������Ϊ�̣�����B��ˮƽ����Ħ�����ƣ���ȥ��F������A��B��ʼ�����˶���A�˶���������Ϊ4x0���������ٶ�Ϊg��������
��ͼ��ʾ������ϵ��Ϊk���ᵯ�ɵ�һ�˹̶���ǽ�ϣ���һ��������ˮƽ���ϵ�������Ϊm������A��B�Ӵ���A��B�͵��ɾ�δ���ӣ�������ˮƽ�����α䣮��ˮƽ��F�������ƶ�����B���ڵ������ڵ��ɳ��ȱ�ѹ����x0�����ɵ�������Ϊ$\frac{1}{2}$kx02����ʱ����A��B��ֹ����֪����A��ˮƽ���Ķ�Ħ������Ϊ�̣�����B��ˮƽ����Ħ�����ƣ���ȥ��F������A��B��ʼ�����˶���A�˶���������Ϊ4x0���������ٶ�Ϊg��������| A�� | ��ȥF������A�����ȼ����˶��������ȼ����˶� | |
| B�� | ��ȥF��������˶�ʱ�ļ��ٶȴ�СΪ$\frac{k{x}_{0}}{m}-��g$ | |
| C�� | ����A��Bһ�������˶����˶�����x0-$\frac{��mg}{k}$��A��B�ֿ� | |
| D�� | ����A��B�ֿ���˲�䣬����A���ٶ�Ϊ$\sqrt{\frac{k{{x}_{0}}^{2}}{m}-4��g{x}_{0}}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com