
分析 根据速度时间公式求出1s后的竖直分速度,结合平行四边形定则得出平抛运动的初速度.再根据平行四边形定则得出落到时的竖直分速度,结合速度位移公式求出抛出点的高度,根据速度时间公式求出物体在空中运动的时间.
解答 解:1s后竖直分速度vy1=gt1=10×1m/s=10m/s,
根据平行四边形定则知,tan45°=$\frac{{v}_{y1}}{{v}_{0}}$,
解得v0=vy1=10m/s.
落地时,根据$tan60°=\frac{{v}_{y2}}{{v}_{0}}$得,${v}_{y2}=\sqrt{3}{v}_{0}=10\sqrt{3}m/s$,
抛出点到地面的高度h=$\frac{{{v}_{y2}}^{2}}{2g}=\frac{300}{20}m=15m$,
物体在空中运动的时间t=$\frac{{v}_{y2}}{g}=\frac{10\sqrt{3}}{10}s=\sqrt{3}s$.
答:抛出点到地面的高度为15m,物体在空中运动的时间为$\sqrt{3}$s.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和平行四边形定则灵活求解.


科目:高中物理 来源: 题型:选择题
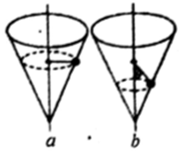 在光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小 环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内做水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图a中小环与小球在同一水平面上,图b中轻绳与竖直轴成θ(θ<90°)角,设图a和图b中轻绳对小球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则在下列说法中正确的是( )
在光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小 环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内做水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图a中小环与小球在同一水平面上,图b中轻绳与竖直轴成θ(θ<90°)角,设图a和图b中轻绳对小球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则在下列说法中正确的是( )| A. | Ta-定为零,Tb一定为零 | |
| B. | Ta、Tb是否为零取决于小球速度的大小 | |
| C. | Na可以为零,Nb一定不为零 | |
| D. | Na、Nb的大小与小球的速度无关 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图,静止于光滑水平地面上的木板质量为M、长度为l,叠放在木板上的滑块质量为m,一轻绳通过光滑定滑轮分别与木板和滑块连接,滑块与木板间的动摩擦因数为μ,开始时滑块静止在木板左端,现用水平向右的拉力F将滑块拉至木板右端,则滑块运动到木板右端的时间为( )
如图,静止于光滑水平地面上的木板质量为M、长度为l,叠放在木板上的滑块质量为m,一轻绳通过光滑定滑轮分别与木板和滑块连接,滑块与木板间的动摩擦因数为μ,开始时滑块静止在木板左端,现用水平向右的拉力F将滑块拉至木板右端,则滑块运动到木板右端的时间为( )| A. | $\sqrt{\frac{2(M+m)l}{F-2μmg}}$ | B. | $\sqrt{\frac{(M+m)l}{2(F-2μmg)}}$ | C. | $\sqrt{\frac{(M+m)l}{F-2μmg}}$ | D. | $\sqrt{\frac{2(M+m)l}{F-μmg}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
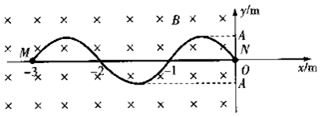 如图所示,在y轴左侧有垂直坐标平面向里的匀强磁场,一个弯曲成正弦曲线的漆包线(表面涂有绝缘漆的铜导线)和一直导线焊接而成的线圈按如图所示放置,N点与坐标原点重合,线圈处于坐标平面内.已知磁感应强度B=1T,直导线 LMN=3m,正弦曲线的振幅A=0.3m,两焊点M、N的电阻均为R=0.2Ω,其余部分电阻不计.某时刻给线圈一个作用力F使其沿x轴正方向以速度v=2m/s匀速离开磁场.试求:
如图所示,在y轴左侧有垂直坐标平面向里的匀强磁场,一个弯曲成正弦曲线的漆包线(表面涂有绝缘漆的铜导线)和一直导线焊接而成的线圈按如图所示放置,N点与坐标原点重合,线圈处于坐标平面内.已知磁感应强度B=1T,直导线 LMN=3m,正弦曲线的振幅A=0.3m,两焊点M、N的电阻均为R=0.2Ω,其余部分电阻不计.某时刻给线圈一个作用力F使其沿x轴正方向以速度v=2m/s匀速离开磁场.试求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
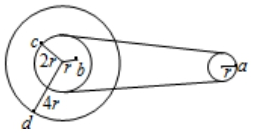 图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( )
图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到小轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若在传动过程中,皮带不打滑.则( )| A. | c点与d点的角速度大小相等 | B. | a点与b点的角速度大小相等 | ||
| C. | d点与b点的线速度大小相等 | D. | a点与c点的线速度大小相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com