
 ��ͼ1��ʾ������ϵ��Ϊk���ᵯ����ֱ���ã��¶˹̶���ˮƽ�����ϣ�һ����Ϊm��С���뵯���϶˸�h�������ͷţ�ѹ�ϵ��ɺ��� ����һ���˶�������С��ʼ�����λ��Ϊԭ�㣬����ֱ���½�һ����ϵox����С����ٶ�v2��x�ı仯ͼ����ͼ2��ʾ������OA��Ϊֱ�ߣ�AB������OA������A������ߣ�BC��ƽ�������ߣ������A��B��C����� Ӧ��λ�����꼰���ٶȣ�����˵����ȷ���ǣ�������
��ͼ1��ʾ������ϵ��Ϊk���ᵯ����ֱ���ã��¶˹̶���ˮƽ�����ϣ�һ����Ϊm��С���뵯���϶˸�h�������ͷţ�ѹ�ϵ��ɺ��� ����һ���˶�������С��ʼ�����λ��Ϊԭ�㣬����ֱ���½�һ����ϵox����С����ٶ�v2��x�ı仯ͼ����ͼ2��ʾ������OA��Ϊֱ�ߣ�AB������OA������A������ߣ�BC��ƽ�������ߣ������A��B��C����� Ӧ��λ�����꼰���ٶȣ�����˵����ȷ���ǣ�������| A�� | xA=h��aA=g | B�� | xB=h��aB=g | C�� | xB=$h+\frac{mg}{k}$��aB=0 | D�� | xC=$h+\frac{mg}{k}$��aC��g |
���� ��С��OA����ֱ�߿���֪��������ٶȺ㶨���ʴ˶δ���С��Ӵ�����ǰ���˶����ʶ�����֪��A���λ������Ϊh����ͼ֪B����ٶ�Ϊ�㣬�ȴ�ʱ�����������������ɴ˿�����õ����α������̶�����֪��B�����꣮��D����ٶ�Ϊ�㣬�����ɱ�ѹ��������ɴ˿���֪��ʱ���������������ʶ��˵�ļ��ٶ�һ�������㣮
��� �⣺A����С��OA����ֱ�߿���֪��������ٶȺ㶨���ʴ˶δ���С��Ӵ�����ǰ�����������˶����ʶ�����֪��A���λ������Ϊh�����ٶ�Ϊ�������ٶȣ���A��ȷ��
B����ͼ֪B����ٶ�Ϊ�㣬�ȴ�ʱ����������������ʱ�����α���Ϊ��$��x=\frac{mg}{k}$����B������Ϊ��${x}_{B}=h+\frac{mg}{k}$����B����C��ȷ��
D��С���B����������������˶����ʶ�C�������Ӧ����B������꣬��D����
��ѡ��C��
���� �����ѵ�һ�Ƕ�ͼ���ʶ������⣬������ͼ�����С��ļ��������˶��Σ�������С�ɵ�һ���Ϊ�����Σ��������壬����С���������������������������˶����ʲ�һ����Ӧע�����գ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����ֻ��ѹ����Ϊ�����ѹ������ֵ����R1�ͻ���������R2��������Դ���費�ܺ��ԣ��ֽ������������Ļ�Ƭ�����ƶ�����һλ�ã����ֵ�ѹ��V3��ʾ��������0.30V�����ѹ��Vl��V2��ʾ���仯�����ǣ�������
��ͼ��ʾ����ֻ��ѹ����Ϊ�����ѹ������ֵ����R1�ͻ���������R2��������Դ���費�ܺ��ԣ��ֽ������������Ļ�Ƭ�����ƶ�����һλ�ã����ֵ�ѹ��V3��ʾ��������0.30V�����ѹ��Vl��V2��ʾ���仯�����ǣ�������| A�� | V1��С0.20V��V2����0.50V | B�� | V1����0.10V��V2����0.20V | ||
| C�� | V1��С0.10V��V2��С0.20V | D�� | V1����0.20V��V2����0.10V |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ�����е�������ͬ�ģ�����״���������ֲ����ȣ�������ڹ⻬б��⻬ˮƽ��֮�䣬���������Ҳ������Ӵ������ڹ⻬��ˮƽ���ϣ����������Ҳ���������һ����Ĺ⻬����ڲ�����Ӵ���һѧ������������б̨��ʾ��ͼ��ͼ���������ĸ�����������������˵����ȷ���ǣ�������
��ͼ��ʾ�����е�������ͬ�ģ�����״���������ֲ����ȣ�������ڹ⻬б��⻬ˮƽ��֮�䣬���������Ҳ������Ӵ������ڹ⻬��ˮƽ���ϣ����������Ҳ���������һ����Ĺ⻬����ڲ�����Ӵ���һѧ������������б̨��ʾ��ͼ��ͼ���������ĸ�����������������˵����ȷ���ǣ�������| A�� | �����ܵ��������������� | |
| B�� | �����ܵ�һ������������ | |
| C�� | �����ܵ��������������� | |
| D�� | ����������б̨����ʱб̨������ĵ�����������v1�ķ������v2�ķ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ����10N������λ����Ǧ�=30���б���ϣ�����б�����ϵ�F=6N���������´��ھ�ֹ״̬����б��������Ħ������С�Ƕ��٣��������������F�ֱ�Ϊ4N��5N��Ħ�����Ĵ�С��������������
��ͼ��ʾ����10N������λ����Ǧ�=30���б���ϣ�����б�����ϵ�F=6N���������´��ھ�ֹ״̬����б��������Ħ������С�Ƕ��٣��������������F�ֱ�Ϊ4N��5N��Ħ�����Ĵ�С���������������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
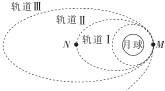 ���ſƼ��ķ�չ��δ���ҹ���̽�������̽�����ڿ�����ɺ��ص����������ͼ��ʾ���й�̽��������������˵����ȷ���ǣ�������
���ſƼ��ķ�չ��δ���ҹ���̽�������̽�����ڿ�����ɺ��ص����������ͼ��ʾ���й�̽��������������˵����ȷ���ǣ�������| A�� | ̽�����ڹ�����ϵĻ�е�ܴ��ڹ��I�ϵĻ�е�� | |
| B�� | ̽�����ڹ��I�����������е�������̽������ͬ���Ĺ�����Ƶ������е�������� | |
| C�� | ̽�����ڹ�����Ͼ���M��ļ��ٶ�С��̽�����ڹ��I�Ϲ�M��ļ��ٶ� | |
| D�� | ̽�����ڹ�����Ϲ�M����ٶȴ��ڹ�N����ٶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ���뾶ΪR�İ������չޣ��̶��ڿ�������ֱ����ת��ˮƽת̨�ϣ�ת̨ת������չ�����O�ĶԳ���OO���غϣ�ת̨��һ�����ٶȦ�����ת����һ����Ϊm��С��������չ��ڣ�����һ��ʱ���С������չ�һ��ת������Թޱھ�ֹ������O���������OO��֮��ļнǦ�Ϊ53�㣬������մɼ�Ķ�Ħ������Ϊ0.5���������ٶȴ�СΪg��sin53��=0.8��cos53��=0.6��������
��ͼ��ʾ���뾶ΪR�İ������չޣ��̶��ڿ�������ֱ����ת��ˮƽת̨�ϣ�ת̨ת������չ�����O�ĶԳ���OO���غϣ�ת̨��һ�����ٶȦ�����ת����һ����Ϊm��С��������չ��ڣ�����һ��ʱ���С������չ�һ��ת������Թޱھ�ֹ������O���������OO��֮��ļнǦ�Ϊ53�㣬������մɼ�Ķ�Ħ������Ϊ0.5���������ٶȴ�СΪg��sin53��=0.8��cos53��=0.6��������| A�� | ��С����ܵ�Ħ����Ϊ��ʱ��С�����������֧���������������� | |
| B�� | ���Ž��ٶȦص�����С����ܵ�Ħ���������� | |
| C�� | ʹС��鲻�»�����С���ٶ�Ϊ��=$\sqrt{\frac{5g}{6R}}$ | |
| D�� | �����ٶȦ�=$\sqrt{\frac{5g}{3R}}$ʱС����ܵ���Ħ����Ϊ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{4��}{{G{T^2}}}$ | B�� | $\frac{3��}{{G{T^2}}}$ | C�� | $\frac{2��}{{G{T^2}}}$ | D�� | $\frac{��}{{G{T^2}}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{R_0^3{T^2}}}{{{R^3}T_0^2}}$ | B�� | $\frac{{{R^3}T_0^2}}{{R_0^3{T^2}}}$ | ||
| C�� | $1-\frac{{R_0^3{T^2}}}{{{R^3}T_0^2}}$ | D�� | $1-\frac{{{R^3}T_0^2}}{{R_0^3{T^2}}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ����������ȵ�����С�����ң����������ӣ������������Բ��ƣ�����ֹ�ں����ϣ����Ҵ��ڵ�����һ���㶨�����������ӣ���ͼ��ʾ�����ˮ���������ƣ������ж�����ȷ���ǣ�������
����������ȵ�����С�����ң����������ӣ������������Բ��ƣ�����ֹ�ں����ϣ����Ҵ��ڵ�����һ���㶨�����������ӣ���ͼ��ʾ�����ˮ���������ƣ������ж�����ȷ���ǣ�������| A�� | �������ӵ������ڼ����ӵ����� | |
| B�� | ���ӶԼ����������Ӷ��˵��������������뷴������ | |
| C�� | ���ӶԼ����������Ӷ��˵���������Ч���ܹ����� | |
| D�� | ���������˶����һ�õļ��ٶ�ҪС�ڼ�õļ��ٶ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com