
 =17.25J,弹簧一端固定在底端,与小滑块不相连,弹簧原长为2.05m,轨道与滑块间的动摩擦因数
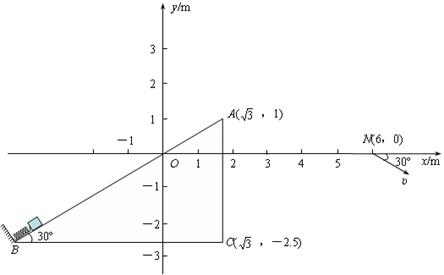
=17.25J,弹簧一端固定在底端,与小滑块不相连,弹簧原长为2.05m,轨道与滑块间的动摩擦因数 .某时刻撤去外力,经过一段时间弹簧恢复至原长,再经过1.8s,同时施加电场和磁场,电场平行于纸面,且垂直x轴向上,场强E=10N/C;磁场方向垂直于纸面,且仅存在于第二、三象限内,最终滑块到达N(6m,0)点,方向与水平方向成30º斜向下.(答案可用π表示,
.某时刻撤去外力,经过一段时间弹簧恢复至原长,再经过1.8s,同时施加电场和磁场,电场平行于纸面,且垂直x轴向上,场强E=10N/C;磁场方向垂直于纸面,且仅存在于第二、三象限内,最终滑块到达N(6m,0)点,方向与水平方向成30º斜向下.(答案可用π表示, )
)
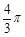 s
s 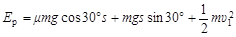 (2分)
(2分)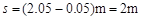
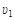 =7.5m/s (1分)
=7.5m/s (1分)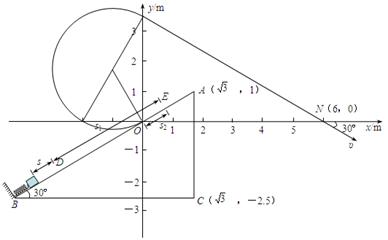
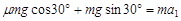 (2分)
(2分) =7.5
=7.5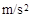 (1分)
(1分)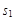 ,则运动时间为:
,则运动时间为: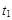 =
=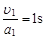 (1分)
(1分)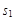 =
=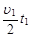 =3.75m (1分)
=3.75m (1分)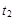 =(1.8-1)s=0.8s
=(1.8-1)s=0.8s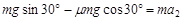 (1分)
(1分)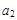 =2.5
=2.5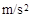 (1分)
(1分)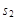 =
=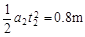 (1分)
(1分)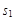 =BO+
=BO+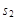 (1分)
(1分)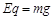
 m)点,然后做匀速直线运动运动到N(6m,0).
m)点,然后做匀速直线运动运动到N(6m,0).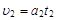 =2m/s
=2m/s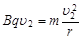 (2分)
(2分)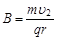 =1T (1分)
=1T (1分)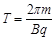
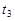 =
=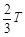 =
=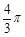 s (1分)
s (1分)

科目:高中物理 来源:不详 题型:计算题

查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题


 试推导出电子比荷
试推导出电子比荷 的表达式;
的表达式;查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题
 ,0),在y轴与直线MN之间的区域内,存在垂直于xOy平面向外、磁感应强度为B的匀强磁场。在直角坐标系xOy的第Ⅳ象限区域内存在沿y轴,正方向、大小为
,0),在y轴与直线MN之间的区域内,存在垂直于xOy平面向外、磁感应强度为B的匀强磁场。在直角坐标系xOy的第Ⅳ象限区域内存在沿y轴,正方向、大小为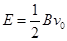 的匀强电场,在x=3a处垂直于x轴放置一平面荧光屏,与x轴交点为Q,电子束以相同的速度v0从y轴上0
的匀强电场,在x=3a处垂直于x轴放置一平面荧光屏,与x轴交点为Q,电子束以相同的速度v0从y轴上0 y
y 2a的区间垂直于y轴和磁场方向射入磁场。已知从y=2a点射入的电子在磁场中轨迹恰好经过O点,忽略电子间的相互作用,不计电子的重力。求:
2a的区间垂直于y轴和磁场方向射入磁场。已知从y=2a点射入的电子在磁场中轨迹恰好经过O点,忽略电子间的相互作用,不计电子的重力。求: ;
;
查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题
 .现将一质量为m、带电量为-q(q>0)的小环套在PQ杆上,小环所受的电场力大小为其重力的3倍.(重力加速度为g).求:
.现将一质量为m、带电量为-q(q>0)的小环套在PQ杆上,小环所受的电场力大小为其重力的3倍.(重力加速度为g).求:
查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题
 )d,板间距离为2d,在两板间有一圆形匀强磁场区域,磁场边界与两板及右侧边缘线相切,P点是磁场边界与下板N的切点,磁场方向垂直于纸面向里,现有一带电微粒从板的左侧进入磁场,若微粒从两板的正中间以大小为v0水平速度进入板间电场,恰做匀速直线运动,经圆形磁场偏转后打在P点。
)d,板间距离为2d,在两板间有一圆形匀强磁场区域,磁场边界与两板及右侧边缘线相切,P点是磁场边界与下板N的切点,磁场方向垂直于纸面向里,现有一带电微粒从板的左侧进入磁场,若微粒从两板的正中间以大小为v0水平速度进入板间电场,恰做匀速直线运动,经圆形磁场偏转后打在P点。
查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题

查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题

查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题
 后进入Ⅱ区.已知Ⅰ区的磁感应强度的大小为B,Ⅱ区的电场强度大小为2Bv0,不计粒子重力.求:
后进入Ⅱ区.已知Ⅰ区的磁感应强度的大小为B,Ⅱ区的电场强度大小为2Bv0,不计粒子重力.求:
 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com