
 如图所示,A、B是一对平行的金属板,在两板间加上一周期为T的交变电压.B板的电势φB=0,A板的电势φA随时间的变化规律为:在0~$\frac{T}{2}$时间内φA=U(正的常量);在$\frac{T}{2}$~T时间内φA=-U.现有一电荷量为q、质量为m的带负电粒子从B板上的小孔S处进入两板间的电场区内,设粒子的初速度和重力均可忽略.
如图所示,A、B是一对平行的金属板,在两板间加上一周期为T的交变电压.B板的电势φB=0,A板的电势φA随时间的变化规律为:在0~$\frac{T}{2}$时间内φA=U(正的常量);在$\frac{T}{2}$~T时间内φA=-U.现有一电荷量为q、质量为m的带负电粒子从B板上的小孔S处进入两板间的电场区内,设粒子的初速度和重力均可忽略.分析 (1)电子在t=0时刻进入时,在一个周期内,前半个周期受到的电场力向上,向上做加速运动,后半个周期受到的电场力向下,继续向上做减速运动,T时刻速度为零,接着周而复始,所以电子一直向B板运动,做出v-t图象进行分析,根据牛顿第二定律和运动学公式列式求解;
(2)若粒子是在t=$\frac{T}{8}$时刻进入的,在上一副图上继续做出v-t图象分析,注意v-t图象与时间轴包围的面积表示位移大小;
(3)若粒子是在t=$\frac{3T}{8}$时刻进入的,同样做出v-t图象进行分析即可.
解答 解:(1)0-$\frac{T}{2}$内,向上做匀加速直线运动,加速度为:a=$\frac{qU}{m{d}_{1}}$;
位移为:y1=$\frac{1}{2}a{t}^{2}=\frac{1}{2}×\frac{qU}{m{d}_{1}}×(\frac{T}{2})^{2}$;
结合分析中内容“在一个周期内,前半个周期受到的电场力向上,向上做加速运动,后半个周期受到的电场力向下,继续向上做减速运动,T时刻速度为零,接着周而复始“,做出v-t图象,如图所示: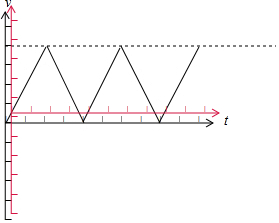
故前2T内的位移:y=4y1=d1;
联立解得:d1=$\sqrt{\frac{qU{T}^{2}}{2m}}$;
(2)若粒子是在t=$\frac{T}{8}$时刻进入的,且经过$\frac{11T}{8}$时间恰好到达A板,画出v-t图象,如上图中红色的坐标轴所示:
v-t图象与时间轴包围的面积表示位移大小,故:
d2=$\frac{1}{2}a(\frac{3}{8}T)^{2}×2-\frac{1}{2}a(\frac{T}{8})^{2}×2+\frac{1}{2}a(\frac{2}{8}T)^{2}$=$\frac{21}{128}a{T}^{2}$=$\frac{21}{128}•\frac{qU}{m{d}_{2}}•{T}^{2}$,
解得:d2=$\sqrt{\frac{21qU{T}^{2}}{128m}}$;
(3)若粒子是在t=$\frac{3T}{8}$时刻进入的,做出v-t图象,如图所示:
显然在$\frac{3}{8}T-\frac{T}{2}$向上匀加速运动,$\frac{T}{2}-\frac{5}{8}T$向上匀减速,$\frac{5}{8}T$开始向下匀加速,直到离开电场,根据位移公式,有:
0=$\frac{1}{2}a(\frac{T}{8})^{2}$×2-$\frac{1}{2}a{t}^{2}$
解得:t=$\frac{\sqrt{2}}{8}T$;
答:(1)若粒子是在t=0时刻进入的,且经过2T时间恰好到达A板,则A、B两板间距d1为$\sqrt{\frac{qU{T}^{2}}{2m}}$;
(2)若粒子是在t=$\frac{T}{8}$时刻进入的,且经过$\frac{11T}{8}$时间恰好到达A板,则A、B两板间距d2为$\sqrt{\frac{21qU{T}^{2}}{128m}}$;
(3)若粒子是在t=$\frac{3T}{8}$时刻进入的,且A、B两板间距足够大,则粒子经过$\frac{\sqrt{2}}{8}T$时间离开电场.
点评 本题粒子的运动具有周期性,关键是画出粒子运动的v-t图象,结合牛顿第二定律和运动学公式列式分析,较难.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中物理 来源: 题型:选择题
| A. | 掉在水泥地上的玻璃杯动量大,而掉在草地上的玻璃杯动量小 | |
| B. | 掉在水泥地上的玻璃杯动量改变大,掉在草地上的玻璃杯动量改变小 | |
| C. | 掉在水泥地上的玻璃杯动量改变慢,掉在草地上的玻璃杯动量改变快 | |
| D. | 掉在水泥地上的玻璃杯动量改变快,掉在草地上的玻璃杯动量改变慢 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
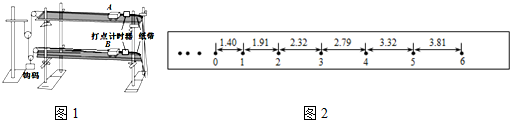
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
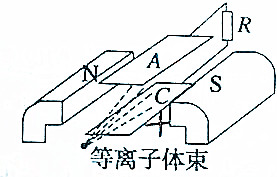 磁流体发电是一项新兴技术,它可把气体的内能直接转化为电能,如图所示是它的示意图,平行金属板A、C之间有一很强的磁场,将一束等离子体(即高温下电离的气体,含有大量正、负带电离子)喷入磁场,两板间便产生电压.现将A、C两极板与电阻R相连,两极板间距离为d,正对面积为S,等离子体的电阻率为ρ,磁感应强度为B,等离子体以速度v沿垂直磁场方向射入A、C两板之间,则稳定时下列说法中正确的是( )
磁流体发电是一项新兴技术,它可把气体的内能直接转化为电能,如图所示是它的示意图,平行金属板A、C之间有一很强的磁场,将一束等离子体(即高温下电离的气体,含有大量正、负带电离子)喷入磁场,两板间便产生电压.现将A、C两极板与电阻R相连,两极板间距离为d,正对面积为S,等离子体的电阻率为ρ,磁感应强度为B,等离子体以速度v沿垂直磁场方向射入A、C两板之间,则稳定时下列说法中正确的是( )| A. | 极板A是电源的正极 | B. | 电源的电动势为Bdv | ||
| C. | 极板A、C间电压大小为$\frac{BdvSR}{RS+ρd}$ | D. | 回路中电流为$\frac{Bdv}{R}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
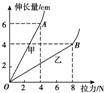 某同学要利用身边的粗细两种弹簧制作弹簧秤,为此首先各取一根弹簧进行了探究弹力和弹簧伸长量关系的实验,根据测得的数据绘出如图所示的图象,从图象上看:
某同学要利用身边的粗细两种弹簧制作弹簧秤,为此首先各取一根弹簧进行了探究弹力和弹簧伸长量关系的实验,根据测得的数据绘出如图所示的图象,从图象上看:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 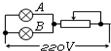 | B. |  | C. | 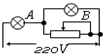 | D. | 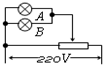 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com