
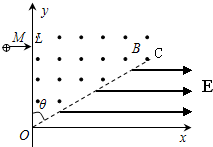
 如图所示,虚线OC与y轴的夹角θ=60°,在此角范围内有一方向垂直于xOy平面向外、磁感应强度大小为B的匀强磁场.虚线OC与x轴所夹范围内有一沿x轴正方向、电场强度大小为E的匀强电场.一质量为m、电荷量为q的带正电的粒子a(不计重力)从y轴的点M(0,L)沿x轴的正方向射入磁场中.求:
如图所示,虚线OC与y轴的夹角θ=60°,在此角范围内有一方向垂直于xOy平面向外、磁感应强度大小为B的匀强磁场.虚线OC与x轴所夹范围内有一沿x轴正方向、电场强度大小为E的匀强电场.一质量为m、电荷量为q的带正电的粒子a(不计重力)从y轴的点M(0,L)沿x轴的正方向射入磁场中.求:分析 (1)根据粒子的始末速度方向作出粒子在磁场中的运动轨迹,求得粒子圆周运动的轨道半径,据洛伦兹力提供向心力求得粒子的初速度和OP的距离;
(2)根据几何关系确定粒子在磁场中运动的最大圆心角和最小圆心角,据t=$\frac{θ}{2π}T$求得粒子射出的时间差.
解答 解:(1)粒子a竖直向下穿过OC,在磁场中轨迹圆心如图为O1,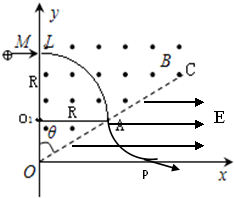
OO1=Rcotθ,OO1=L-R
得粒子圆周运动的轨道半径R=$\frac{3-\sqrt{3}}{2}L$ ①
由洛伦兹力提供圆周运动向心力有:
$q{v}_{1}B=m\frac{{v}_{1}^{2}}{R}$ ②
由①②两式解得:v1=$\frac{(3-\sqrt{3})qBL}{2m}$ ③
粒子a竖直向下穿过OC垂直进入匀强电场后,做类平抛运动,则有:
qE=ma
Rcotθ=v1t
解处t=$\frac{\sqrt{3}m}{3qB}$
$x=\frac{1}{2}a{t}^{2}$=$\frac{Em}{6q{B}^{2}}$
OP=R+x=$\frac{3-\sqrt{3}}{2}L+\frac{Em}{6q{B}^{2}}$
(2)由$q{v}_{2}B=m\frac{{v}_{2}^{2}}{{R}_{2}}$
解得:${R}_{2}=\frac{\sqrt{3}}{2}L$
粒子在磁场中做匀速圆周运动的周期为:$T=\frac{2π{R}_{2}}{{v}_{2}}=\frac{2πm}{qB}$
最后出磁场的粒子从OC边上的E点射出,弦ME最长为直径,ME=2R2=$\sqrt{3}L$,在磁场中运动的时间为:${t}_{1}=\frac{1}{2}T=\frac{πm}{qB}$ (11)
MF为垂直OC的一条弦,则MF为最短的弦,从F点射出的粒子运动时间最短,此时轨迹圆心为O2,由三角形关系得: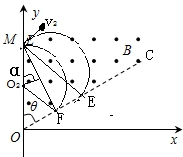
$MF=Lsinθ=\frac{\sqrt{3}}{2}L$,
sin$α=\frac{\frac{1}{2}MF}{{R}_{2}}=\frac{1}{2}$,
所以可得α=30°
此粒子的运动时间${t}_{2}=\frac{2α}{360°}T=\frac{πm}{3qB}$
时间差为△t=t1-t2=$\frac{2πm}{3qB}$
答:(1)要使粒子a从OC边界离开磁场后竖直向下垂直进入匀强电场,经过匀强电场后从x轴上的P点(图中未画出)离开,则该粒子射入磁场的初速度v1为$\frac{(3-\sqrt{3})qBL}{2m}$OP的距离为$\frac{3-\sqrt{3}}{2}L+\frac{Em}{6q{B}^{2}}$;
(2)若大量粒子a同时以v2=$\frac{\sqrt{3}qBL}{2m}$从M点沿xOy平面的各个方向射入磁场中,则从OC边界最先射出的粒子与最后射出的粒子的时间差为$\frac{2πm}{3qB}$.
点评 本题考查了求粒子做圆周运到达周期、运动时间等问题,难度较大,尤其是计算最长时间时,对数学能量的要求太高;根据几何关系求出带电粒子在磁场中的偏转角有两个,要注意分别进行求解.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 速度不断减小,然后反向加速,最后做匀速运动 | |
| B. | 速度不断减小,最后静止 | |
| C. | 速度不断减小,最后做匀速运动 | |
| D. | 速度一直增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
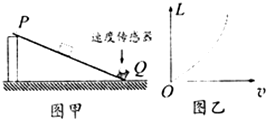 在做“探究做功和物体速度变化关系”的实验前,某探究小组的同学们通过讨论提出了以下几种猜想:①W∝υ,②W∝υ2,③W∝$\sqrt{υ}$,….
在做“探究做功和物体速度变化关系”的实验前,某探究小组的同学们通过讨论提出了以下几种猜想:①W∝υ,②W∝υ2,③W∝$\sqrt{υ}$,….查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 两细绳必须等长 | |
| B. | 弹簧秤、细绳、橡皮条都应与木板平行 | |
| C. | 两次将橡皮条和绳的结点拉到相同位置 | |
| D. | 两次将橡皮条拉伸相同长度即可 | |
| E. | 用两弹簧秤同时拉细绳时两弹簧秤夹角应适当大些 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 只有横波才能产生干涉,纵波不能产生干涉? | |
| B. | 只要是波都能产生稳定的干涉? | |
| C. | 不管是横波还是纵波,只要叠加的两列波的频率相等,振动情况相同就能产生稳定干涉? | |
| D. | 以上说法均不正确? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com