
 如图所示,两物体重分别为G1、G2,两弹簧劲度分别为k1、k2,弹簧两端与物体和地面相连,已知弹簧的弹力大小F=kx,式中x为弹簧的形变量,用竖直向上的力缓慢向上拉G2,最后平衡时拉力F=G1+2G2,求该过程G1、G2上升的高度.
如图所示,两物体重分别为G1、G2,两弹簧劲度分别为k1、k2,弹簧两端与物体和地面相连,已知弹簧的弹力大小F=kx,式中x为弹簧的形变量,用竖直向上的力缓慢向上拉G2,最后平衡时拉力F=G1+2G2,求该过程G1、G2上升的高度. 分析 开始时两个弹簧均处于压缩状态,根据胡克定律求解出两个弹簧的压缩量;用竖直向上的力缓慢向上拉G2,最后平衡时拉力F=G1+2G2时,两个弹簧都伸长,根据平衡条件和胡克定律绫求解出两弹簧的伸长量,最后结合空间几何关系得到G1、G2上升的高度.
解答 解:初始状态时k1弹簧的压缩量为 x1=$\frac{{G}_{1}+{G}_{2}}{{k}_{1}}$,k2弹簧的压缩量为 x2=$\frac{{G}_{2}}{{k}_{2}}$
末了状态时,由于F=G1+2G2>G1+G2,所以两根弹簧都处于伸长状态,k1、k2的伸长量分别为:
x1′=$\frac{{G}_{2}}{{k}_{1}}$,x2′=$\frac{{G}_{1}+{G}_{2}}{{k}_{2}}$
根据几何关系可得:该过程G1上升的高度 h1=x1+x1′=$\frac{{G}_{1}+2{G}_{2}}{{k}_{1}}$
G2上升的高度 h2=h2+(x2+x2′)=$\frac{{G}_{1}+2{G}_{2}}{{k}_{1}}$+$\frac{{G}_{1}+2{G}_{2}}{{k}_{2}}$=(G1+2G2)($\frac{1}{{k}_{1}}+\frac{1}{{k}_{2}}$)
答:G2上升的高度是(G1+2G2)($\frac{1}{{k}_{1}}+\frac{1}{{k}_{2}}$),G1上升的高度是$\frac{{G}_{1}+2{G}_{2}}{{k}_{1}}$.
点评 本题关键要正确判断弹簧的状态,分析上升高度与弹簧形变量的关系,根据平衡条件和胡克定律处理此类问题,


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
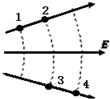 如图所示,实线表示某点电荷产生的电场线,虚线表示该电场的等势面,且1、2两点之间的距离等于3、4两点之间的距离.下列判断正确的是( )
如图所示,实线表示某点电荷产生的电场线,虚线表示该电场的等势面,且1、2两点之间的距离等于3、4两点之间的距离.下列判断正确的是( )| A. | 2、3两点的场强相同 | |
| B. | 1、2两点之间的电势差等于3、4两点之间的电势差 | |
| C. | 电子在1点的电势能小于在3点的电势能 | |
| D. | 把一正试探电荷从2移到4再移到3,电场力一直不做功 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量为m的球用细绳挂在质量为M的木块下,木块套在水平杆上,木块与杆间的动摩擦因式为μ,水平拉力F为多大时才能拉着球和木块一起做匀速运动,这时绳与水平方向的夹角α多大?
如图所示,质量为m的球用细绳挂在质量为M的木块下,木块套在水平杆上,木块与杆间的动摩擦因式为μ,水平拉力F为多大时才能拉着球和木块一起做匀速运动,这时绳与水平方向的夹角α多大?查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示的实验装置可以探究加速度与物体质量、物体受力的关系,小车上固定一个盒子,盒子内盛有沙子.沙桶的总质量(包括桶以及桶内沙子质量)记为m,小车的总质量(包括车、盒子及盒内沙子质量)记为M.
如图所示的实验装置可以探究加速度与物体质量、物体受力的关系,小车上固定一个盒子,盒子内盛有沙子.沙桶的总质量(包括桶以及桶内沙子质量)记为m,小车的总质量(包括车、盒子及盒内沙子质量)记为M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com