
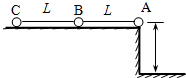
 如图所示,质量均为m的三个小球A、B、C用两条长为L的细线相连,置于高为h的光滑水平桌面上,L>h,A球刚跨过桌边,若A球、B球相继下落着地后均不再反弹,求:
如图所示,质量均为m的三个小球A、B、C用两条长为L的细线相连,置于高为h的光滑水平桌面上,L>h,A球刚跨过桌边,若A球、B球相继下落着地后均不再反弹,求:分析 (1)先对ABC三个物体分析,由机械能守恒可求得A落地时的速度;
(2)再对BC分析,由机械能守恒可得出C球离开桌面时的速度.
解答 解:(1)设B离开桌边的速度为vB,A球下落的过程中,A、B、C系统机械能守恒 得:
△EP=-mgh
又:$△{E_K}=3×\frac{1}{2}mv_B^2$
因为:△EP+△EK=0
解得:${v_B}=\sqrt{\frac{2gh}{3}}$
(2)设C球离开桌边的速度为vC
B球下落的过程中,B、C系统机械能守恒得:△EP=-mgh
动能:$△{E_K}=2×\frac{1}{2}mv_C^2-2×\frac{1}{2}mv_B^2$
由于△EP+△EK=0
所以${v_C}=\sqrt{\frac{5gh}{3}}$
答:(1)B球离开桌边的速度大小是$\sqrt{\frac{2gh}{3}}$
(2)C球离开桌边的速度大小是$\sqrt{\frac{5gh}{3}}$.
点评 本题在应用机械能守恒时应明确A落地后A即不能再分析,故应两次选择研究对象利用机械能守恒定律分析.


科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 三颗人造地球卫星A、B、C绕地球作匀速圆周运动,如图所示,已知mA=mB<mC,则三个卫星说法不正确的是( )
三颗人造地球卫星A、B、C绕地球作匀速圆周运动,如图所示,已知mA=mB<mC,则三个卫星说法不正确的是( )| A. | 线速度关系vA>vB=vC | |
| B. | 周期关系TA<TB=TC | |
| C. | 向心力大小FA=FB<FC | |
| D. | 半径与周期关系$\frac{{R}_{A}^{3}}{{T}_{A}^{2}}$=$\frac{{R}_{B}^{3}}{{T}_{B}^{2}}$=$\frac{{R}_{C}^{3}}{{T}_{C}^{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
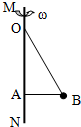 如图所示,在竖直转轴MN上距离为0.4m的O和A处分别用长0.5m和0.3m的细线连着一个质量为0.5kg的小球,使转轴通过细线带着小球转动起来.试求:
如图所示,在竖直转轴MN上距离为0.4m的O和A处分别用长0.5m和0.3m的细线连着一个质量为0.5kg的小球,使转轴通过细线带着小球转动起来.试求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,站在平板卡车上的人用水平力F推车,脚对车的静摩擦力向后为Ff,则下列说法中正确的是( )
如图所示,站在平板卡车上的人用水平力F推车,脚对车的静摩擦力向后为Ff,则下列说法中正确的是( )| A. | 当车匀速前进时,F和Ff对车做的功代数和为零 | |
| B. | 当车加速前进时,F和Ff对车做的功代数和为正值 | |
| C. | 当车减速前进时,F和Ff对车做的功代数和为正值 | |
| D. | 不管车如何运动,F和Ff对车做的功代数和均为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 (多选)第九届全国少数民族传统体育运动会于2011年9月10日在贵州省贵阳市举办.运动会上有一个骑射项目,如图所示,运动员骑在奔驰的马背上沿着跑道AB运动,拉弓放箭,射向他左侧的固定箭靶.假设运动员骑马奔驰的速度为v1,运动员静止时射出的箭的速度为v2,跑道离固定箭靶的最近距离为OA=d.若不计空气阻力的影响,要想命中靶心且射出的箭在空中飞行时间最短,则( )
(多选)第九届全国少数民族传统体育运动会于2011年9月10日在贵州省贵阳市举办.运动会上有一个骑射项目,如图所示,运动员骑在奔驰的马背上沿着跑道AB运动,拉弓放箭,射向他左侧的固定箭靶.假设运动员骑马奔驰的速度为v1,运动员静止时射出的箭的速度为v2,跑道离固定箭靶的最近距离为OA=d.若不计空气阻力的影响,要想命中靶心且射出的箭在空中飞行时间最短,则( )| A. | 运动员骑马奔驰时应该瞄准靶心放箭 | |
| B. | 运动员应该在离A点距离为$\frac{v_1}{v_2}d$的地方放箭 | |
| C. | 箭射到靶的最短时间为$\frac{d}{v_2}$ | |
| D. | 箭射到靶的最短时间为了$\frac{d}{{\sqrt{v_1^2+v_2^2}}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
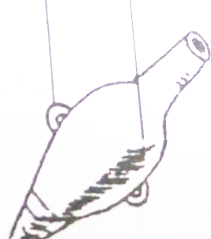 在对重力的本质还未认清之前,我国古代劳动人民就有了比较复杂的应用.我国西安半坡出土了一件距今约5000年的尖底陶器,如图所示,这种陶瓶口小腹大,有两耳在瓶腰偏下的地方,底尖,若用两根绳子系住两耳吊起瓶子,就能从井中取水,试分析人们是怎样利用尖底陶瓶在井中取水的.
在对重力的本质还未认清之前,我国古代劳动人民就有了比较复杂的应用.我国西安半坡出土了一件距今约5000年的尖底陶器,如图所示,这种陶瓶口小腹大,有两耳在瓶腰偏下的地方,底尖,若用两根绳子系住两耳吊起瓶子,就能从井中取水,试分析人们是怎样利用尖底陶瓶在井中取水的.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com