
分析 (1)根据万有引力提供向心力,结合卫星的轨道半径和周期求出月球的质量.
(2)根据万有引力等于重力,求出月球表面的重力加速度.
解答 解:(1)根据万有引力提供向心力有:$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$
解得:$M=\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{\;}^{2}}$
(2)月球表面上质量为m的物体:
$G\frac{Mm}{{R}_{\;}^{2}}=mg$
将月球质量M代入得:$g=\frac{GM}{{R}_{\;}^{2}}=\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{{R}_{\;}^{2}{T}_{\;}^{2}}$
答:(1)月球的质量M为$\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{\;}^{2}}$;
(2)月球表面的重力加速度g为$\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{{R}_{\;}^{2}{T}_{\;}^{2}}$.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.


科目:高中物理 来源: 题型:实验题
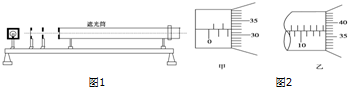
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 恒星的质量为$\frac{v^3}{2ωG}$ | B. | 行星运动的轨道半径为$\frac{v}{ω}$ | ||
| C. | 恒星的质量为$\frac{v^3}{ωG}$ | D. | 行星运动的加速度为vω |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{1}{2}$ma2t2 | B. | $\frac{1}{2}$mgat2 | C. | $\frac{1}{2}$m(g+a)at2 | D. | $\frac{1}{2}$mg2t2 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 在t1到t2时间内A、B两线圈相斥 | B. | 在t2到t3时间内A、B两线圈相斥 | ||
| C. | t1时刻两线圈间作用力最大 | D. | t2时刻两线圈间作用力最大 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
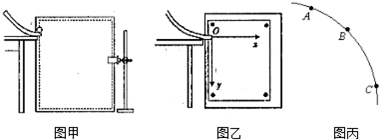
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 20 N | B. | 12 N | C. | 8 N | D. | 28 N |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
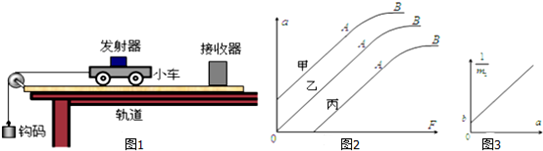
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com