
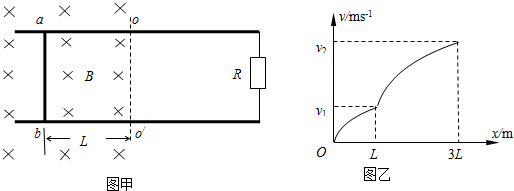
���� ��1�����ö��ܶ����ֱ��о�ab����λ��L��3L�Ĺ��̼�λ��ΪL���������̣���ʽ������Q1���Ƶ���������${F_��}=\frac{{{B^2}{L^2}{v_1}}}{R}$������ţ�ٵڶ���������ٶȣ�
��2�����ų���Bt=Bcos t���ɱ仯ʱ���պϻ�·�Ĵ�ͨ�����ı仯����Ϊ��=Bcos��t=BL2cos��t���綯�����ֵΪEm=B��L2�����Ÿ�Ӧǿ����B��С���㣬���ݽ���������صĴ�С��
���  �⣺��1��ab����λ��L��3L�Ĺ����У��ɶ��ܶ���
�⣺��1��ab����λ��L��3L�Ĺ����У��ɶ��ܶ���
F��3L-L��=$\frac{1}{2}m��v{\;}_2^2-v_1^2��$
ab���ڴų��з���L�����У�����F���Ĺ�����ab�����ӵĶ��ܺͻ�·�����ĵ���
FL=$\frac{1}{2}mv_1^2+{Q_1}$
����${Q_1}=\frac{m��v_2^2-3v_1^3��}{4}$
ab�����뿪�ų�ǰ˲�䣬ˮƽ�������ܰ�����F��������F���ã����ٶ�a����${F_��}=\frac{{{B^2}{L^2}{v_1}}}{R}$
����ţ�ٵڶ����ɵ� $a=\frac{{F-{F_��}}}{m}$
��á�$a=\frac{v_2^2-v_1^2}{4L}-\frac{{{B^2}{L^2}v}}{mR}$
��2�����ų���Bt=Bcos t���ɱ仯ʱ���պϻ�·�Ĵ�ͨ�����ı仯����Ϊ
��=Bcos��t=BL2cos��t
�ù����д�����Ȧ�Ĵ�ͨ��������Ȧ�ڴų����Խ��ٶȦ�����ת��������ͬ����˻�·�в��������磮
�綯�����ֵΪEm=B��L2����������������������
�ų���С���㣬�൱����Ȧת��90�㣬�����ķ�֮һ���ڣ�����
�в����ĵ���
Q2=${��\frac{E_m}{{\sqrt{2}}}��^2}\frac{1}{R}��\frac{T}{4}$
�� T=$\frac{2��}{��}$
������$��=\frac{{4{Q_2}R}}{{��{B^2}{L^4}}}$
��
��1���ڴ˹����е���R�ϲ����ĵ���Q1��$\frac{m��{v}_{2}^{2}-3{v}_{1}^{3}��}{4}$��ab�����뿪�ų�ǰ˲��ļ��ٶ�Ϊ$\frac{{v}_{2}^{2}-{v}_{1}^{2}}{4L}$-$\frac{{B}^{2}{L}^{2}v}{mR}$��
��2���صĴ�СΪ$\frac{4{Q}_{2}R}{��{B}^{2}{L}^{4}}$��
���� ����ؼ������ö��ܶ�����ţ�ٵڶ����ɡ��������ɵ���ѧ�͵�·�����о���Ÿ�Ӧ���������ҽ��������Ҫ����Чֵ������ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
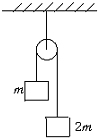 �����������ֱ�Ϊm��2m�����ֵ�������Ħ�������ƣ���ʼʱ������ס2m�����壬�ͷź�2m������Ӿ�ֹ��ʼ�½�h����ٶ��Ƕ��٣�������
�����������ֱ�Ϊm��2m�����ֵ�������Ħ�������ƣ���ʼʱ������ס2m�����壬�ͷź�2m������Ӿ�ֹ��ʼ�½�h����ٶ��Ƕ��٣�������| A�� | $\sqrt{\frac{2gh}{3}}$ | B�� | $\sqrt{\frac{1gh}{3}}$ | C�� | $\sqrt{\frac{2gh}{5}}$ | D�� | $\sqrt{2gh}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
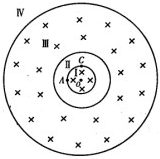 ��ͼ��ʾ�������뾶�ֱ�ΪR��2R��6R��ͬ��Բ���ռ��Ϊ���ĸ���������Բ�������ͻ�����������д�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȷֱ�ΪB��$\frac{B}{2}$��һ�����Ӵ������߽��ϵ�A�����ٶ�v�ذ뾶��������ų������ų�ƫתǡ�ô������߽��ϵ�C��ɳ���AO��ֱCO����������ӵ��˶�������˵����ȷ���ǣ�������
��ͼ��ʾ�������뾶�ֱ�ΪR��2R��6R��ͬ��Բ���ռ��Ϊ���ĸ���������Բ�������ͻ�����������д�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȷֱ�ΪB��$\frac{B}{2}$��һ�����Ӵ������߽��ϵ�A�����ٶ�v�ذ뾶��������ų������ų�ƫתǡ�ô������߽��ϵ�C��ɳ���AO��ֱCO����������ӵ��˶�������˵����ȷ���ǣ�������| A�� | �������ս��뿪�����������������˶� | |
| B�� | �������ս�һֱ���������������Բ���˶� | |
| C�� | �����ܹ��ص���ʼ��A�����ܶ���ʼ���˶� | |
| D�� | �����ܹ��ص���ʼ��A���һص���ʼ��ǰ������������˶���ʱ��������������˶�ʱ���6�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
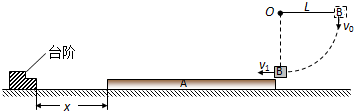
 ��ͼ��ʾ���ᵯ�ɵ�һ�˹̶�����һ���뻬��B������B��ֹ��ˮƽ�����ϣ����ɴ���ԭ��״̬������A�Ӱ뾶ΪR�Ĺ⻬$\frac{1}{4}$Բ�������ٻ��£���P�㻬��ˮƽ���죬��A��������s1=Rʱ����B��������ײʱ�伫�̣�����A��B������һ���˶���������ճ�������Aǡ�÷��س�����P��ֹͣ����A��Bѹ�����ɹ���ʼ��δ�������ɵĵ����ȣ���֪����A��B������ͬ��A��B����Ϊ�ʵ㣩�����뵼��Ļ���Ħ��������Ϊ��=0.1���������ٶ�Ϊg������
��ͼ��ʾ���ᵯ�ɵ�һ�˹̶�����һ���뻬��B������B��ֹ��ˮƽ�����ϣ����ɴ���ԭ��״̬������A�Ӱ뾶ΪR�Ĺ⻬$\frac{1}{4}$Բ�������ٻ��£���P�㻬��ˮƽ���죬��A��������s1=Rʱ����B��������ײʱ�伫�̣�����A��B������һ���˶���������ճ�������Aǡ�÷��س�����P��ֹͣ����A��Bѹ�����ɹ���ʼ��δ�������ɵĵ����ȣ���֪����A��B������ͬ��A��B����Ϊ�ʵ㣩�����뵼��Ļ���Ħ��������Ϊ��=0.1���������ٶ�Ϊg�������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
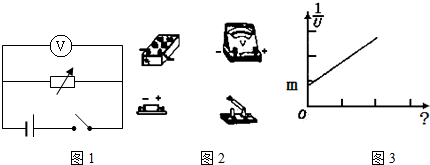
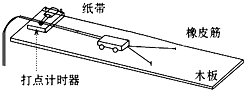 ̽������ԭ����ֹ���������Ĺ��������õ��ٶȵĹ�ϵʱ��ʵ��װ����ͼ��ʾ��ʵ����Ҫ�������£�
̽������ԭ����ֹ���������Ĺ��������õ��ٶȵĹ�ϵʱ��ʵ��װ����ͼ��ʾ��ʵ����Ҫ�������£��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com