
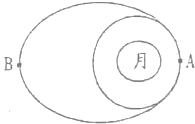
 ���϶�һ�š��ijɹ����䣬Ϊʵ���л����弸ǧ��ı���������������Ҫ��һ������ͼ��ʾ�����϶�һ�š��Ƚ������·��е���Բ�����Ȼ������Բ������µ�A���������·���Բ�������֪���϶�һ�š����·��е���Բ���Զ�µ�B���������߶�ΪH������֪���϶�һ�š�����Բ�������ʱ�����������ĸ߶�Ϊh����������ΪT������İ뾶ΪR��������������ΪG����Ȼ��������ڷɴ��ϣ��ٿطɴ���������渽����ֱƽ���ڸ��壬����͵㸽�����뾶Ϊr��Բ���˶����Ա������m���ɴ�������͵�ʱ���ٶ���v����
���϶�һ�š��ijɹ����䣬Ϊʵ���л����弸ǧ��ı���������������Ҫ��һ������ͼ��ʾ�����϶�һ�š��Ƚ������·��е���Բ�����Ȼ������Բ������µ�A���������·���Բ�������֪���϶�һ�š����·��е���Բ���Զ�µ�B���������߶�ΪH������֪���϶�һ�š�����Բ�������ʱ�����������ĸ߶�Ϊh����������ΪT������İ뾶ΪR��������������ΪG����Ȼ��������ڷɴ��ϣ��ٿطɴ���������渽����ֱƽ���ڸ��壬����͵㸽�����뾶Ϊr��Բ���˶����Ա������m���ɴ�������͵�ʱ���ٶ���v�������� ��1���϶�һ��������������Բ���˶������������ṩ����������ţ�ٵڶ�����������������ʽ��������������
��2��Ӧ������������ʽ��ţ�ٵڶ����ɷ������⣮
��3��Ӧ������������ʽ��ţ�ٵڶ�����������ζ��Ա����������
��� �⣺��1�����������ṩ����������ţ�ٵڶ����ɵã�
G$\frac{Mm}{��R+h��^{2}}$=m$��\frac{2��}{T}��^{2}$��R+h����������������M=$\frac{4{��}^{2}��R+h��^{3}}{G{T}^{2}}$��
��2����ţ�ٵڶ����ɵã�G$\frac{Mm}{��R+H��^{2}}$=ma����ã�a=$\frac{4{��}^{2}��R+h��^{3}}{��R+H��^{2}{T}^{2}}$��
���϶�һ�š������·��е���Բ������µ�Aʱ��������Բ�����
����뾶��С���ɴ�Ҫ�������˶����ɴ���Ҫ���٣��ɴ�Ӧ���������
��3�����Ա����ţ�ٵڶ����ɵã�F-G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{r}$��
����������F=$\frac{{4��}^{2}m��R+h��^{3}}{{R}^{2}{T}^{2}}$+$\frac{m{v}^{2}}{r}$��
�𣺣�1�����������M��$\frac{4{��}^{2}��R+h��^{3}}{G{T}^{2}}$��
��2�����϶�һ�š������·��е���Բ���Զ�µ�Bʱ�ļ��ٶ�Ϊ$\frac{4{��}^{2}��R+h��^{3}}{��R+H��^{2}{T}^{2}}$���ɴ�Ӧ�����������
��3���ٿطɴ���������渽����ֱƽ���ڸ��徭����͵㣬��λ���Ա��������F�ǣ�$\frac{{4��}^{2}m��R+h��^{3}}{{R}^{2}{T}^{2}}$+$\frac{m{v}^{2}}{r}$��
���� ���⿼���������������ɵ�Ӧ�ã�֪�����������ṩ����������ȷ����Ĺؼ���Ӧ������������ʽ��ţ�ٵڶ����ɿ��Խ��⣬�����dz����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ��һ�����˺�һ��С���ò�ͬ��ѩ�������Ϊ�ȵ���бѩ���ϻ�ѩ�����˺�С�������˺�ѩ���������ϴ�֮����һ����ˣ�����б��ƽ�У���������������ǡ�������»��������ˡ�С��ͬʱ�ɿ���ˣ�����ܵ�����ǣ�������
��ͼ��ʾ��һ�����˺�һ��С���ò�ͬ��ѩ�������Ϊ�ȵ���бѩ���ϻ�ѩ�����˺�С�������˺�ѩ���������ϴ�֮����һ����ˣ�����б��ƽ�У���������������ǡ�������»��������ˡ�С��ͬʱ�ɿ���ˣ�����ܵ�����ǣ�������| A�� | ���˼����»���С�������»��������ٶȴ�С��ͬ | |
| B�� | ���˼����»���С�������»��������ٶȴ�С��ͬ | |
| C�� | ���˼����»���С�������»��������ٶȴ�С��ͬ | |
| D�� | ���˶������»��������ٶȲ�ͬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ͼ����ʾ��ƽ�а������������Ϊd���������ӵ�ѹ��ʱ��仯ͼ����ͼ����ʾ��t=0ʱ�̣�����Ϊm��������Ϊq��������ƽ���ڼ�����ٶ�V0�����������t1=3Tʱ��ǡ�ô��¼����Ե������������������ӵ��������ƣ���
ͼ����ʾ��ƽ�а������������Ϊd���������ӵ�ѹ��ʱ��仯ͼ����ͼ����ʾ��t=0ʱ�̣�����Ϊm��������Ϊq��������ƽ���ڼ�����ٶ�V0�����������t1=3Tʱ��ǡ�ô��¼����Ե������������������ӵ��������ƣ����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
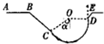 ���弫���˶�������ͼ��ʾ������ABˮƽ����s=5m��BC��б��CDΪ��ֱƽ���ڰ뾶R=1.0m�Ĺ⻬�ػ������Բ��O��C����������ֱ����ļнǦ�=53�㣬D�����߷�����ֱ��һ������m=60kg���������壩�˶�Ա��A���ɾ�ֹ��������B��ɳ���ǡ�ô�C������߷������Բ�λ������ٴ�D����ֱ�����˶�������ߵ�E����֪E�����Բ��������͵�ĸ߶�H=2.2m����֪�������ٶ�g=10m/s2��sin53��=0.8��cos53��=0.6���������������ƣ�
���弫���˶�������ͼ��ʾ������ABˮƽ����s=5m��BC��б��CDΪ��ֱƽ���ڰ뾶R=1.0m�Ĺ⻬�ػ������Բ��O��C����������ֱ����ļнǦ�=53�㣬D�����߷�����ֱ��һ������m=60kg���������壩�˶�Ա��A���ɾ�ֹ��������B��ɳ���ǡ�ô�C������߷������Բ�λ������ٴ�D����ֱ�����˶�������ߵ�E����֪E�����Բ��������͵�ĸ߶�H=2.2m����֪�������ٶ�g=10m/s2��sin53��=0.8��cos53��=0.6���������������ƣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���Ŵֲڵ�б���ȼ����»������� | |
| B�� | �Ӽ���Ա��ϸ��ǣ�ŵ�����ֱƽ������Բ���˶��ġ�С���ǡ������ƿ��������� | |
| C�� | ��������ֱ������������С�� | |
| D�� | �Ƶ���������Բ����˶�������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
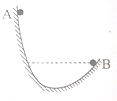 ��ͼ��ʾ��һ������ٶ�v1��������A�㴦�»����˶���B�㴦�ٶȴ�С��Ϊv1����������ٶ�v2��v2��v1���Դ�A���»������˶���B��ʱ�ٶȵĴ�С����������
��ͼ��ʾ��һ������ٶ�v1��������A�㴦�»����˶���B�㴦�ٶȴ�С��Ϊv1����������ٶ�v2��v2��v1���Դ�A���»������˶���B��ʱ�ٶȵĴ�С����������| A�� | �Դ���v2 | B�� | ��С��v2 | C�� | ����v2 | D�� | ��С��v1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
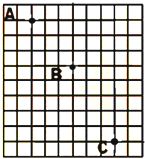 ͼΪһС����ƽ���˶���������Ƭ��һ���֣�ͼ�б�������ı߳���Ϊ5���ף����ȡ�������ٶ�g=10m/s2����ô��
ͼΪһС����ƽ���˶���������Ƭ��һ���֣�ͼ�б�������ı߳���Ϊ5���ף����ȡ�������ٶ�g=10m/s2����ô���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | Ek2��Ek1=4��1 | B�� | Ek2��Ek1=3��1 | C�� | E2��E1=2��1 | D�� | E2��E1=1��1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
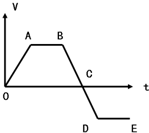
| A�� | ��AB�Σ��ʵ㾲ֹ | |
| B�� | ��BD�Σ��ʵ����ȼ���ֱ���˶� | |
| C�� | ��0ABCDE���������У��ʵ����ȱ���ֱ���˶� | |
| D�� | ��0A��CD�Σ��ʵ㶼���ȼ���ֱ���˶� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com