
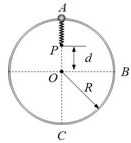
 如图,在竖直平面内固定一半径为R的光滑细圆环,质量为m的小球套在细圆环,劲度系数k=$\frac{mg}{R}$的轻质弹簧一端固定在P点另一端与小球相连,P位于圆心O的正上方且距离d=$\frac{1}{2}$R,B与O在同一水平线上.已知该弹簧原长L0<<R,弹簧的弹性势能可表示为E=$\frac{1}{2}$kx2(x为形变量),重力加速度为g,当小球在圆环顶点A从静止开始经过B下滑到最低点C,求:
如图,在竖直平面内固定一半径为R的光滑细圆环,质量为m的小球套在细圆环,劲度系数k=$\frac{mg}{R}$的轻质弹簧一端固定在P点另一端与小球相连,P位于圆心O的正上方且距离d=$\frac{1}{2}$R,B与O在同一水平线上.已知该弹簧原长L0<<R,弹簧的弹性势能可表示为E=$\frac{1}{2}$kx2(x为形变量),重力加速度为g,当小球在圆环顶点A从静止开始经过B下滑到最低点C,求:分析 (1)根据小球与弹簧组成的系统机械能守恒,求小球经过C点时的速度vc.
(2)由牛顿第二定律求小球经过C点时,圆环对小球的作用力大小及方向,再由牛顿第三定律得到小球经过C点对圆环的作用力大小及方向.
(3)结合上题的表达式,分析d的值.
解答 解:(1)在A位置,弹簧的弹性势能为 Ep1=$\frac{1}{2}k({L}_{0}-\frac{R}{2})^{2}$
在C位置,弹簧的弹性势能为 Ep2=$\frac{1}{2}k(2R-{L}_{0})^{2}$
根据小球与弹簧组成的系统机械能守恒得:
2mgR+Ep1=Ep2+$\frac{1}{2}m{v}_{C}^{2}$
解得 vC=$\sqrt{\frac{gR}{4}+3g{L}_{0}}$
(2)在C点,设圆环对小球的作用力大小为F,方向向下,由牛顿第二定律得:
k(2R-L0)-mg-F=m$\frac{{v}_{C}^{2}}{R}$
解得 F=$\frac{3}{4}$mg-$\frac{7mg{L}_{0}}{4R}$
根据牛顿第三定律得,小球经过C点对圆环的作用力大小为$\frac{3}{4}$mg-$\frac{7mg{L}_{0}}{4R}$,方向向上.
(3)小球经过C点时对圆环的作用力为零时,在C点,由牛顿第二定律有:
k(2R-L0)-mg=m$\frac{{v}_{C}^{2}}{R}$
根据小球与弹簧组成的系统机械能守恒得:
2mgR+$\frac{1}{2}k(R-d-{L}_{0})^{2}$=$\frac{1}{2}k(2R-{L}_{0})^{2}$+$\frac{1}{2}m{v}_{C}^{2}$
联立解得 d=R-L0-$\sqrt{6{R}^{2}-5R{L}_{0}+{L}_{0}^{2}-\frac{5mgR}{k}}$
答:(1)小球经过C点时的速度vc是$\sqrt{\frac{gR}{4}+3g{L}_{0}}$.
(2)小球经过C点对圆环的作用力大小$\frac{3}{4}$mg-$\frac{7mg{L}_{0}}{4R}$,方向向上;
(3)为使小球经过C点时对圆环的作用力为零,P、O间的距离d应为R-L0-$\sqrt{6{R}^{2}-5R{L}_{0}+{L}_{0}^{2}-\frac{5mgR}{k}}$.
点评 此题中要注意小球的机械能不守恒,球和弹簧组成的系统机械能才守恒.要正确分析圆周运动向心力的来源,由牛顿第二定律和机械能守恒定律结合研究.


科目:高中物理 来源: 题型:选择题
| A. | 在电场中某点的电势为零,则该点的电场强度一定为零 | |
| B. | 电场中某点的场强大小等于单位电量的试探电荷在该点所受的电场力大小 | |
| C. | 根据公式U=Ed 知,在匀强电场中两点间的距离越大,电势差就越大 | |
| D. | 电荷沿电场线方向移动时,电势能一定增加 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 在相互垂直的匀强电场和匀强磁场中,有一倾角为θ,足够长的光滑绝缘斜面,磁感应强度为B,方向垂直纸面向外,电场方向竖直向上,有一质量为m,带电量为+q的小球静止在斜面顶端,这时小球对斜面的正压力恰好为零,如图所示,若迅速把电场方向反转竖直向下,则( )
在相互垂直的匀强电场和匀强磁场中,有一倾角为θ,足够长的光滑绝缘斜面,磁感应强度为B,方向垂直纸面向外,电场方向竖直向上,有一质量为m,带电量为+q的小球静止在斜面顶端,这时小球对斜面的正压力恰好为零,如图所示,若迅速把电场方向反转竖直向下,则( )| A. | 小球能在斜面上连续滑行距离x=$\frac{{m}^{2}gco{s}^{2}θ}{{q}^{2}{B}^{2}sinθ}$ | |
| B. | 小球能在斜面上连续滑行距离x=$\frac{{m}^{2}gco{s}^{2}θ}{{4q}^{2}{B}^{2}sinθ}$ | |
| C. | C、小球能在斜面上连续滑行的时间t=$\frac{mcotθ}{qB}$ | |
| D. | 小球不会离开斜面 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
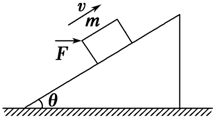 如图所示,一个质量为m的物块放在倾角为θ=37°的固定斜面上,物块与斜面的动摩擦因数为0.2,现对物块施加一个水平向右的作用力,使物块沿斜面匀速运动.(sin37°=0.6,cos37°=0.8计算结果可用分数表示)
如图所示,一个质量为m的物块放在倾角为θ=37°的固定斜面上,物块与斜面的动摩擦因数为0.2,现对物块施加一个水平向右的作用力,使物块沿斜面匀速运动.(sin37°=0.6,cos37°=0.8计算结果可用分数表示)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
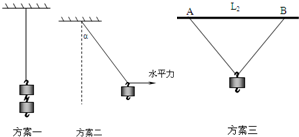
 如图所示,A、B两球的质量均为m,固定在轻质弹簧的两端,分别用细绳悬于O点,其中A球处在光滑竖直墙面和光滑水平地面的交界处,已知两球均处于平衡状态,OAB恰好构成一个等边三角形,重力加速度为g,则下列说法正确的是 ( )
如图所示,A、B两球的质量均为m,固定在轻质弹簧的两端,分别用细绳悬于O点,其中A球处在光滑竖直墙面和光滑水平地面的交界处,已知两球均处于平衡状态,OAB恰好构成一个等边三角形,重力加速度为g,则下列说法正确的是 ( )| A. | 球A可能受到五个力的作用 | B. | 弹簧对球A的弹力大于对球B的弹力 | ||
| C. | 绳OB对球B的拉力大小一定等于mg | D. | 绳OA对球A的拉力大小大于1.5mg |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,光滑水平面上,小球m在拉力F作用下做匀速圆周运动,若小球运动到P点时,拉力F发生变化,下列说法中正确的是( )
如图所示,光滑水平面上,小球m在拉力F作用下做匀速圆周运动,若小球运动到P点时,拉力F发生变化,下列说法中正确的是( )| A. | 若拉力突然消失,小球将沿轨迹Pa做直线运动 | |
| B. | 若拉力突然变小,小球将沿轨迹Pc做近心运动 | |
| C. | 若拉力突然变大,小球将沿轨迹Pb做离心运动 | |
| D. | 无论拉力如何变化,小球均沿原轨迹做圆周运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com