
 如图所示,一长为L=18m的传送带水平放置,可以看成质点的物块静止于传送带的左端,物块与传送带之间的动摩擦因数为μ=0.2.(g=10m/s2)
如图所示,一长为L=18m的传送带水平放置,可以看成质点的物块静止于传送带的左端,物块与传送带之间的动摩擦因数为μ=0.2.(g=10m/s2)
 a1t12=
a1t12=
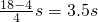
 物块速度为v,
物块速度为v,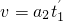

 离开传送带,
离开传送带,
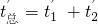
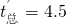 s
s

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中物理 来源: 题型:
 如图所示,一长为L的轻绳,一端固定在天花板上,另一端系一质量为m的小球,球绕竖直轴线O1O2做匀速圆周运动,绳与竖直轴线间的夹角为θ,则下述说法中正确的是( )
如图所示,一长为L的轻绳,一端固定在天花板上,另一端系一质量为m的小球,球绕竖直轴线O1O2做匀速圆周运动,绳与竖直轴线间的夹角为θ,则下述说法中正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,一长为L的细线,上端固定,下端栓一质量为m、带电量为q的带正电小球,处于水平向右的匀强电场中.已知小球在B点静止时细线与水平方向夹角为60°.现将细线与小球拉到与O点在同一水平面上的A点,然后由静止释放小球,重力加速度为g
如图所示,一长为L的细线,上端固定,下端栓一质量为m、带电量为q的带正电小球,处于水平向右的匀强电场中.已知小球在B点静止时细线与水平方向夹角为60°.现将细线与小球拉到与O点在同一水平面上的A点,然后由静止释放小球,重力加速度为g查看答案和解析>>
科目:高中物理 来源: 题型:
 (2007?苏州二模)如图所示,一长为L的薄壁玻璃管放置在水平面上,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带负电,电荷量为q、质量为m.玻璃管右边的空间存在方向竖直向上、磁感应强度为B的匀强磁场.磁场的左边界与玻璃管平行,右边界足够远.玻璃管和小球一起以水平速度v0垂直于左边界向右运动,由于外力的作用,玻璃管进入磁场后速度保持不变,经一段时间后小球从玻璃管凸端滑出.设运动过程中小球的电荷量保持不变,不计一切摩擦.求
(2007?苏州二模)如图所示,一长为L的薄壁玻璃管放置在水平面上,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带负电,电荷量为q、质量为m.玻璃管右边的空间存在方向竖直向上、磁感应强度为B的匀强磁场.磁场的左边界与玻璃管平行,右边界足够远.玻璃管和小球一起以水平速度v0垂直于左边界向右运动,由于外力的作用,玻璃管进入磁场后速度保持不变,经一段时间后小球从玻璃管凸端滑出.设运动过程中小球的电荷量保持不变,不计一切摩擦.求查看答案和解析>>
科目:高中物理 来源: 题型:
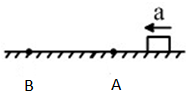 如图所示,一长为l的长方形木块在水平面上以加速度a做匀加速直线运动.A、B之间有一定的距离,木块前端P先到达A点,之后经过t1时间整个木块通过了A点,而前端P到达B点后,整个木块通过B点所用时间为t2.求:
如图所示,一长为l的长方形木块在水平面上以加速度a做匀加速直线运动.A、B之间有一定的距离,木块前端P先到达A点,之后经过t1时间整个木块通过了A点,而前端P到达B点后,整个木块通过B点所用时间为t2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
 (2010?南昌一模)如图所示,一长为L、质量为m的柔软匀质物体从光滑的水平面上以初速度v0向右滑上同一水平的台面,物体前端在台面上滑动S距离停下来.物体与台面间的动摩擦因数为μ而且S>L,则物体的初速度v0为( )
(2010?南昌一模)如图所示,一长为L、质量为m的柔软匀质物体从光滑的水平面上以初速度v0向右滑上同一水平的台面,物体前端在台面上滑动S距离停下来.物体与台面间的动摩擦因数为μ而且S>L,则物体的初速度v0为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com