
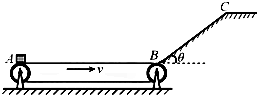
 用如图所示的浅色水平传送带AB和斜面BC将货物运送到斜面的顶端.AB距离L=11m,传送带始终以v=12m/s匀速顺时针运行.传送带B端靠近倾角θ=37°的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔t=1.0s将一个质量m=10kg、底部有碳粉的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的$\frac{1}{11}$,不计传送带轮的大小,g=10m/s2(sin37°=0.6,cos37°=0.8).求:
用如图所示的浅色水平传送带AB和斜面BC将货物运送到斜面的顶端.AB距离L=11m,传送带始终以v=12m/s匀速顺时针运行.传送带B端靠近倾角θ=37°的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔t=1.0s将一个质量m=10kg、底部有碳粉的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的$\frac{1}{11}$,不计传送带轮的大小,g=10m/s2(sin37°=0.6,cos37°=0.8).求:分析 (1)货物箱在传送带上做匀加速运动过程,根据牛顿第二定律求出加速度,由速度位移关系公式求出货物箱运动到传送带右端时的速度大小,根据货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的,得到货物箱刚冲上斜面时的速度.货物箱在斜面上向上运动过程中做匀减速运动,已知初速度、末速度为零,位移为s,由速度位移关系公式求出加速度大小,由牛顿第二定律求出斜面与货物箱之间的动摩擦因数μ.
(2)由运动学公式分别求出货物箱由A运动到B的时间和由B运动到C的时间,得到第一个货物箱冲上斜面C端时第二个货物箱刚好冲上斜面,然后货物箱沿斜面向下做匀加速运动,
由牛顿第二定律求出加速度,当第一个货物箱与第二个货物箱相遇时,两者位移大小之和等于斜面的长度s,由位移公式求出相遇时间,再求出两个货物箱在斜面上相遇的位置到C端的距离.
(3)根据位移公式求出第1s内货箱和传送带运动的位移,进而得出货箱第1s留下的痕迹,同理,再求出第2s内第一个货箱留下的痕迹,从而知道第一、二两个货箱由1m重合,t0=2s时,第二个货箱在传送带上运动了1s,留下的痕迹与第一个货箱留下的痕迹相等,最后求出2s内货物箱在传送带上留下的痕迹的总长度.
解答 解:(1)货物箱在传送带上做匀加速运动过程,根据牛顿第二定律有:μ0mg=ma1
解得:a1=μ0g=0.55×10=5.5m/s2
到传送带右端的速度为:${v}_{1}=\sqrt{2{a}_{1}L}$=$\sqrt{2×5.5×11}$m/s=11m/s,
v1<v=12m/s,说明货物箱在传送带上一直做匀加速运动,
运动至斜面底端的速度为:${v}_{2}={v}_{1}-\frac{1}{11}{v}_{1}=\frac{10}{11}{v}_{1}=\frac{10}{11}×11m/s$=10m/s,
货箱在斜面上滑过程有:${a}_{2}=μgcosθ+gsinθ=\frac{{{v}_{2}}^{2}}{2s}$,
代入数据解得:μ=0.5.
(2)货箱沿斜面上滑过程有:a2=μgcosθ+gsinθ=0.5×10×0.8+10×0.6m/s2=10m/s2,
t1=1s,第二个货物箱在斜面B端时与第一个货物箱刚好从C端下滑,
货箱沿斜面下滑过程,根据牛顿第二定律有:a3=gsinθ-μgcosθ=6-4m/s2=2m/s2•
设第一个货物箱在斜面C端沿斜面向下运动与第二个货物箱相撞的过程所用时间为t2,有:
$s={v}_{2}{t}_{2}-\frac{1}{2}{a}_{2}{{t}_{2}}^{2}+\frac{1}{2}{a}_{3}{{t}_{2}}^{2}$,
解得:${t}_{2}=\frac{5-\sqrt{5}}{4}s$,
两个货物箱在斜面上相遇的位置到C端的距离:d=$\frac{1}{2}{a}_{3}{{t}_{2}}^{2}=\frac{15-5\sqrt{5}}{8}m$.
(3)第1s内,货箱的位移:${x}_{1}=\frac{1}{2}{a}_{1}{t}^{2}=\frac{1}{2}×5.5×1m=2.75m$,
传送带的位移:x2=vt=12×1m=12m,
第1s留下的痕迹:d1=x2-x1=12-2.75m=9.25m.
则t=1s时,第二个货箱轻放在第一个货物后2.75m处,第一个货箱前9.25m有痕迹
第2s内,对第一个货箱:v0=a1t=5.5×1m/s=5.5m/s,
${x}_{1}′={v}_{0}t+\frac{1}{2}{a}_{1}{t}^{2}$=$5.5×1+\frac{1}{2}×5.5×1$m=8.25m,
第一个货箱留下的痕迹:d2=x2-x1′=12-8.25m=3.75m,
可知一二两个货箱的痕迹有1m重合,
t0=2s时,第二个货箱在传送带上运动了1s,留下的痕迹:d3=d1=9.25m,
则2s内,货箱留下的痕迹总长度为:△s=d1+d2+d3-1m=21.25m.
答:(1)斜面与货物箱之间的动摩擦因数为0.5;
(2)两个货物箱在斜面上相撞的位置到C点的距离为$\frac{15-5\sqrt{5}}{8}m$;
(3)货物箱在传送带上留下的痕迹长度为21.25m.
点评 此题文字较多,首先要有耐心读题,该题涉及到相对运动的过程,要认真分析物体的受力情况和运动情况,对于传送带问题,关键是分析物体的运动情况,要边计算边分析,不能只定性分析.


科目:高中物理 来源: 题型:选择题
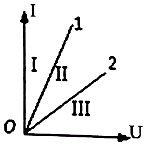 如图所示,是两只定值电阻R1、R2的I-U图象.有关R1、R2的大小,及它们串联或并联后的I-U图象所在区域,下列判断正确的是( )
如图所示,是两只定值电阻R1、R2的I-U图象.有关R1、R2的大小,及它们串联或并联后的I-U图象所在区域,下列判断正确的是( )| A. | R1>R2,并联后在区域III | B. | R1>R2.并联后在区域II | ||
| C. | R1<R2,串联后在区域III | D. | R1<R2,串联后在区域I |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 两个完全相同的条形磁铁放在平板AB上,磁铁的N、S极如图所示.开始时平板及磁铁均处于水平位置上,且静止不动.
两个完全相同的条形磁铁放在平板AB上,磁铁的N、S极如图所示.开始时平板及磁铁均处于水平位置上,且静止不动.| A. | 开始时两磁铁静止不动,说明磁铁间的作用力是排斥力 | |
| B. | 开始时两磁铁静止不动,说明磁铁间的吸引力小于静摩擦力 | |
| C. | 第(1)过程中磁铁开始滑动时,平板正在向上加速 | |
| D. | 第(2)过程中磁铁开始滑动时,平板正在向下加速 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | F1>F2 | B. | L1>L2 | C. | x1<x2 | D. | a1<a2 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
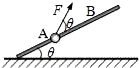 如图,一质量m=2kg的小球套在一根固定的足够长的直杆上,直杆与水平面夹角θ=37°.现小球在与杆也成θ角的斜向上F=20N的外力作用下,从A点静止出发向上运动.已知杆与球间的动摩擦因数μ=0.5,g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图,一质量m=2kg的小球套在一根固定的足够长的直杆上,直杆与水平面夹角θ=37°.现小球在与杆也成θ角的斜向上F=20N的外力作用下,从A点静止出发向上运动.已知杆与球间的动摩擦因数μ=0.5,g取10m/s2,sin37°=0.6,cos37°=0.8.求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
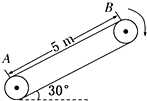 如图所示,传送带与水平面之间的夹角为θ=30°,其上A、B两点间的距离为L=5m,传送带在电动机的带动下以v=1m/s的速度匀速运动,现将一质量为m=5kg的小物体(可视为质点)轻放在传送带的A点,已知小物体与传送带之间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,在传送带将小物体从A点传送到B点的过程中,求:(g取10m/s2)
如图所示,传送带与水平面之间的夹角为θ=30°,其上A、B两点间的距离为L=5m,传送带在电动机的带动下以v=1m/s的速度匀速运动,现将一质量为m=5kg的小物体(可视为质点)轻放在传送带的A点,已知小物体与传送带之间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,在传送带将小物体从A点传送到B点的过程中,求:(g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:填空题
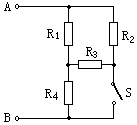 如图所示,R1=R2=R3=3Ω,R4=6Ω,UAB=12V,当S断开时,通过R1的电流为1A;当S闭合后,通过R1的电流为2.4A;R3消耗的功率为7.68W.
如图所示,R1=R2=R3=3Ω,R4=6Ω,UAB=12V,当S断开时,通过R1的电流为1A;当S闭合后,通过R1的电流为2.4A;R3消耗的功率为7.68W.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com