
分析 根据某时刻A、B两质点振动正好经过平衡位置及A、B之间有两个波峰,可以画出A、B间可能的波形,由图可求出波长λ.再根据t时间内质点B由平衡位置恰好到达波峰位置,又可求出质点振动的周期T.由公式v=$\frac{λ}{T}$就可以求出这列波的波速v.
解答 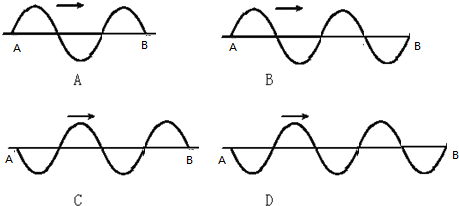 解:据题根据下列四种情况求解:
解:据题根据下列四种情况求解:
如图A所示,波长为 λA=$\frac{2}{3}$d,由 t=(n+$\frac{1}{4}$)TA,(n=0,1,2…),周期为 TA=$\frac{4t}{4n+1}$,波速为 v=$\frac{{λ}_{A}}{{T}_{A}}$=$\frac{(4n+1)d}{6t}$
如图B所示,波长为 λB=$\frac{1}{2}$d,t=(n+$\frac{3}{4}$)TB,(n=0,1,2…),
周期为 TB=$\frac{4t}{4n+3}$,波速为 v=$\frac{{λ}_{B}}{{T}_{B}}$=$\frac{(4n+3)d}{8t}$
如图C所示,波长为 λC=$\frac{1}{2}$d,t=(n+$\frac{1}{4}$)TC,(n=0,1,2…),
周期为 TC=$\frac{4t}{4n+1}$,波速为 v=$\frac{{λ}_{C}}{{T}_{C}}$=$\frac{(4n+1)d}{8t}$
如图D所示,波长为 λD=$\frac{4}{5}$d,t=(n+$\frac{3}{4}$)TD,(n=0,1,2…),
周期为 TD=$\frac{4t}{4n+3}$,波速为 v=$\frac{{λ}_{D}}{{T}_{D}}$=$\frac{(4n+3)d}{5t}$
答:波速可能为$\frac{(4n+1)d}{6t}$,$\frac{(4n+3)d}{8t}$,$\frac{(4n+1)d}{8t}$,$\frac{(4n+3)d}{5t}$,(n=0,1,2…).
点评 解决本题的关键确定出M、N间只有两个波峰的可能情况,结合波速、波长、周期的关系,运用波的周期性进行求解.


科目:高中物理 来源: 题型:选择题
| A. | 2s末A点的振动速度大于B点的振动速度 | |
| B. | 1s末A、B两质点的位移相同 | |
| C. | 波长为12m | |
| D. | 波速一定为1m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 核能是一种常规能源 | |
| B. | 煤、石油、天然气都是常规能源 | |
| C. | 大量消耗常规能源加剧了“温室效应” | |
| D. | 燃烧煤炭时产生的二氧化硫使雨水酸度升高,形成酸雨 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 飞机做的是匀速直线运动 | |
| B. | 飞机上的乘客对座椅的压力略大于地球对乘客的引力 | |
| C. | 飞机上的乘客对座椅的压力略小于地球对乘客的引力 | |
| D. | 飞机上的乘客对座椅的压力为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成一个圆锥摆,当细线与竖直线的夹角为θ时,求:
如图所示,将一质量为m的摆球用长为L的细绳吊起,上端固定,使摆球在水平面内做匀速圆周运动,细绳就会沿圆锥面旋转,这样就构成一个圆锥摆,当细线与竖直线的夹角为θ时,求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
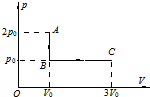 图为一定质量理想气体的压强P与体积V的关系图象,它由状态A经等容过程到状态B,再经过等压过程到状态C.设A、B、C状态对应的温度分别为TA、TB、TC,则TA=$\frac{2}{3}$TC,从状态B到状态C过程气体吸热(填“吸”、“放”)
图为一定质量理想气体的压强P与体积V的关系图象,它由状态A经等容过程到状态B,再经过等压过程到状态C.设A、B、C状态对应的温度分别为TA、TB、TC,则TA=$\frac{2}{3}$TC,从状态B到状态C过程气体吸热(填“吸”、“放”)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
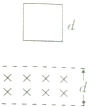 如图,竖直平面(纸面)两水平线间存在宽度为d的匀强磁场,磁场方向垂直纸面向里.一质量为m、边长也为d的正方形线圈从磁场上方某处自由落下,t1时刻线圈的下边进入磁场,t2时刻线圈的上边进入磁场,t3时刻线圈上边离开磁场.已知线圈平面在下落过程中始终与磁场方向垂直,且线圈上、下边始终与磁场边界平行,不计空气阻力,则线圈下落过程中的v-t图象可能正确的是( )
如图,竖直平面(纸面)两水平线间存在宽度为d的匀强磁场,磁场方向垂直纸面向里.一质量为m、边长也为d的正方形线圈从磁场上方某处自由落下,t1时刻线圈的下边进入磁场,t2时刻线圈的上边进入磁场,t3时刻线圈上边离开磁场.已知线圈平面在下落过程中始终与磁场方向垂直,且线圈上、下边始终与磁场边界平行,不计空气阻力,则线圈下落过程中的v-t图象可能正确的是( )| A. |  | B. | 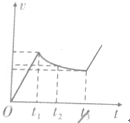 | C. | 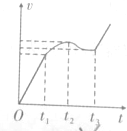 | D. | 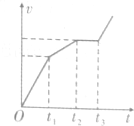 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
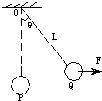 一质量为m的小球,用长为l的轻绳悬挂在O点,小球在水平拉力F作用下,从平衡位置P点缓慢地移到Q点,如图所示,则力F所做的功为( )
一质量为m的小球,用长为l的轻绳悬挂在O点,小球在水平拉力F作用下,从平衡位置P点缓慢地移到Q点,如图所示,则力F所做的功为( )| A. | mglcosθ | B. | mgl(1-cosθ) | C. | Flcosθ | D. | Flθ |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
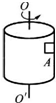 如图所示,半径为r的圆筒绕竖直中心轴OO′转动,小物块A靠在圆筒的内壁上,它与圆筒的静摩擦因数为μ,现要使A不下落,则圆筒转动的转速至少应为$\frac{{\sqrt{ug}}}{{\sqrt{4r{π^2}}}}$.
如图所示,半径为r的圆筒绕竖直中心轴OO′转动,小物块A靠在圆筒的内壁上,它与圆筒的静摩擦因数为μ,现要使A不下落,则圆筒转动的转速至少应为$\frac{{\sqrt{ug}}}{{\sqrt{4r{π^2}}}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com