
北京朝阳区初三年级综合练习(一)
数学试卷
2007.5
第I卷(共32分)
一、选择题(共8个小题,每小题4分,共32分)
1、9的平方根是
A. 3 B.
-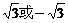
2、下列各式计算正确的是
A. 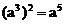 B.
B.

C. 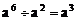 D.
D.

3、中国年水资源总量约为27500亿立方米,居世界第六位,人均占有水量仅为2400立方米左右,只相当于世界人均的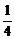 ,居世界第110位,中国已被联合国列为13个贫水国之一。将数据27500亿用科学记数法表示正确的是
,居世界第110位,中国已被联合国列为13个贫水国之一。将数据27500亿用科学记数法表示正确的是
A. 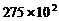 亿 B.
亿 B.
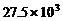 亿
亿
C. 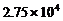 亿 D.
亿 D.
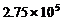 亿
亿
4、函数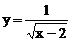 中,自变量x的取值范围是
中,自变量x的取值范围是
A.  B.
B.
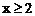 C.
C.
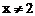 D.
D.

5、如图,AB为⊙O直径,点C、D在⊙O上,如果∠ABC=70°,那么∠D的度数为

A. 20° B. 30° C. 35° D. 70°
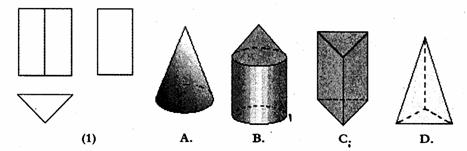
6、一个几何体的三视图如图(1)所示,那么这个几何体是
7、在Rt△ABC中,∠C=90°,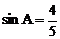 ,则
,则 的值为
的值为
A. 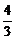 B.
B.
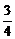 C.
C.
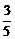 D.
D.

8、如图,下列结论中错误的是
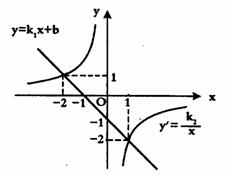
A. 方程组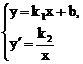 的解为
的解为
B. 当 时,有
时,有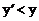
C. 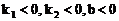
D. 直线 与两坐标轴围成的三角形的面积是
与两坐标轴围成的三角形的面积是
第II卷(共88分)
二、填空题(共4个小题,每小题4分,共16分)
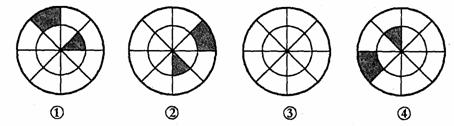
9、分析图①、②、④中阴影部分的分布规律,按此规律在图③中画出其中的阴影部分。
10、已知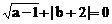 ,那么
,那么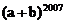 的值为
。
的值为
。
11、已知关于x的方程 有两个不相等的实数根,则m的取值范围是
。
有两个不相等的实数根,则m的取值范围是
。
12、 的圆心在x轴上,两圆交于A、B两点,若A点的坐标为(-3,1),则B点的坐标为
。
的圆心在x轴上,两圆交于A、B两点,若A点的坐标为(-3,1),则B点的坐标为
。
三、解答题(13题~22题每小题5分,23题7分,24题7分,25题8分,共72分)
13、(本小题满分5分)
计算: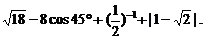
解:
14、(本小题满分5分)
因式分解:
解:
15、(本小题满分5分)
解方程: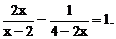
解:
16、(本小题满分5分)
如图,AC是菱形ABCD的对角线,请你在下列条件:①分别作∠BAC、∠DAC的平分线AE、AF交BC于点E,交DC于点F;②分别作AE⊥BC于点E,AF⊥DC于点F。从中任选一个作为条件,证明BE=DF。
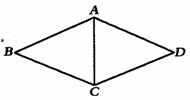
已知:如图,AC是菱形ABCD的对角线, (填写选择条件的序号)。
求证: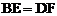 。
。
证明:
17、(本小题满分5分)
如图,要在一个三角形ABC的花坛中种满花草,工作人员沿与AB平行的方向画一条直线,将原花坛分割出一片三角形的地块,测出△CDE的面积为 ,CE长为4m,BE长为6m,请你根据测得的数据,计算出整个花坛△ABC的面积。
,CE长为4m,BE长为6m,请你根据测得的数据,计算出整个花坛△ABC的面积。
解:

18、(本小题满分5分)
为了了解学校运动队的训练情况,该校对运动队中的甲、乙两名运动员的训练进行了跟踪记录。下图是他们在同一训练项目中连续十次的测试成绩:

(1)请根据图中提供的信息填写下表:
平均数
众数
甲
乙
(2)请从平均数、众数两个角度对这两名运动员的训练成绩进行比较;
(3)请依据折线图分析哪位运动员的训练效果更好?
答:(2)
(3)
19、(本小题满分5分)
已知:如图,等边△ABC的边长为2,E为BC边的中点,分别以顶点B、C为圆心,BE、CE长为半径画弧交AB、AC于点D、F。求图中阴影部分的面积。
解:

20、(本小题满分5分)
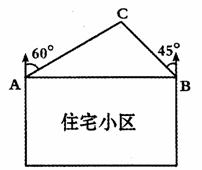
某住宅小区如图所示,小区东西两端的楼A、B之间的距离为2km,某开发商准备在位于A楼的北偏东60°方向,且在B楼的北偏西45°方向上的C处盖一个商业大厦,如果施工期间,产生的噪音会影响到方圆0.8km处,请你通过计算说明住宅小区是否会有住户受到噪音的影响。
(参考数据: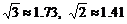 )
)
解:
21、(本小题满分5分)
袋子中装有标号分别为1号、2号、3号、4号的四个小球(它们除标号不同外,其余均相同),如果每次从袋中只摸出一个球,放回后再摸第二次,用列表或画树形图的方法求两次摸出的球恰好是2号球和3号球的概率。
解:
22、(本小题满分5分)
北京申奥成功,促进了一批产业的迅速发展。某通讯公司开发了一种新型通讯产品投放市场,根据计划,第一年投入资金600万元,第二年比第一年减少 ,第三年比第二年减少
,第三年比第二年减少 。该产品第一年收入资金约为400万元,公司计划三年内不仅要将投入的总资金全部收回,还要盈利
。该产品第一年收入资金约为400万元,公司计划三年内不仅要将投入的总资金全部收回,还要盈利 ,要实现这一目标,该产品收入的年平均增长率约是多少?
,要实现这一目标,该产品收入的年平均增长率约是多少?
(结果精确到0.1,参考数据: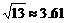 )
)
解:
23、(本小题满分7分)
已知:如图,点O是四边形BCED外接圆的圆心,点O在BC上,点A在CB的延长线上,且∠ADB=∠DEB,EF⊥BC于点F,交⊙O于点M, 。
。
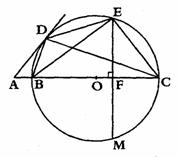
(1)求证:AD是⊙O的切线;
(2)若 上有一动点P,且
上有一动点P,且 ,求⊙O直径的长;
,求⊙O直径的长;
(3)在(2)的条件下,如果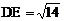 ,求
,求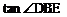 的值。
的值。
24、(本小题满分7分)
已知:如图①,△ABC是等边三角形,四边形BDEF是菱形,其中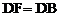 ,连接AF、CD。
,连接AF、CD。

(1)观察图形①,猜想AF与CD之间有怎样的数量关系?直接写出结论,不必证明;
(2)将菱形BDEF绕点B按顺时针方向旋转,使菱形BDEF的一边落在等边△ABC内部,在图②中画出一个变换后的图形,并对照已知图形标记字母,请问:(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)在上述旋转过程中,AF与CD所夹锐角的度数是否发生变化?若不变,请你求出它的度数,并说明理由;若改变,请说明它的度数是如何变化的。
25、(本小题满分8分)
已知抛物线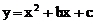 经过坐标原点,且在x轴的正半轴上截得的线段长为4,对称轴为直线
经过坐标原点,且在x轴的正半轴上截得的线段长为4,对称轴为直线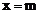 直线绕点A(m,0)旋转,交抛物线于点B(x,y),交y轴负半轴于点C,过点C且平行于x轴的直线与直线
直线绕点A(m,0)旋转,交抛物线于点B(x,y),交y轴负半轴于点C,过点C且平行于x轴的直线与直线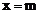 交于点D,设△AOB的面积为
交于点D,设△AOB的面积为 ,△ABD的面积为
,△ABD的面积为 。
。
(1)求这条抛物线的顶点坐标;
(2)判断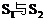 的大小关系,并证明你的结论。
的大小关系,并证明你的结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com