
2007-2008学年度滕州市第一学期期中考试
九年级数学试题
一、选择题:每小题3分,共45分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列说法正确的是
A.等腰三角形一定是锐角三角形
B.等腰三角形的腰长总大于底边长
C.等腰三角形底角的外角一定是钝角
D.顶角相等的两个等腰三角形是全等三角形
2.下列说法错误的是
A.任何命题都有逆命题 B.定理都有逆定理
C.命题的逆命题不一定是正确的 D.定理的逆定理一定是正确的
3.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,DE是斜边AB的垂直平分线,且DE=
A.

4.到△ABC的三个顶点距离相等的点是△ABC的
A.三条中线的交点 B.三条角平分线的交点
C.三条高线的交点 D.三条边的垂直平分线的交点
5.如图,△ABC为等边三角形,过点B做BD⊥BC,过点A做AD⊥BD,垂足分别为B、D,已知等边三角形的周长为m,则AD长为
A.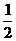 m B.
m B. m
C.
m
C. m D.
m D. m
m

6.下列方程:①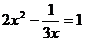 ;②
;② ;③
;③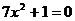 ;④
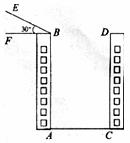
;④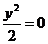 中,是一元二次方程有
中,是一元二次方程有
A.①和② B.②和③ C.③和④ D.①和③
7.把方程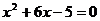 左边配成完全平方后,所得方程为
左边配成完全平方后,所得方程为
A.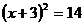 B.
B.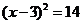 C.
C.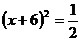 D.以上答案都不对
D.以上答案都不对
8.三角形两边的长分别是8和6,第三边的长是一元二次方程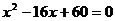 一个实数根,则该三角形的周长是
一个实数根,则该三角形的周长是
A.24 B.24或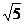 C.24或20
D.8
C.24或20
D.8
9.以正方形ABCD的一组邻边AD、CD向形外作等边三角形ADE、CDF,则下列结论中错误的是
A.BD平分∠EBF B.∠DEF=30° C.BD⊥EF D.∠BFD=45°
10.正方形具有而菱形不具有的性质是
A.四个角都是直角 B.两组对边分别相等
C.内角和为360° D.对角线平分对角
11.下面四幅图是两个物体不同时刻在太阳光下的影子,按照时间先后顺序正确的是

A.a→b→c→d B.d→b→c→a
C.c→d→a→b D.a→c→b→d
12.如图所示的几何体的俯视图是
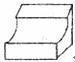

13.如图,在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F的度数为
A.110° B.70° C.50° D.30°
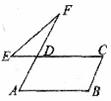
14.若点M,N,P,Q分别是四边形ABCD四边的中点,下列4个命题中,正确的个数有
①四边形MNPQ是梯形;
②当四边形ABCD的对角线相等时,四边形MNPQ是菱形;
③当四边形ABCD的对角线垂直时,四边形MNPQ是矩形;
④当四边形ABCD的对角线相等且垂直时,四边形MNPQ是正方形
A.1个 B.2个 C.3个 D.4个
15.已知△ABC的周长为l,连接△ABC三边的中点,构成第二个三角形,再连接第二个三角形三边的中点,构成第三个三角形,……,依次类推,第2007个三角形的周长为
A.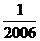 B.
B.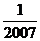 C.
C.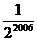 D.
D.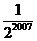
二、填空题:每小题3分,共24分。把答案填在题中横线上。
16.当k _____________时,方程 是关于
是关于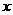 的一元二次方程。
的一元二次方程。
17.方程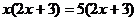 的根是_____________。
的根是_____________。
18.在△ABC中,AB=3,AC=4,BC=5,则△ABC的面积是_____。
19.菱形的两条对角线的长分别是6 cm和8 cm,则这个菱形的周长为_____。
20.用反证法证明“三角形中必有一个内角不小于60°”,应当先假设这个三角形中
______________。
21.如图,延长正方形ABCD的边AB到E,使BE=AC,则∠E=____。

22.某药品原价每盒25元,为了响应国家解决老百姓看病难的号召,经过连续两次降价,现在每盒售价l6元,则该药品平均每次降价的百分率是__________________ 。
23.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够,一位同学帮他想了一个主意,先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为15米,则AB两点问的距离__________。

三、解答题:本大题共5小题,满分51分,解答应写出文字说明、说理过程或演算步骤。
24.(每小题5分,计l0分)解方程:
(1) :
:
(2)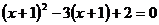
25.(6分)如图,在△ABC中,AB=AC,D为底边BC的中点,DE⊥AB于点E,DF⊥AC于点F。
求证:DE=DF
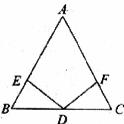
26.(6分)如图,在Rt△ABC中,∠ACB=90°,∠CAB=30°用圆规和直尺作图,用两种方法把它分成两个三角形,且要求其中一个三角形是等腰三角形.(保留作图痕迹,不要求写作法和证明)
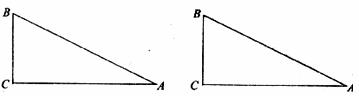
27.(7分)如图,AB、CD为住宅区的两幢楼,它们的高均为36米,两楼间的距AC为21米.现需要了解甲楼对乙楼的采光的影响情况,当太阳光与水平线的夹角为30°时,求甲楼的影子落在乙楼上有多高?(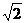 =1.41,
=1.41,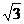 =1.73,精确到0.1米)
=1.73,精确到0.1米)
28.(10分)如图所示,甲、乙两人分别从正方形广场ABCD的顶点B、C两点同时出发,甲由C向D运动,乙由B向C运动,甲的速度为l千米/分,乙的速度为2千米/分,若正方形广场的周长为40千米,问几分钟后,两人相距2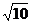 千米?
千米?
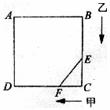
29.(12分)在△ABC中,点O是AC上的一个动点,过点O作MN//BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F。
(1)请猜测OE与OF的大小关系,并说明你的理由;
(2)点O运动到何处时,四边形AECF是矩形?写出推理过程;
(3)在什么条件下,四边形AECF是正方形?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com