
2008年南京市初中毕业生学业考试
数学试卷
一、选择题(本大题共10小题,每小题2分,共计20分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的序号填涂在答题卡上)
1. 的绝对值是( )
的绝对值是( )
A. B.
B. C.
C.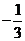 D.
D.
2.
A. B.
B. C.
C. D.
D.
3.计算 的结果是( )
的结果是( )
A. B.
B. C.
C. D.
D.
4.2的平方根是( )
A.4 B.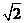 C.
C. D.
D.
5.已知反比例函数的图象经过点 ,则这个函数的图象位于( )
,则这个函数的图象位于( )
A.第一、三象限 B.第二、三象限
C.第二、四象限 D.第三、四象限
6.如图,将一张等腰梯形纸片沿中位线剪开,拼成一个新的图形,这个新的图形可以是下列图形中的( )

A.三角形 B.平行四边形 C.矩形 D.正方形
7.小刚身高
A.
8.如图,⊙ 是等边三角形
是等边三角形 的外接圆,⊙
的外接圆,⊙ 的半径为2,则等边三角形
的半径为2,则等边三角形 的边长为( )
的边长为( )

A. B.
B. C.
C. D.
D.
9.超市为了制定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间6分钟到7分钟表示大于或等于6分钟而小于7分钟,其它类同).这个时间段内顾客等待时间不少于6分钟的人数为( )
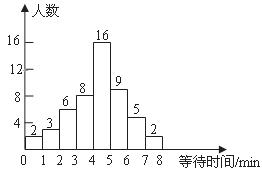
A.5 B.
10.如图,已知⊙ 的半径为1,
的半径为1, 与⊙
与⊙ 相切于点
相切于点 ,
, 与⊙
与⊙ 交于点
交于点 ,
,  ,
,
垂足为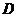 ,则
,则 的值等于( )
的值等于( )

A. B.
B. C.
C. D.
D.
二、填空题(本大题共6小题,每小题3分,共计18分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
11.计算 的结果是
.
的结果是
.
12.函数 中,自变量
中,自变量 的取值范围是
.
的取值范围是
.
13.已知⊙ 和⊙
和⊙ 的半径分别为3cm和5cm,且它们内切,则圆心距
的半径分别为3cm和5cm,且它们内切,则圆心距 等于 cm.
等于 cm.
14.若等腰三角形的一个外角为 ,则它的底角为 度.
,则它的底角为 度.
15.口袋内装有一些除颜色外完全相同的红球、白球和黑球,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么摸出黑球的概率是 .
16.如图,有一圆形展厅,在其圆形边缘上的点 处安装了一台监视器,它的监控角度是
处安装了一台监视器,它的监控角度是 .为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器 台.
.为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器 台.

三、解答题(本大题共12小题,共计82分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
17.(6分)先化简,再求值: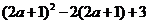 ,其中
,其中 .
.
18.(6分)解方程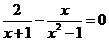 .
.
19.(6分)解不等式组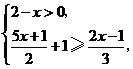 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.

20.(6分)我国从2008年6月1日起执行“限塑令”.“限塑令”执行前,某校为了了解本校学生所在家庭使用塑料袋的数量情况,随机调查了10名学生所在家庭月使用塑料袋的数量,结果如下(单位:只)
65,70,85,75,85,79,74,91,81,95.
(1)计算这10名学生所在家庭平均月使用塑料袋多少只?
(2)“限塑令”执行后,家庭月使用塑料袋数量预计将减少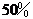 .根据上面的计算结果,估计该校1 000名学生所在家庭月使用塑料袋可减少多少只?
.根据上面的计算结果,估计该校1 000名学生所在家庭月使用塑料袋可减少多少只?
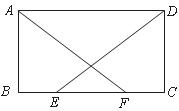
21.(6分)如图,在四边形ABCD中,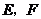 为
为 上两点,且
上两点,且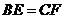 ,
,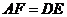 .
.
求证:(1)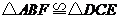 ;
;
(2)四边形 是矩形.
是矩形.
22.(6分)如图,菱形 (图1)与菱形
(图1)与菱形 (图2)的形状、大小完全相同.
(图2)的形状、大小完全相同.
(1)请从下列序号中选择正确选项的序号填写;
①点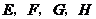 ;②点
;②点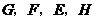 ;③点
;③点 ;④点
;④点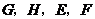 .
.
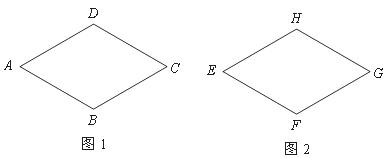
如果图1经过一次平移后得到图2,那么点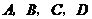 对应点分别是
;
对应点分别是
;
如果图1经过一次轴对称后得到图2,那么点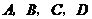 对应点分别是
;
对应点分别是
;
如果图1经过一次旋转后得到图2,那么点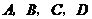 对应点分别是
;
对应点分别是
;
(2)①图1,图2关于点 成中心对称,请画出对称中心(保留画图痕迹,不写画法);
成中心对称,请画出对称中心(保留画图痕迹,不写画法);
②写出两个图形成中心对称的一条性质: .(可以结合所画图形叙述)
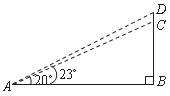
23.(6分)如图,山顶建有一座铁塔,塔高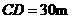 ,某人在点
,某人在点 处测得塔底
处测得塔底 的仰角为
的仰角为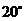 ,塔顶
,塔顶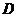 的仰角为
的仰角为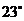 ,求此人距
,求此人距 的水平距离
的水平距离 .
.
(参考数据: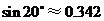 ,
,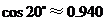 ,
,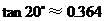 ,
,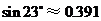 ,
,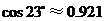 ,
,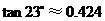 )
)
24.(7分)小明和小颖做掷骰子的游戏,规则如下:
①游戏前,每人选一个数字;
②每次同时掷两枚均匀骰子;
③如果同时掷得的两枚骰子点数之和,与谁所选数字相同,那么谁就获胜.
(1)在下表中列出同时掷两枚均匀骰子所有可能出现的结果:

(2)小明选的数字是5,小颖选的数字是6.如果你也加入游戏,你会选什么数字,使自己获胜的概率比他们大?请说明理由.
25.(7分)某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为 .在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是
.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是 ?
?

26.(8分)已知二次函数 中,函数
中,函数 与自变量
与自变量 的部分对应值如下表:
的部分对应值如下表:

…



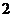

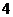
…

…
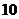
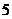
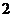

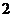
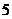
…
(1)求该二次函数的关系式;
(2)当 为何值时,
为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
(3)若 ,
, 两点都在该函数的图象上,试比较
两点都在该函数的图象上,试比较 与
与 的大小.
的大小.
27.(8分)如图,已知⊙ 的半径为6cm,射线
的半径为6cm,射线 经过点
经过点 ,
, ,射线
,射线 与⊙
与⊙ 相切于点
相切于点 .
. 两点同时从点
两点同时从点 出发,点
出发,点 以5cm/s的速度沿射线
以5cm/s的速度沿射线 方向运动,点
方向运动,点 以4cm/s的速度沿射线
以4cm/s的速度沿射线 方向运动.设运动时间为
方向运动.设运动时间为 s.
s.
(1)求 的长;
的长;
(2)当 为何值时,直线
为何值时,直线 与⊙
与⊙ 相切?
相切?

28.(10分)一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为 ,两车之间的距离为
,两车之间的距离为 ,图中的折线表示
,图中的折线表示 与
与 之间的函数关系.
之间的函数关系.
根据图象进行以下探究:
信息读取
(1)甲、乙两地之间的距离为 km;
(2)请解释图中点 的实际意义;
的实际意义;

图象理解
(3)求慢车和快车的速度;
(4)求线段 所表示的
所表示的 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
问题解决:
(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com