
2008年仙桃四市初中毕业生学业考试
数学试卷
一、选择题(本大题共有8个小题,每小题3分,满分24分.)
1. 的倒数是( )
的倒数是( )
A.2
B. C.
C. D.
D.
2.
A.  B.
B.  C.
C.  D.
D. 
3.在下面的四个几何体中,它们各自的左视图与主视图不相同的是 ( )

4.对于反比例函数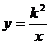 (
( ),下列说法不正确的是(
)
),下列说法不正确的是(
)
A.它的图象分布在第一、三象限 B.点(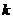 ,
,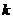 )在它的图象上
)在它的图象上
C.它的图象是中心对称图形 D. 随
随 的增大而增大
的增大而增大
5.如图,四边形 是菱形,过点
是菱形,过点 作
作 的平行线交
的平行线交 的延长线于点
的延长线于点 ,则下列式子不成立的是( )
,则下列式子不成立的是( )

A.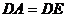 B.
B.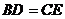 C.
C.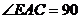 ° D.
° D.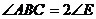
6.如图,抛物线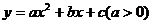 的对称轴是直线
的对称轴是直线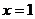 ,且经过点
,且经过点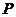 (3,0),则
(3,0),则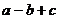 的值为 ( )
的值为 ( )
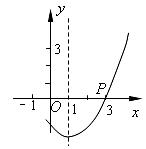
A.0 B.-
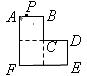
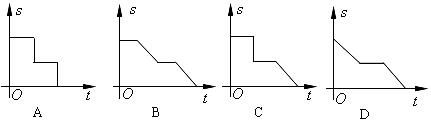
7.如图,三个大小相同的正方形拼成六边形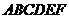 ,一动点
,一动点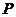 从点
从点 出发沿着
出发沿着 →
→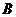 →
→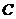 →
→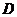 →
→ 方向匀速运动,最后到达点
方向匀速运动,最后到达点 .运动过程中
.运动过程中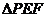 的面积(
的面积(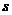 )随时间(t)变化的图象大致是( )
)随时间(t)变化的图象大致是( )
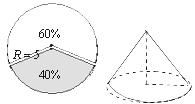
8.如图,小明从半径为5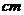 的圆形纸片中剪下40%圆周的一个扇形,然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为(
)
的圆形纸片中剪下40%圆周的一个扇形,然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为(
)
A.3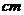 B.
B.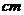

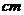 D.
D.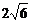
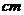
二、填空题(本大题共8个小题,每小题3分,满分24分)将结果直接填写在每题的横线上.
9.分解因式: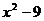 = .
= .
10.化简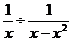 的结果是
.
的结果是
.
11. “五一”期间,某服装商店举行促销活动,全部商品八折销售.小华购买一件标价为180
元的运动服,打折后他比按标价购买节省了 元.
12. 关于 的一元二次方程
的一元二次方程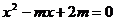 的一个根为1,则方程的另一根为 .
的一个根为1,则方程的另一根为 .
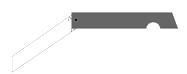
13.如图是我们生活中经常接触的小刀,刀柄外形是一个直角梯形(下底挖去一小半圆),刀片上、下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2= 度.
14.
15.如图,矩形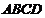 的面积为5,它的两条对角线交于点
的面积为5,它的两条对角线交于点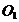 ,以
,以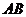 、
、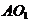 为两邻边作
为两邻边作
平行四边形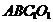 ,平行四边形
,平行四边形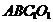 的对角线交于点
的对角线交于点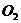 ,同样以
,同样以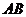 、
、
为两邻边作平行四边形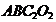 ,……,依次类推,则平行四边形
,……,依次类推,则平行四边形 的面积
的面积
为 .
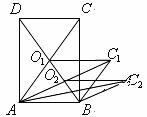
16.如图, 中,点
中,点 的坐标为(0,1),点
的坐标为(0,1),点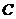 的坐标为(4,3),如果要使
的坐标为(4,3),如果要使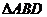 与
与 全等,那么点
全等,那么点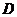 的坐标是 .
的坐标是 .
三、解答题(本大题共9个小题,满分72分.)
17.(本题满分5分)
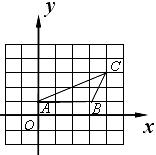
计算:
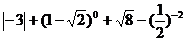
18.(本题满分5分)
解不等式组 并把解集表示在下面的数轴上.
并把解集表示在下面的数轴上.
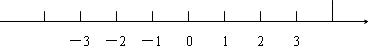
19. (本题满分7分)
为了降低能源消耗,减少环境污染,国务院办公厅下发了“关于限制生产销售使用塑料购物袋的通知”(简称“限塑令”),并从
(1)这次调查的购物者总人数是 ;
(2)请补全条形统计图,并说明扇形统计图中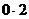 元部分所对应的圆心角是
度0.3元部分所对应的圆心角是
度;
元部分所对应的圆心角是
度0.3元部分所对应的圆心角是
度;
(3)若
并根据调查情况,谈谈你的看法.

20.(本题满分7分)
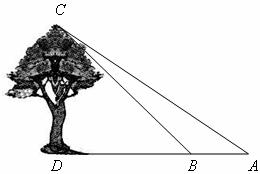
在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:
(1)在大树前的平地上选择一点 ,测得由点A看大树顶端
,测得由点A看大树顶端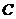 的仰角为35°;
的仰角为35°;
(2)在点 和大树之间选择一点
和大树之间选择一点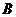 (
( 、
、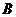 、
、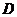 在同一直线上),测得由点
在同一直线上),测得由点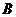 看大树顶端
看大树顶端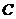 的仰角恰好为45°;
的仰角恰好为45°;
(3)量出 、
、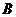 两点间的距离为
两点间的距离为 的高度.
的高度.
(可能用到的参考数据:sin35°≈0.57 cos35°≈0.82 tan35°≈0.70)
21. (本题满分8分)
 箱中装有3张相同的卡片,它们分别写有数字1,2,4;
箱中装有3张相同的卡片,它们分别写有数字1,2,4;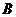 箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从
箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从 箱、
箱、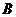 箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
(1)两张卡片上的数字恰好相同的概率.
(2)如果取出 箱中卡片上的数字作为十位上的数字,取出
箱中卡片上的数字作为十位上的数字,取出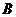 箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
22. (本题满分8分)
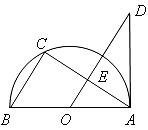
如图,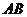 为半圆
为半圆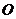 的直径,点C在半圆
的直径,点C在半圆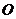 上,过点
上,过点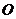 作
作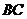 的平行线交
的平行线交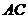 于点
于点 ,交过点
,交过点 的直线于点
的直线于点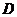 ,且
,且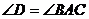 .
.
(1)求证: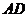 是半圆O的切线;
是半圆O的切线;
(2)若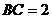 ,
,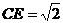 ,求
,求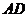 的长.
的长.
23. (本题满分10分)
小华将一张矩形纸片(如图1)沿对角线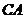 剪开,得到两张三角形纸片(如图2),其中
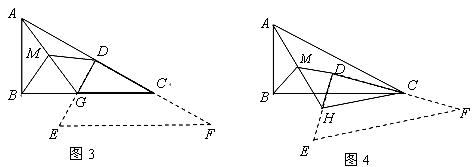
剪开,得到两张三角形纸片(如图2),其中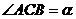 ,然后将这两张三角形纸片按如图3所示的位置摆放,
,然后将这两张三角形纸片按如图3所示的位置摆放,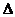
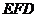 纸片的直角顶点
纸片的直角顶点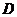 落在
落在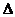
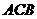 纸片的斜边
纸片的斜边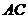 上,直角边
上,直角边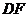 落在
落在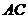 所在的直线上.
所在的直线上.
(1)
若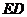 与
与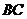 相交于点
相交于点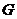 ,取
,取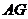 的中点
的中点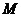 ,连接
,连接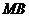 、
、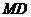 ,当
,当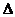
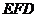 纸片沿
纸片沿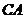 方向平移时(如图3),请你观察、测量
方向平移时(如图3),请你观察、测量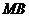 、
、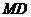 的长度,猜想并写出
的长度,猜想并写出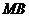 与
与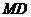 的数量关系,然后证明你的猜想;
的数量关系,然后证明你的猜想;
(2)
在(1)的条件下,求出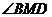 的大小(用含
的大小(用含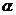 的式子表示),并说明当
的式子表示),并说明当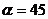 °时,
°时, 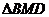 是什么三角形?
是什么三角形?
(3)
在图3的基础上,将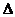
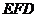 纸片绕点
纸片绕点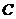 逆时针旋转一定的角度(旋转角度小于90°),此时
逆时针旋转一定的角度(旋转角度小于90°),此时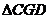 变成
变成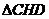 ,同样取
,同样取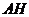 的中点
的中点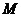 ,连接
,连接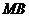 、
、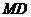 (如图4),请继续探究
(如图4),请继续探究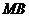 与
与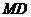 的数量关系和
的数量关系和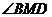 的大小,直接写出你的猜想,不需要证明,并说明
的大小,直接写出你的猜想,不需要证明,并说明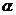 为何值时,
为何值时,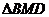 为等边三角形.
为等边三角形.

24.(本题满分10分)
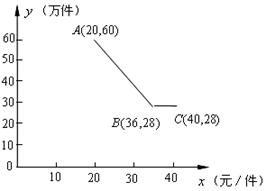
华宇公司获得授权生产某种奥运纪念品,经市场调查分析,该纪念品的销售量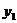 (万件)与纪念品的价格
(万件)与纪念品的价格 (元/件)之间的函数图象如图所示,该公司纪念品的生产数量
(元/件)之间的函数图象如图所示,该公司纪念品的生产数量 (万件)与纪念品的价格
(万件)与纪念品的价格 (元/件)近似满足函数关系式
(元/件)近似满足函数关系式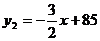 .,若每件纪念品的价格不小于20元,且不大于40元.请解答下列问题:
.,若每件纪念品的价格不小于20元,且不大于40元.请解答下列问题:
(1)
求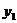 与
与 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(2)
当价格 为何值时,使得纪念品产销平衡(生产量与销售量相等);
为何值时,使得纪念品产销平衡(生产量与销售量相等);
(3) 当生产量低于销售量时,政府常通过向公司补贴纪念品的价格差来提高生产,促成新的产销平衡.若要使新的产销平衡时销售量达到46万件,政府应对该纪念品每件补贴多少元?
25.(本题满分12分)
如图,直角梯形 中,
中,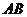 ∥
∥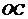 ,
,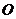 为坐标原点,点
为坐标原点,点 在
在 轴正半轴上,点
轴正半轴上,点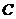 在
在 轴正半轴上,点
轴正半轴上,点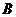 坐标为(2,2
坐标为(2,2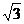 ),∠
),∠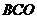 = 60°,
= 60°,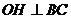 于点
于点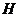 .动点
.动点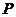 从点
从点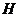 出发,沿线段
出发,沿线段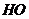 向点
向点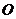 运动,动点
运动,动点 从点
从点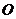 出发,沿线段
出发,沿线段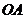 向点
向点 运动,两点同时出发,速度都为每秒1个单位长度.设点
运动,两点同时出发,速度都为每秒1个单位长度.设点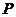 运动的时间为
运动的时间为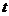 秒.
秒.
(1)
求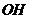 的长;
的长;
(2)
若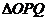 的面积为
的面积为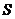 (平方单位).
求
(平方单位).
求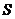 与
与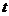 之间的函数关系式.并求
之间的函数关系式.并求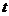 为何值时,
为何值时,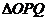 的面积最大,最大值是多少?
的面积最大,最大值是多少?
(3)
设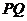 与
与 交于点
交于点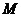 .①当△
.①当△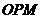 为等腰三角形时,求(2)中
为等腰三角形时,求(2)中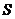 的值.
的值.
②探究线段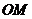 长度的最大值是多少,直接写出结论.
长度的最大值是多少,直接写出结论.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com