
2008年北京市中考试卷分析(数学)
一、选择题(共8道小题,每小题4分,共32分)
1.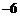 的绝对值等于( )
的绝对值等于( )
A.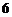 B.
B.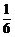 C.
C.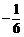 D.
D.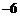
2.截止到
A.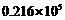 B.
B.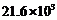 C.
C.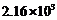 D.
D.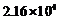
3.若两圆的半径分别是
A.内切 B.相交 C.外切 D.外离
4.众志成城,抗震救灾.某小组7名同学积极捐出自己的零花钱支援灾区,他们捐款的数额分别是(单位:元):50,20,50,30,50,25,135.这组数据的众数和中位数分别是( )
A.50,20 B.50,
5.若一个多边形的内角和等于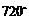 ,则这个多边形的边数是( )
,则这个多边形的边数是( )
A.5 B.6 C.7 D.8
6.如图,有5张形状、大小、质地均相同的卡片,正面分别印有北京奥运会的会徽、吉祥物(福娃)、火炬和奖牌等四种不同的图案,背面完全相同.现将这5张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面图案恰好是吉祥物(福娃)的概率是( )

A.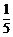 B.
B.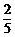 C.
C.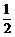 D.
D.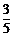
7.若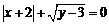 ,则
,则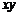 的值为( )
的值为( )
A.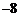 B.
B.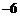 C.
C. D.
D.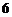
8.已知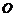 为圆锥的顶点,
为圆锥的顶点,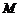 为圆锥底面上一点,点
为圆锥底面上一点,点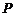 在
在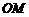 上.一只蜗牛从
上.一只蜗牛从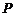 点出发,绕圆锥侧面爬行,回到
点出发,绕圆锥侧面爬行,回到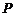 点时所爬过的最短路线的痕迹如右图所示.若沿
点时所爬过的最短路线的痕迹如右图所示.若沿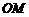 将圆锥侧面剪开并展开,所得侧面展开图是( )
将圆锥侧面剪开并展开,所得侧面展开图是( )
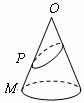
二、填空题(共4道小题,每小题4分,共16分)
9.在函数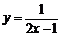 中,自变量
中,自变量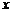 的取值范围是
.
的取值范围是
.
10.分解因式: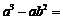 .
.
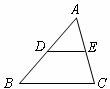
11.如图,在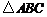 中,
中,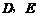 分别是
分别是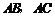 的中点,若
的中点,若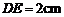 ,则
,则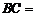 cm.
cm.
12.一组按规律排列的式子: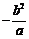 ,
,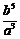 ,
,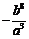 ,
,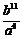 ,…(
,…(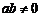 ),其中第7个式子是 ,第
),其中第7个式子是 ,第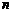 个式子是 (
个式子是 (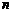 为正整数).
为正整数).
三、解答题(共5道小题,共25分)
13.(本小题满分5分)
计算: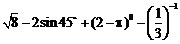 .
.
14.(本小题满分5分)
解不等式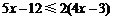 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
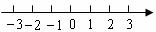
15.(本小题满分5分)
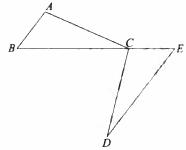
已知:如图,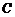 为
为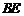 上一点,点
上一点,点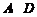 分别在
分别在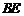 两侧.
两侧.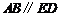 ,
,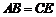 ,
,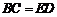 .求证:
.求证: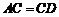 .
.
16.(本小题满分5分)
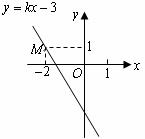
如图,已知直线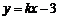 经过点
经过点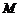 ,求此直线与
,求此直线与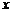 轴,
轴,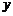 轴的交点坐标.
轴的交点坐标.
17.(本小题满分5分)
已知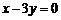 ,求
,求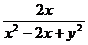 的值.
的值.
四、解答题(共2道小题,共10分)
18.(本小题满分5分)
如图,在梯形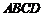 中,
中,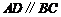 ,
,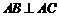 ,
,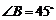 ,
,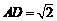 ,
,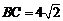 ,求
,求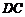 的长.
的长.
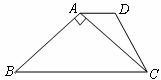
19.(本小题满分5分)
已知:如图,在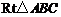 中,
中,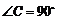 ,点
,点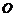 在
在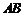 上,以
上,以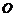 为圆心,
为圆心,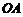 长为半径的圆与
长为半径的圆与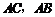 分别交于点
分别交于点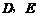 ,且
,且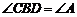 .
.
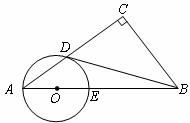
(1)判断直线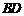 与⊙O的位置关系,并证明你的结论;
与⊙O的位置关系,并证明你的结论;
(2)若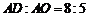 ,
,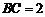 ,求
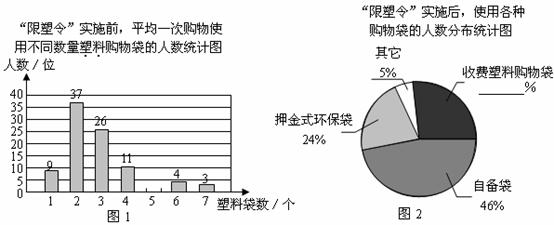
,求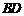 的长.
的长.
五、解答题(本题满分6分)
20.为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分:
“限塑令”实施后,塑料购物袋使用后的处理方式统计表
处理方式
直接丢弃
直接做垃圾袋
再次购物使用
其它
选该项的人数占
总人数的百分比
5%
35%
49%
11%
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,如果每天约有2000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.
六、解答题(共2道小题,共9分)
21.(本小题满分5分)列方程或方程组解应用题:
京津城际铁路将于2008年8月1日开通运营,预计高速列车在北京、天津间单程直达运行时间为半小时.某次试车时,试验列车由北京到天津的行驶时间比预计时间多用了6分钟,由天津返回北京的行驶时间与预计时间相同.如果这次试车时,由天津返回北京比去天津时平均每小时多行驶40千米,那么这次试车时由北京到天津的平均速度是每小时多少千米?
22.(本小题满分4分)
已知等边三角形纸片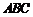 的边长为
的边长为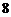 ,
, 为
为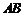 边上的点,过点
边上的点,过点 作
作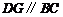 交
交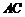 于点
于点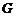 .
.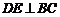 于点
于点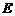 ,过点
,过点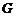 作
作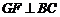 于点
于点 ,把三角形纸片
,把三角形纸片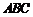 分别沿
分别沿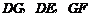 按图1所示方式折叠,点
按图1所示方式折叠,点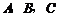 分别落在点
分别落在点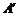 ,
,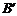 ,
,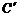 处.若点
处.若点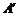 ,
,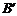 ,
,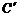 在矩形
在矩形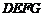 内或其边上,且互不重合,此时我们称
内或其边上,且互不重合,此时我们称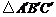 (即图中阴影部分)为“重叠三角形”.
(即图中阴影部分)为“重叠三角形”.
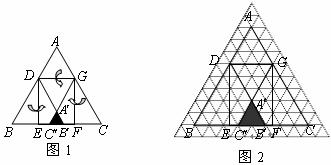
(1)若把三角形纸片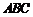 放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点
放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点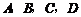 恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形
恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形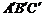 的面积;
的面积;
(2)实验探究:设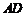 的长为
的长为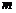 ,若重叠三角形
,若重叠三角形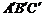 存在.试用含
存在.试用含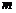 的代数式表示重叠三角形
的代数式表示重叠三角形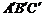 的面积,并写出
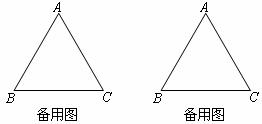
的面积,并写出 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).
七、解答题(本题满分7分)
23.已知:关于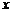 的一元二次方程
的一元二次方程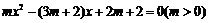 .
.
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为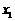 ,
,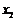 (其中
(其中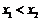 ).若
).若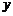 是关于
是关于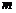 的函数,且
的函数,且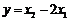 ,求这个函数的解析式;
,求这个函数的解析式;
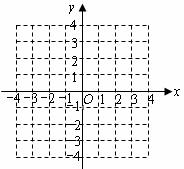
(3)在(2)的条件下,结合函数的图象回答:当自变量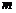 的取值范围满足什么条件时,
的取值范围满足什么条件时,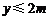 .
.
八、解答题(本题满分7分)
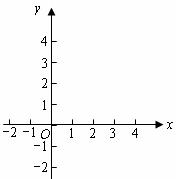
24.在平面直角坐标系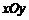 中,抛物线
中,抛物线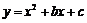 与
与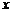 轴交于
轴交于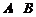 两点(点
两点(点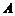 在点
在点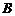 的左侧),与
的左侧),与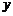 轴交于点
轴交于点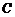 ,点
,点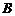 的坐标为
的坐标为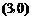 ,将直线
,将直线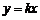 沿
沿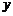 轴向上平移3个单位长度后恰好经过
轴向上平移3个单位长度后恰好经过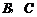 两点.
两点.
(1)求直线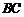 及抛物线的解析式;
及抛物线的解析式;
(2)设抛物线的顶点为 ,点
,点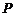 在抛物线的对称轴上,且
在抛物线的对称轴上,且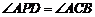 ,求点
,求点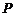 的坐标;
的坐标;
(3)连结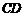 ,求
,求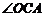 与
与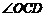 两角和的度数.
两角和的度数.
九、解答题(本题满分8分)
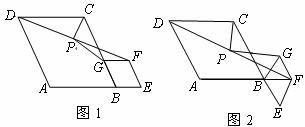
问题:如图1,在菱形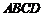 和菱形
和菱形 中,点
中,点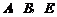 在同一条直线上,
在同一条直线上,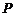 是线段
是线段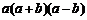 的中点,连结
的中点,连结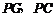 .若
.若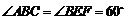 ,探究
,探究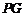 与
与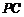 的位置关系及
的位置关系及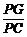 的值.
的值.
小聪同学的思路是:延长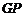 交
交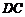 于点
于点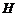 ,构造全等三角形,经过推理使问题得到解决.
,构造全等三角形,经过推理使问题得到解决.
请你参考小聪同学的思路,探究并解决下列问题:
(1)写出上面问题中线段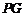 与
与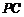 的位置关系及
的位置关系及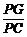 的值;
的值;
(2)将图1中的菱形 绕点
绕点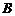 顺时针旋转,使菱形
顺时针旋转,使菱形 的对角线
的对角线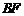 恰好与菱形
恰好与菱形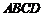 的边
的边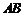 在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
(3)若图1中 ,将菱形
,将菱形 绕点
绕点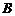 顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出
顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出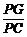 的值(用含
的值(用含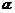 的式子表示).
的式子表示).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com