
2008年湖北省荆门市初中毕业生学业考试
数学试卷
一、选择题(本大题共10小题,每小题2分,共20分)
1.4-(-7)等于
(A) 3. (B) 11. (C) -3. (D) -11.
2.下列各式中,不成立的是
(A) 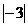 =3. (B) -
=3. (B) -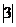 =-3. (C)
=-3. (C) 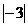 =
=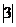 . (D) -
. (D) -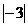 =3.
=3.
3.某住宅小区六月份中1日至6日每天用水量变化情况如折线图所示,那么这6天的平均用水量是
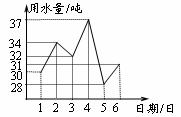
(A) 30吨. (B) 31 吨. (C) 32吨. (D) 33吨.
4.如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是
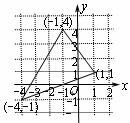
(A) (1, 7) , (-2, 2),(3, 4). (B) (1, 7) , (-2, 2),(4, 3).
(C) (1, 7) , (2, 2),(3, 4). (D) (1, 7) , (2,-2),(3, 3).
5.计算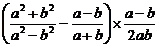 的结果是
的结果是
(A) 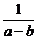 . (B)
. (B) 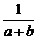 . (C) a-b. (D) a+b.
. (C) a-b. (D) a+b.
6.如图,将圆沿AB折叠后,圆弧恰好经过圆心,则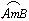 等于
等于
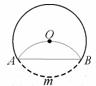
(A) 60°. (B) 90°. (C)120°. (D)150°.
7.左下图是由若干个小正方形所搭成的几何体及从上面看这个几何体所看到的图形,那么从左边看这个几何体时, 所看到的几何图形是
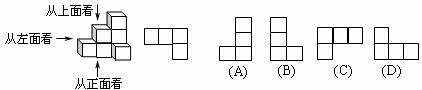
8.科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为
(A)
9.把抛物线y=x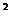 +bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y=x
+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y=x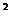 -3x+5,则
-3x+5,则
(A) b=3,c=7. (B) b=6,c=3. (C) b=-9,c=-5.(D) b=-9,c=21.
10.用四个全等的矩形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是144,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则下列关系式中不正确的是
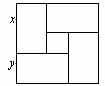
(A) x+y=12 . (B) x-y=2.
(C)
xy=35. (D) x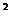 +y
+y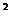 =144.
=144.
二、填空题(本大题共10小题,每小题3分,共30分)
11.  = ___________.
= ___________.
12.如图,半圆的直径AB=__________.

13.如图,l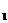 ∥l
∥l ,∠α=__________度.
,∠α=__________度.
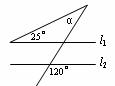
14.计算: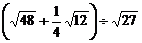 =_________.
=_________.
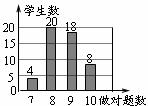
15.数学老师布置10道选择题作为课堂练习,科代表将全班同学的答题情况绘制成条形统计图,根据图中信息,全班每位同学答对题数的中位数和众数分别为______________.
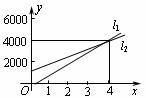
16.如图,l1反映了某公司的销售收入与销量的关系,l2 反映了该公司产品的销售成本与销量的关系,当该公司赢利(收入大于成本)时,销售量必须____________.
17.如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是_____________.

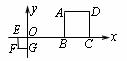
18.如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为________.

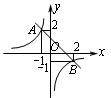
19.如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是_____________.
20.如图,正方形ABCD和正方形OEFG中, 点A和点F的坐标分别为 (3,2),(-1,-1),则两个正方形的位似中心的坐标是_________.
三、解答题(本大题共8小题,共70分)
21.(本小题满分6分)
给出三个多项式X =
22.(本小题满分6分)
今年5月12日,四川省汶川发生8.0级大地震,某中学师生自愿捐款,已知第一天捐款4800元,第二天捐款6000元,第二天捐款人数比第一天捐款人数多50人,且两天人均捐款数相等,那么两天共参加捐款的人数是多少?人均捐款多少元?
23.(本小题满分8分)
将两块全等的含30°角的三角尺如图(1)摆放在一起,它们的较短直角边长为3.
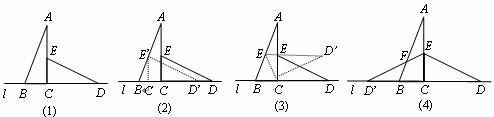
(1) 将△ECD沿直线l向左平移到图(2)的位置,使E点落在AB上,则CC′=______;
(2) 将△ECD绕点C逆时针旋转到图(3)的位置,使点E落在AB上,则△ECD绕点C旋转的度数=______;
(3) 将△ECD沿直线AC翻折到图(4)的位置,ED′与AB相交于点F,求证AF=FD′.
24.(本小题满分8分)
如图,山脚下有一棵树AB,小华从点B沿山坡向上走
(已知sin10°≈0.17, cos10°≈0.98, tan10°≈0.18, sin15°≈0.26, cos15°≈0.97, tan15°≈0.27.)

25.(本小题满分10分)
小敏的爸爸买了某项体育比赛的一张门票,她和哥哥两人都很想去观看.可门票只有一张,读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2、3、5、9的四张牌给小敏,将数字为4、6、7、8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数,则小敏去;如果和为奇数,则哥哥去.

(1)请用画树形图或列表的方法求小敏去看比赛的概率;
(2)哥哥设计的游戏规则公平吗? 若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
26.(本小题满分10分)
如图,⊙O是Rt△ABC的外接圆,AB为直径,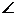 ABC=30°,CD是⊙O的切线,ED⊥AB于F,
ABC=30°,CD是⊙O的切线,ED⊥AB于F,
(1)判断△DCE的形状;
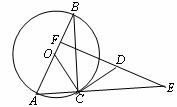
(2)设⊙O的半径为1,且OF=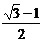 ,求证△DCE≌△OCB.
,求证△DCE≌△OCB.
27.(本小题满分10分)
某人定制了一批地砖,每块地砖(如图(1)所示)是边长为
(1)判断图(2)中四边形EFGH是何形状,并说明理由;
(2)E、F在什么位置时,定制这批地砖所需的材料费用最省?

28.(本小题满分12分)
已知抛物线y=ax2+bx+c的顶点A在x轴上,与y轴的交点为B(0,1),且b=-
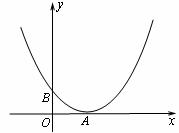
(1) 求抛物线的解析式;
(2) 在抛物线上是否存在一点C,使以BC为直径的圆经过抛物线的顶点A?若不存在说明理由;若存在,求出点C的坐标,并求出此时圆的圆心点P的坐标;
(3) 根据(2)小题的结论,你发现B、P、C三点的横坐标之间、纵坐标之间分别有何关系?
|