
2008年北京市宣武区初三年级二模试卷 数学
一、选择题:
1.-2的绝对值是( )
A.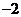 B.
B.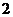 C.
C.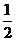 D.
D.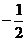
2.近几年北京市教育事业加快发展,据2007年末统计的数据显示,拥有大专以上学历者有约334万人.334万人用科学记数法表示为( )
A.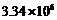 人 B.
人 B.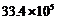 人 C.
人 C.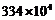 人 D.
人 D.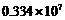 人
人
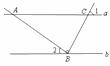
3.如图,直线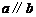 ,点
,点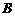 在直线
在直线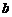 上,且
上,且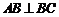 ,
,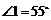 ,则
,则 的度数为( )
的度数为( )
A.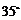 B.
B.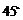 C.
C.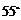 D.
D.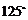
4.下列运算正确的是( )
A.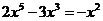 B.
B.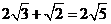
C. D.
D.
5.如图是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲、丙两种品牌彩电该月的销售量之和为( )
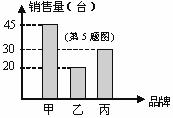
A.50台 B.65台 C.75台 D.95台
6.把代数式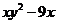 分解因式,结果正确的是( )
分解因式,结果正确的是( )
A.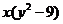 B.
B.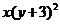 C.
C.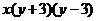 D.
D.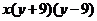
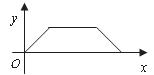
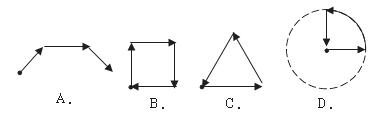
7.如图是韩老师早晨出门散步时,离家的距离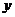 (米)与时间
(米)与时间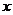 (分钟)之间的函数图象.若用黑点表示韩老师家的位置,则韩老师散步行走的路线可能是( )
(分钟)之间的函数图象.若用黑点表示韩老师家的位置,则韩老师散步行走的路线可能是( )
8.将边长为
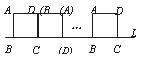
A.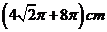 B.
B.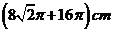
C.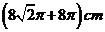 D.
D.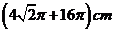
9.函数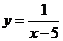 的自变量
的自变量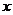 的取值范围是_______________.
的取值范围是_______________.
10.数据12,10,13,8,17,10,21的中位数是 _______________.
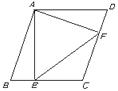
11.如图,在菱形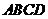 中,
中,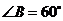 ,点
,点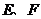 分别从点
分别从点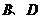 出发以同样的速度沿边
出发以同样的速度沿边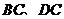 向点
向点 运动.给出以下四个结论:①
运动.给出以下四个结论:①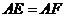 ;②
;②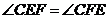 ;③当点
;③当点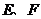 分别为边
分别为边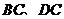 的中点时,
的中点时,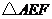 是等边三角形;④当点
是等边三角形;④当点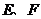 分别为边
分别为边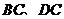 的中点时,
的中点时,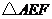 的面积最大.上述结论中正确的序号有 .(把你认为正确的序号都填上)
的面积最大.上述结论中正确的序号有 .(把你认为正确的序号都填上)
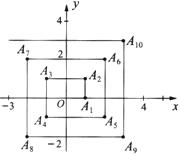
12.如图,已知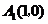 ,
,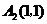 ,
,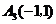 ,
,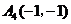 ,
,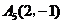 ,则点A2008的坐标为______________.
,则点A2008的坐标为______________.
13.已知a=sin60°,b=cos45°,c=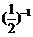 ,d=
,d=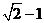 ,从a、b、c、d这4个数中任意选取3个数求和.
,从a、b、c、d这4个数中任意选取3个数求和.
14.用配方法解方程: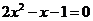 .15.化简:
.15.化简: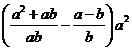 .
.
16.已知 ,
,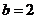 ,求代数式
,求代数式 的值.
的值.
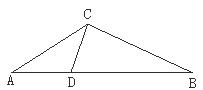
17.已知:如图,在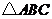 中,
中,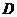 为
为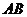 边上一点,
边上一点, 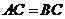 ,
, 求证:
求证: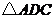 是等腰三角形.
是等腰三角形.
18.如图,已知: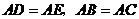 .(1)求证:
.(1)求证: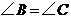 ;(2)若
;(2)若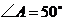 ,问
,问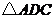 经过怎样的变换能与
经过怎样的变换能与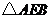 重合?
重合?
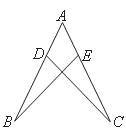
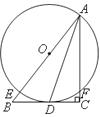
19.如图,已知点 为
为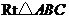 斜边
斜边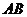 上一点,以
上一点,以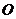 为圆心,
为圆心, 为半径的圆与
为半径的圆与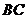 相切于点
相切于点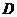 ,与
,与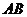 相交于点
相交于点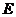 ,与
,与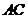 相交于点
相交于点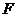 .试判断
.试判断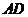 是否平分
是否平分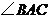 ?并说明理由.
?并说明理由.
20.“石头、剪刀、布”是广为流传的游戏. 游戏时甲、乙双方每次出“石头”、“剪刀”、“布”三种手势中的一种,规定“石头”胜“剪刀”、“剪刀”胜“布”、“布”胜“石头”,同种手势不分胜负.假定甲、乙两人每次都是等可能地出这三种手势,用画树状图或列表的方法分别求出一次游戏中两人出同种手势的概率和甲获胜的概率.(提示:为书写方便,解答时可以用S表示“石头”,用J表示“剪刀”,用B表示“布”)
21. 2008年北京奥运会的比赛部分门票接受公众预订.下表为北京奥运会官方票务网站公布的几种球类比赛的门票价格,某同学一家准备用8000元预订10张下表中比赛项目的门票.
(1)若全部资金用来预订男篮门票和乒乓球门票,问可以订男篮门票和乒乓球门票各多少张?
(2)若在现有资金8000元允许的范围内和总票数不变的前提下,想预订下表中三种球类门票,其中男篮门票数与足球门票数相同,且乒乓球门票的费用不超过男篮门票的费用,求这个家庭能预订三种球类门票各多少张?
比赛项目
票价(元/场)
男篮
1000
足球
800
乒乓球
500
22.如图,已知直线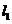 经过点
经过点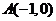 与点
与点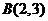 ,另一条直线
,另一条直线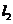 经过点
经过点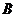 ,且与
,且与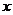 轴相交于点
轴相交于点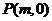 .
.
(1)求直线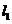 的解析式;
的解析式;
(2)若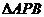 的面积为3,求
的面积为3,求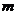 的值.
的值.

23.在四边形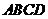 中,对角线
中,对角线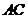 平分
平分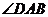 .(1)如图1,当
.(1)如图1,当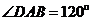 ,
,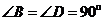 时,求证:
时,求证: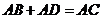 ; (2)如图2,当
; (2)如图2,当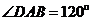 ,
,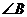 与
与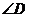 互补时,线段
互补时,线段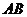 、
、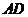 、
、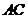 有怎样的数量关系?写出你的猜想,并给予证明;
有怎样的数量关系?写出你的猜想,并给予证明;
(3)如图3,当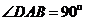 ,
,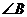 与
与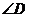 互补时,线段
互补时,线段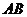 、
、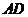 、
、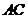 有怎样的数量关系?写出你的猜想,并给予证明.
有怎样的数量关系?写出你的猜想,并给予证明.
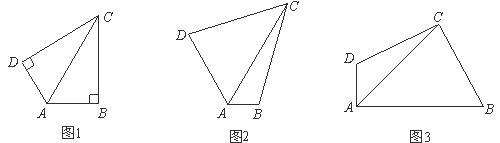
24.已知二次函数图象的对称轴为直线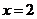 ,经过两点(0,3)和(-1,8),并与
,经过两点(0,3)和(-1,8),并与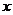 轴的交点为B、C(点C在点B左边),其顶点为点P.(1)求此二次函数的解析式;(2)如果直线
轴的交点为B、C(点C在点B左边),其顶点为点P.(1)求此二次函数的解析式;(2)如果直线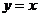 向上或向下平移经过点P,求证:平移后的直线一定经过点B;(3)在(2)的条件下,能否在直线
向上或向下平移经过点P,求证:平移后的直线一定经过点B;(3)在(2)的条件下,能否在直线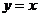 上找一点D,使四边形OPBD是等腰梯形,若能,请求出点D的坐标;若不能,请简要说明你的理由.
上找一点D,使四边形OPBD是等腰梯形,若能,请求出点D的坐标;若不能,请简要说明你的理由.
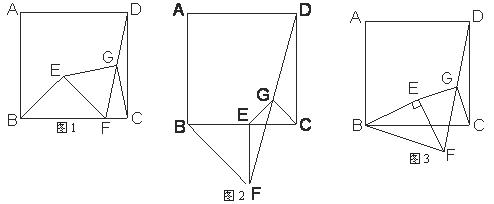
25.已知正方形ABCD和等腰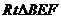 ,BE=EF,∠BEF=
,BE=EF,∠BEF=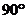 ,按图1放置,使点F在BC上,取DF的中点G,联结EG、CG.
,按图1放置,使点F在BC上,取DF的中点G,联结EG、CG.
(1)探索EG、CG的数量关系和位置关系并证明;
(2)将图1中△BEF绕B点顺时针旋转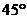 ,再联结DF,取DF中点G(如图2),问(1)中的结论是否仍然成立?证明你的结论;
,再联结DF,取DF中点G(如图2),问(1)中的结论是否仍然成立?证明你的结论;
(3)将图1中△BEF绕B点转动任意角度(旋转角在 到
到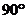 之间),再联结DF,取DF的中点G(如图3),问(1)中的结论是否仍然成立?证明你的结论.
之间),再联结DF,取DF的中点G(如图3),问(1)中的结论是否仍然成立?证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com