
2009年江苏名校高中单独招生考试(三)
数学试卷
(本试卷满分150分,考试时间100分钟)
参考结论:
一元二次方程ax2+bx+c=0的两根为x1,x2,则有
第Ⅰ卷(选择题 共40分)
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中。只有一项是符合题目要求的
1.根据下列表格中x的值与代数式ax2+bx+c的对应值,判断方程ax2+bx+c=0 (a≠0,a,b,c为常数)的一个解x的范围是 ( )
x
6.17
6.18
6.19
6.20
ax2+bx+c
-0.03
-0.01
0.02
0.04
A.6<x<6.17 B.6.17<x<6.18
C.6.18<x<6.19 D.6.19<x<6.20
2.若以连续掷两次骰子分别得到的点数m,n作为点P的横、纵坐标,则点P在直线x+y=5下方的概率为 ( )
A.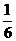 B.
B.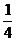 C.
C.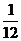 D.
D.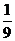
3.在正方形ABCD的边AB,BC,CD,DA上分别任意取点E,F,G,H.这样得到的四边形EFGH中,是正方形的个数有 ( )
A.1 B.
4.一船向正北方向匀速行驶,看见正西方两座相距10海里的灯塔恰好与该船在同一直线上,继续航行半小时后,看见其中一座灯塔在南偏西600方向上,另一灯塔在停偏西750方向上,则该船的速度应该是 ( )
A.10海里/小时 B.10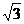 海里/小时
海里/小时
C.5海里/小时 D.5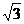 海里/小时
海里/小时
5.如图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么该几何体的侧面积 ( )
A.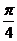 B.
B. C.
C.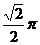 D.
D.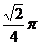
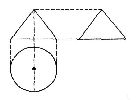
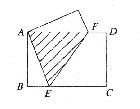
6.矩形纸片ABCD中,AB=3,BC=4,现将纸片折叠压平,使A与C重合,设折痕为EF,则重叠部分△AEF的面积等于 ( )
A.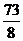 B.
B. 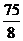 C.
C.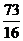 D.
D.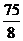
7.张阿姨准备在某商场购买一件衣服、一双鞋和一套化妆品,这三件物品的原价和优惠方式如下表所示:
欲购买的商品
原价(元)
优惠方式
一件衣服
420
每付现金200元,返购物券200元,且付款时可以使用购物券
一双鞋
280
每付现金200元,返购物券200元,但付款时不可以使用购物券
一套化妆品
300
付款时可以使用购物券,但不返购物券
请帮张阿姨分析一下,选择一个最省钱的购买方案.此时,张阿姨购买这三件物品实际所付出的钱的总数为 ( )
A.500元 B.600元 C.700元 D.800元
8.如下图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是 ( )
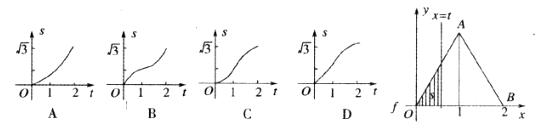
第Ⅱ卷(非选择题共110分)
二、填空题(本大题共10小题。每小题5分,共50分.请把答案填在题中横线上)
9.设A,B两点的坐标分别为(1,1)和(4,3),P点是x轴上的点,则PA+PB的最小值是________.
10.对于自变量x为实数的函数f(x),若存在x0满足f(x0)= x0,则称x0是函数f(x)的一个不动点.若函数f(x)=x2+ax+1没有不动点,则实数a的取值范围是________.
11.对正实数a,b作定义a*b=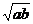 -a+b,若4*x=44,则x的值是________.
-a+b,若4*x=44,则x的值是________.
12.正比例函数与反比例函数图象都经过点(2,b)(b>0),在第一象限内正比例函数图象在反比例函数图象下方的自变量x的取值范围是________.
13.化简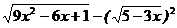 的结果是________.
的结果是________.
14.已知m,n为大于1的正整数,对mn作如下的“分裂”:分解为m个连续奇数的和.如52的“分裂”中最大的数是9.若在m3的“分裂”中最小的数是211,则m=________
15.如图,水平地面上有一个球,现用如下方法测量球的表面积(球的表面积公式S=4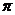 R2)。用锐角∠BAC=600的直角三角板的斜边紧靠球面,P为切点,一条直角边AC紧靠地面,并使三角板与地面垂直,如果测得PA=
R2)。用锐角∠BAC=600的直角三角板的斜边紧靠球面,P为切点,一条直角边AC紧靠地面,并使三角板与地面垂直,如果测得PA=
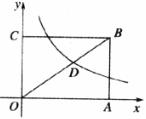
16.如图,已知矩形OABC的面积为 ,它的对角线OB与双曲线
,它的对角线OB与双曲线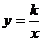 相交于点D,且OB:OD=5:3,则k=________.
相交于点D,且OB:OD=5:3,则k=________.
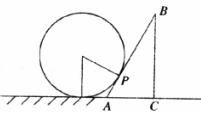
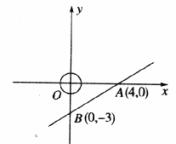
17.直角坐标系中直线AB交x轴,y轴于点A(4,0)与B(0,-3),现有一半径为1的动圆的圆心位于原点处,以每秒1个单位的速度向右作平移运动.则经过_________秒后动圆与直线AB相切.
18.已知直线l1:x-y+2=0;l2:x+y-4=0,两条直线的交点为A,点B在l1,上,点C在l2上,且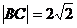 ,当B,C变化时,求过A,B,C三点的动圆形成的区域的面积大小为________.
,当B,C变化时,求过A,B,C三点的动圆形成的区域的面积大小为________.
三、解答题(本大题共5小题,共60分.解答应写出文字说明、证明过程或演算步骤)
19.(本小题满分10分)
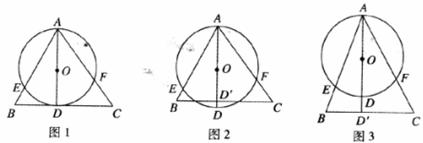
如图1,AD是圆O的直径,BC切圆O于点D,AB,AC与圆O相交于点E,F.
(1)求证:AE?AB=AF?AC;
(2)如果将图1中的直线BC向上平移与圆O相交得图2,或向下平移得图3,此时,AE?AB=AF?AC是否仍成立?若成立,请证明,若不成立,说明理由.
20.(本小题满分12分)
行驶中的汽车,在刹车时由于惯性的作用,要继续往前滑行一段距离才能停下,这段距离称为刹车距离.在某种路面上,某种型号汽车的刹车距离s(米)与汽车车速v(千米/小时)满足下列关系式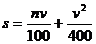 (n为自然数),我们做过两次刹车试验,有关数据如图所示,其中6<s1<8,14<s2<17.
(n为自然数),我们做过两次刹车试验,有关数据如图所示,其中6<s1<8,14<s2<17.
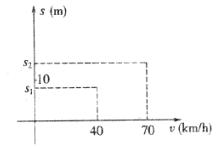
(1)求n的值;
(2)要使刹车距离不超过12.
21.(本小题满分12分)
如图,已知△ABC中,AB=a,点D在AB边上移动(点D不与A,B重合),DE∥BC,交AC于E,连接CD.设S△ABC=S,S△DEC=S1.
(1)当D为AB中点时,求S1:S的值;
(2)若AD=x,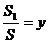 ,求y关于x的函数关系式及自变量x的取值范围;
,求y关于x的函数关系式及自变量x的取值范围;
(3)是否存在点D,使得S1>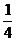 S成立?若存在,求出D点位置;若不存在,请说明理由.
S成立?若存在,求出D点位置;若不存在,请说明理由.

22.(本小题满分12分)
已知函数f(x)=ax2+4x+b,其中a<0,a,b是实数,设关于x的方程f(x)=0的两根为x1,x2,f(x)=x的两实根为
(1)若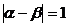 ,求a,b满足的关系式;
,求a,b满足的关系式;
(2)若a,b均为负整数,且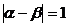 ,求f(x)解析式;
,求f(x)解析式;
(3)试比较(x1+1)( x2+1)与7的大小.
23.(本小题满分14分)
已知y=m2+m+4,若m为整数,在使得y为完全平方数的所有m的值中,设m的最大值为a,最小值为b,次小值为c.(一个数如果是另一个整数的完全平方,那么我们就称这个数为完全平方数.)
(1)求a,b,c的值;
(2)对a,b,c进行如下操作:任取两个求其和再除以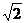 ,同时求其差再除以
,同时求其差再除以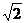 ,剩下的另一个数不变,这样就仍得到三个数.再对所得三个数进行如上操作,问能否经过若干次上述操作,所得三个数的平方和等于2008?证明你的结论.
,剩下的另一个数不变,这样就仍得到三个数.再对所得三个数进行如上操作,问能否经过若干次上述操作,所得三个数的平方和等于2008?证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com