
广东省梅县华侨中学2009届高考最后冲刺测试题
(文科数学)
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中。只有一项是符合题目要求的。
1.已知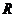 为实数集,
为实数集,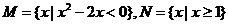 ,则
,则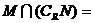 ( ).
( ).
A.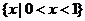 B.
B.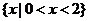 C.
C.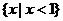 D.
D.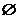
2.设 复数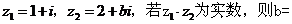 ( )
( )
A.2
B.
3.下列函数中,在区间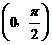 上为增函数且以
上为增函数且以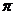 为周期的函数是
为周期的函数是
A.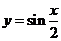 B.
B. 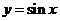 C.
C. 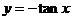 D.
D.
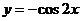
4.给定两个向量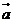 =(3,4)、
=(3,4)、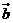 =(2,-1),且(
=(2,-1),且(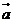 +λ
+λ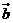 )⊥(
)⊥(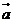 -
-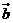 ),则λ=
),则λ=
A、1 B、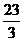 D、
D、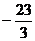
5.条件甲:“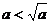 ”是条件乙:“
”是条件乙:“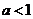 ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.在首项为81,公差为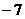 的等差数列
的等差数列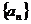 中,最接近零的项是
中,最接近零的项是
A.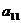 B.
B.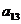 C.
C.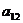 D.
D.
7.函数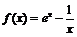 (其中
(其中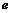 为自然对数的底数)的零点所在的区间是(
)
为自然对数的底数)的零点所在的区间是(
)
A.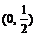 B.
B.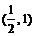 C.
C.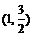 D.
D.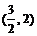
8.已知某个几何体的三视图如下,
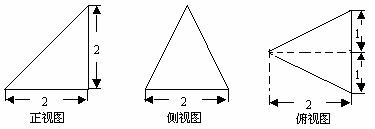
根据图中标出的尺寸(单位:cm),可得这个几何体的体积是
A.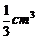 B.
B.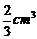 C.
C.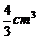 D.
D.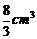
9.在面积为S的△ABC的边AB上任取一点P,则△PBC的面积不小于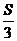 的概率是
的概率是
A.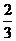 B.
B.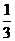 C.
C.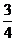 D.
D.
10.若不等式组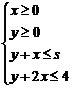 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则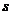 的取值范围是
的取值范围是
A.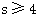 B.
B.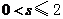 C.
C.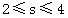 D.
D.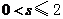 或
或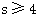
 二、填空题:本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.
二、填空题:本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.
11. 统计某校1000名学生的数学会考成绩,得到样
本频率分布直方图如右图示,规定不低于60分为
及格,不低于80分为优秀,则及格人数是 ;
优秀率为 。
12.与直线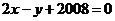 平行且与抛物线
平行且与抛物线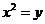 相切的直线方程是
。
相切的直线方程是
。
 13.甲同学家到乙同学家的途中有一公园, 甲到公园的距离与乙到公园的距离都是
13.甲同学家到乙同学家的途中有一公园, 甲到公园的距离与乙到公园的距离都是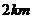 . 如图表示甲从家出发到乙同学家为止经过的路程
. 如图表示甲从家出发到乙同学家为止经过的路程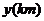 与时间
与时间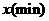 的关系, 其中甲在公园休息的时间是
的关系, 其中甲在公园休息的时间是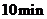 , 那么
, 那么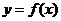 的表达式为 .
的表达式为 .
 14.(坐标系与参数方程选做题) 极坐标系中,曲线
14.(坐标系与参数方程选做题) 极坐标系中,曲线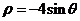 和
和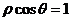 相交于点
相交于点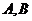 ,则
,则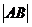 =
;
=
;
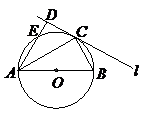
15.(几何证明选讲选做题)如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线 ,则点A到直线
,则点A到直线 的距离AD为 .
的距离AD为 .
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本题满分12分)已知向量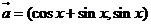 ,
,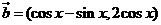 ,
,
设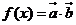 .
.
(1)求函数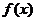 的最小正周期;
的最小正周期;
(2)当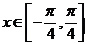 时,求函数
时,求函数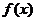 的最大值及最小值.
的最大值及最小值.
17. (本题满分12分)
已知函数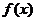 =
=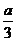 x3+bx2+4cx
x3+bx2+4cx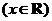 是奇函数,函数
是奇函数,函数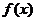 在点
在点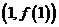 处的切线的斜率为-6, 且当x=2时,函数
处的切线的斜率为-6, 且当x=2时,函数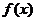 有极值.
有极值.
(I)求b的值;
(II)求函数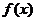 的解析式;
的解析式;
(Ⅲ)求函数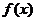 的单调区间.
的单调区间.
18. (本题满分14分) 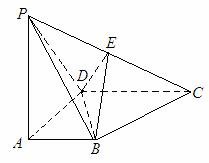 如图所示, 四棱锥P
如图所示, 四棱锥P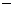 ABCD底面是直角梯形,
ABCD底面是直角梯形, 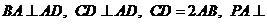 底面ABCD, E为PC的中点, PA=AD=AB=1.
底面ABCD, E为PC的中点, PA=AD=AB=1.
(1)证明:
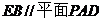 ;
;
(2)证明:
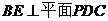 ;
;
(3)求三棱锥B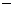 PDC的体积V.
PDC的体积V.
19. (本题满分14分)已知集合 ,在平面直角坐标系中,点
,在平面直角坐标系中,点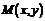 的坐标x∈A,y∈A。计算:
的坐标x∈A,y∈A。计算:
(1)点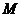 正好在第二象限的概率;
正好在第二象限的概率;
(2)点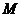 不在x轴上的概率;
不在x轴上的概率;
(3)点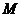 正好落在区域
正好落在区域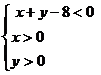 上的概率。
上的概率。
20. (本题满分12分) 已知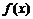 是定义在R上的函数,对于任意的实数a,b,都有
是定义在R上的函数,对于任意的实数a,b,都有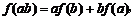
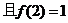 。
。
(Ⅰ)求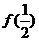 的值;
的值;
(Ⅱ)令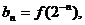 求证:
求证: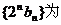 等差数列.
等差数列.
21. (本小题满分14分)
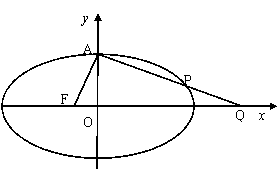 设椭圆C:
设椭圆C: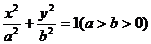 的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且
的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且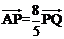 .
.
⑴求椭圆C的离心率;
⑵若过A、Q、F三点的圆恰好与直线l:
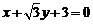 相切,求椭圆C的方程.
相切,求椭圆C的方程.
广东省梅县华侨中学2008届高考最后冲刺测试题
(文科数学)
1-5.ADDCA 6-10:BBC

 9.如图设点P为AB的三等分点,要使△PBC的面积不小于
9.如图设点P为AB的三等分点,要使△PBC的面积不小于 ,则点P只能在
,则点P只能在
AP上选取,由几何概型的概率
公式得所求概率为 .故选A.
.故选A.
10.如图:易得答案选D.
11.由率分布直方图知,及格率= =80%,
=80%,
及格人数=80%×1000=800,优秀率= %.
%.
12.
13.
14.在平面直角坐标系中,曲线 和
和 分别表示圆
分别表示圆 和直线
和直线 ,易知
,易知 =
=
15. C为圆周上一点,AB是直径,所以AC⊥BC,而BC=3,AB=6,得∠BAC=30°,进而得∠B=60°,所以∠DCA=60°,又∠ADC=90°,得∠DAC=30°,

三、解答题
16.解:(1) ………2分
………2分
 ………3分
………3分
 ………5分
………5分
所以函数 的最小正周期
的最小正周期 ………6分
………6分
(2)当 ,
,

 ,
,
∴当 时,
时, 有最大值
有最大值 ;
………10分
;
………10分
当 ,即
,即 时,
时, 有最小值
有最小值 . ………12分
. ………12分
17. 解:(I)由函数 是奇函数,∴
是奇函数,∴ ,
, .
2分
.
2分
(II)由
 x3+4cx,
x3+4cx,
有 ax2+
ax2+ .
.
∴ 解得
解得  6分
6分
故 .
………………………………………………8分
.
………………………………………………8分
?Ⅲ? f(x)=
f(x)= x3-8x,∴
x3-8x,∴ 2x2-8=2(x+2)(x-2).
10分
2x2-8=2(x+2)(x-2).
10分
令 >0得x<-2或x>2 , 令
>0得x<-2或x>2 , 令 <0得-2<x<2.
12分
<0得-2<x<2.
12分
∴函数 的单调增区间为(
的单调增区间为( ,[2,+
,[2,+
 ;单调减区间为[-2,2]. 14分
;单调减区间为[-2,2]. 14分
(或增区间为 ,(2,+
,(2,+
 ;减区间为(-2,2))
;减区间为(-2,2))
18. 证明:(1)取PD中点Q, 连EQ , AQ
, 则 ……………………………………1分
……………………………………1分

 …………………………………………2分
…………………………………………2分
 ………………3分
………………3分
 ………………………5分
………………………5分
 (2)
(2) 
 . ………………………………………10分
. ………………………………………10分
解:(3) …………………………………11分
…………………………………11分
 . ………………………………14分
. ………………………………14分
19. 解:满足条件的 点共有
点共有 个
……………………1分
个
……………………1分
(1)正好在第二象限的点有
 ,
, ,
, ,
, ,
, ,
, ………………3分
………………3分
故点 正好在第二象限的概率P1=
正好在第二象限的概率P1= .
………………4分
.
………………4分
(2)在x轴上的点有 ,
, ,
, ,
, ,
, ,
, ……6分
……6分
故点 不在x轴上的概率P2=1-
不在x轴上的概率P2=1- =
= .
……………………8分
.
……………………8分
(3)在所给区域内的点有 ,
, ,
, ,
, ,
, ,
, ………10分
………10分
故点 在所给区域上的概率
在所给区域上的概率 ……………………11分
……………………11分
答:(1)点 正好在第二象限的概率是
正好在第二象限的概率是 ,(2)点
,(2)点 不在x轴上的概率是
不在x轴上的概率是 ,(3)点
,(3)点 在所给区域上的概率
在所给区域上的概率 …………………14分
…………………14分
20. 解:(1)令 ………2分
………2分
由
(II)
设 ………………………………………………9分
………………………………………………9分
两边同乘以
故数列 等差数列 ……………………………………………12分
等差数列 ……………………………………………12分
A(0,b)知
 设
设 ,
,
得 …2分
…2分
因为点P在椭圆上,所以 …………4分
…………4分
整理得2b2= ,故椭圆的离心率e=
,故椭圆的离心率e= ………6分
………6分
⑵由⑴知 ,
,  于是F(-
于是F(- a,0) Q
a,0) Q ,
,
△AQF的外接圆圆心为( a,0),半径r=
a,0),半径r= |FQ|=a……………………11分
|FQ|=a……………………11分
所以 ,解得a=2,∴c=1,b=
,解得a=2,∴c=1,b= ,所求椭圆方程为
,所求椭圆方程为 ……14分
……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com