精英家教网 >
试题搜索列表 >如果吧六边形换成n边形)n为不小于3的正整数),n边形的外角和是多少?你能类比上面的过程求出来吗?
如果吧六边形换成n边形)n为不小于3的正整数),n边形的外角和是多少?你能类比上面的过程求出来吗?答案解析
科目:czsx
来源:
题型:
(1)用长度相等的100根火柴杆,摆放成一个三角形,使最大边的长度是最小边长度的3倍,求满足此条件的每个三角形的各边所用火柴杆的根数.
(2)现有长为150cm的铁丝,要截成n(n>2)小段,每段的长为不小于1cm的整数.如果其中任意3小段都不能拼成三角形,试求n的最大值,此时有几种方法将该铁丝截成满足条件的n段.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
(1)用长度相等的100根火柴杆,摆放成一个三角形,使最大边的长度是最小边长度的3倍,求满足此条件的每个三角形的各边所用火柴杆的根数.
(2)现有长为150cm的铁丝,要截成n(n>2)小段,每段的长为不小于1cm的整数.如果其中任意3小段都不能拼成三角形,试求n的最大值,此时有几种方法将该铁丝截成满足条件的n段.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
(1)用长度相等的100根火柴杆,摆放成一个三角形,使最大边的长度是最小边长度的3倍,求满足此条件的每个三角形的各边所用火柴杆的根数.
(2)现有长为150cm的铁丝,要截成n(n>2)小段,每段的长为不小于lcm的整数.如果其中任意3小段都不能拼成三角形,试求n的最大值,此时有几种方法将该铁丝截成满足条件的n段.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
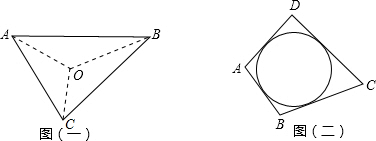
阅读材料:如图(一),△ABC的周长为l,内切圆O的半径为r,连接OA、OB、OC,△ABC被划分为三个小三角形,用S
△ABC表示△ABC的面积.
∵S
△ABC=S
△OAB+S
△OBC+S
△OCA又∵S
△OAB=
AB•r,S
△OBC=
BC•r,S
△OCA=
CA•r
∴S
△ABC=
AB•r+
BC•r+
CA•r=
l•r(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a
1、a
2、a
3、…、a
n,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
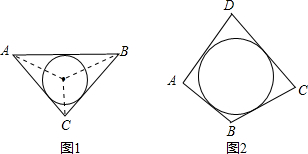
阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S
△OAB+S
△OBC+S
△OCA又∵
S△OAB=AB•r,
S△OBC=BC•r,
S△OCA=CA•r∴
S=AB•r+BC•r+CA•r=l•r∴
r=解决问题:
(1)利用探究的结论,计算边长分别为5,12,13的三角形内切圆半径;
(2)若四边形ABCD存在内切圆(与各边都相切的圆),如图2且面积为S,各边长分别为a,b,c,d,试推导四边形的内切圆半径公式;
(3)若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a
1,a
2,a
3,…,a
n,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
科目:czsx
来源:
题型:
9、已知一组数据2,15,15,15,35,25.把其中的数据2换成另外一个数,下列数据不会改变的是( )
查看答案和解析>>
科目:czsx
来源:2011届河北省廊坊市安次区初三第一次模拟考试数学试题
题型:解答题
查看答案和解析>>
科目:czsx
来源:2012年沪科版初中数学九年级下26.6三角形的内切圆练习卷(解析版)
题型:解答题
阅读材料:如图(1),△ABC的周长为L,内切圆O的半径为r,连结OA,OB,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积.
∵S△ABC =S△OAB +S△OBC +S△OCA
又∵S△OAB = AB·r,S△OBC =
AB·r,S△OBC = BC·r,S△OCA =
BC·r,S△OCA = AC·r
AC·r
∴S△ABC = AB·r+
AB·r+ BC·r+
BC·r+ CA·r
CA·r
= L·r(可作为三角形内切圆半径公式)
L·r(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5,12,13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(2)且面积为S,各边长分别为a,b,c,d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1,a2,a3,…an,合理猜想其内切圆半径公式(不需说明理由).

查看答案和解析>>
科目:czsx
来源:第5章《中心对称图形(二)》中考题集(45):5.5 直线与圆的位置关系(解析版)
题型:解答题
阅读材料:如图(一),△ABC的周长为l,内切圆O的半径为r,连接OA、OB、OC,△ABC被划分为三个小三角形,用S
△ABC表示△ABC的面积.

∵S
△ABC=S
△OAB+S
△OBC+S
△OCA又∵S
△OAB=

AB•r,S
△OBC=

BC•r,S
△OCA=

CA•r
∴S
△ABC=

AB•r+

BC•r+

CA•r=

l•r(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a
1、a
2、a
3、…、a
n,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
科目:czsx
来源:第28章《圆》中考题集(58):28.2 与圆有关的位置关系(解析版)
题型:解答题
阅读材料:如图(一),△ABC的周长为l,内切圆O的半径为r,连接OA、OB、OC,△ABC被划分为三个小三角形,用S
△ABC表示△ABC的面积.

∵S
△ABC=S
△OAB+S
△OBC+S
△OCA又∵S
△OAB=

AB•r,S
△OBC=

BC•r,S
△OCA=

CA•r
∴S
△ABC=

AB•r+

BC•r+

CA•r=

l•r(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a
1、a
2、a
3、…、a
n,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
科目:czsx
来源:第3章《圆》中考题集(52):3.5 直线和圆的位置关系(解析版)
题型:解答题
阅读材料:如图(一),△ABC的周长为l,内切圆O的半径为r,连接OA、OB、OC,△ABC被划分为三个小三角形,用S
△ABC表示△ABC的面积.

∵S
△ABC=S
△OAB+S
△OBC+S
△OCA又∵S
△OAB=

AB•r,S
△OBC=

BC•r,S
△OCA=

CA•r
∴S
△ABC=

AB•r+

BC•r+

CA•r=

l•r(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a
1、a
2、a
3、…、a
n,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
科目:czsx
来源:第24章《圆(下)》中考题集(24):24.2 圆的切线(解析版)
题型:解答题
阅读材料:如图(一),△ABC的周长为l,内切圆O的半径为r,连接OA、OB、OC,△ABC被划分为三个小三角形,用S
△ABC表示△ABC的面积.

∵S
△ABC=S
△OAB+S
△OBC+S
△OCA又∵S
△OAB=

AB•r,S
△OBC=

BC•r,S
△OCA=

CA•r
∴S
△ABC=

AB•r+

BC•r+

CA•r=

l•r(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a
1、a
2、a
3、…、a
n,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
科目:czsx
来源:第3章《圆》中考题集(50):3.2 点、直线与圆的位置关系,圆的切线(解析版)
题型:解答题
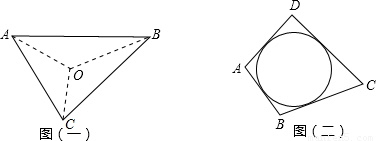
阅读材料:如图(一),△ABC的周长为l,内切圆O的半径为r,连接OA、OB、OC,△ABC被划分为三个小三角形,用S
△ABC表示△ABC的面积.
∵S
△ABC=S
△OAB+S
△OBC+S
△OCA又∵S
△OAB=

AB•r,S
△OBC=

BC•r,S
△OCA=

CA•r
∴S
△ABC=

AB•r+

BC•r+

CA•r=

l•r(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a
1、a
2、a
3、…、a
n,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
科目:czsx
来源:2006年江苏省淮安市中考数学试卷(课标卷)(解析版)
题型:解答题
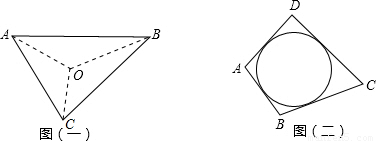
(2006•淮安)阅读材料:如图(一),△ABC的周长为l,内切圆O的半径为r,连接OA、OB、OC,△ABC被划分为三个小三角形,用S
△ABC表示△ABC的面积.
∵S
△ABC=S
△OAB+S
△OBC+S
△OCA又∵S
△OAB=

AB•r,S
△OBC=

BC•r,S
△OCA=

CA•r
∴S
△ABC=

AB•r+

BC•r+

CA•r=

l•r(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a
1、a
2、a
3、…、a
n,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
科目:czsx
来源:数学教研室
题型:022
在n边形(n为不小于3的自然数)内取一个点,与n边形的每条边可以组成_______个三角形.
查看答案和解析>>
科目:czsx
来源:2010年河北省廊坊市安次区中考数学一模试卷(解析版)
题型:解答题
(2010•安次区一模)阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S
△OAB+S
△OBC+S
△OCA又∵
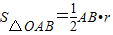
,
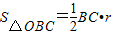
,
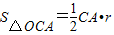
∴
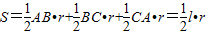
∴
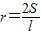
解决问题:
(1)利用探究的结论,计算边长分别为5,12,13的三角形内切圆半径;
(2)若四边形ABCD存在内切圆(与各边都相切的圆),如图2且面积为S,各边长分别为a,b,c,d,试推导四边形的内切圆半径公式;
(3)若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a
1,a
2,a
3,…,a
n,合理猜想其内切圆半径公式(不需说明理由).
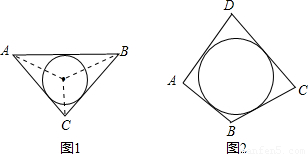
查看答案和解析>>
科目:czsx
来源:第35章《圆(二)》中考题集(28):35.4 切线的判定(解析版)
题型:解答题
阅读材料:如图(一),△ABC的周长为l,内切圆O的半径为r,连接OA、OB、OC,△ABC被划分为三个小三角形,用S
△ABC表示△ABC的面积.
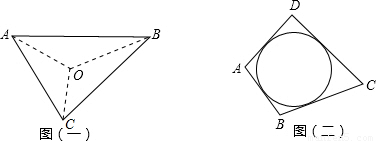
∵S
△ABC=S
△OAB+S
△OBC+S
△OCA又∵S
△OAB=

AB•r,S
△OBC=

BC•r,S
△OCA=

CA•r
∴S
△ABC=

AB•r+

BC•r+

CA•r=

l•r(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a
1、a
2、a
3、…、a
n,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
科目:czsx
来源:第26章《圆》中考题集(63):26.6 三角形的内切圆(解析版)
题型:解答题
阅读材料:如图(一),△ABC的周长为l,内切圆O的半径为r,连接OA、OB、OC,△ABC被划分为三个小三角形,用S
△ABC表示△ABC的面积.

∵S
△ABC=S
△OAB+S
△OBC+S
△OCA又∵S
△OAB=

AB•r,S
△OBC=

BC•r,S
△OCA=

CA•r
∴S
△ABC=

AB•r+

BC•r+

CA•r=

l•r(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a
1、a
2、a
3、…、a
n,合理猜想其内切圆半径公式(不需说明理由).
查看答案和解析>>
科目:czsx
来源:河北省模拟题
题型:解答题
阅读材料:如图1所示,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系,连接OA,OB,OC。
∵S=S
△OAB+S
△OBC+S
△OCA
又∵

,

,

∴

∴

解决问题:
(1)利用探究的结论,计算边长分别为5,12,13的三角形内切圆半径;
(2)若四边形ABCD存在内切圆(与各边都相切的圆),如图2且面积为S,各边长分别为a,b,c,d,试推导四边形的内切圆半径公式;
(3)若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a
1,a
2,a
3,…,a
n,合理猜想其内切圆半径公式(不需说明理由)。

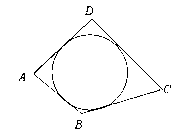
图1 图2
查看答案和解析>>


 阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S△OAB+S△OBC+S△OCA
阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S△OAB+S△OBC+S△OCA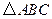 的周长为
的周长为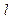 ,面积为S,内切圆
,面积为S,内切圆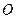 的半径为
的半径为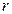 ,探究
,探究 与S、
与S、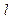 之间的关系.连结
之间的关系.连结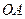 ,
,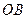 ,
,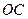
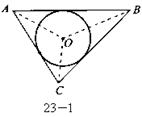
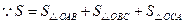
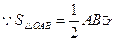 ,
,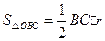 ,
,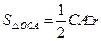
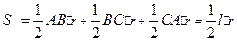
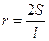
 :
: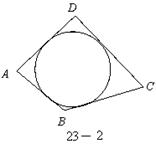
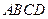 存在内切圆(与各边都相切的圆),如图23—2且面积为
存在内切圆(与各边都相切的圆),如图23—2且面积为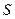 ,各边长分别为
,各边长分别为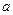 ,
,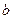 ,
,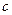 ,
,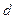 ,试推导四边形的内切圆半径公式;
,试推导四边形的内切圆半径公式;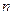 边形(
边形(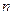 为不小于3的整数)存在内切圆,且面积为
为不小于3的整数)存在内切圆,且面积为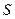 ,各边长分别为
,各边长分别为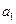 ,
, ,
,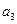 ,
,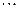 ,
,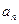 ,合理猜想其内切圆半径公式(不需说明理由).
,合理猜想其内切圆半径公式(不需说明理由). AB·r,S△OBC =
AB·r,S△OBC = BC·r,S△OCA =
BC·r,S△OCA = AC·r
AC·r AB·r+
AB·r+ BC·r+
BC·r+ CA·r
CA·r L·r(可作为三角形内切圆半径公式)
L·r(可作为三角形内切圆半径公式)

 AB•r,S△OBC=
AB•r,S△OBC= BC•r,S△OCA=
BC•r,S△OCA= CA•r
CA•r AB•r+
AB•r+ BC•r+
BC•r+ CA•r=
CA•r= l•r(可作为三角形内切圆半径公式)
l•r(可作为三角形内切圆半径公式)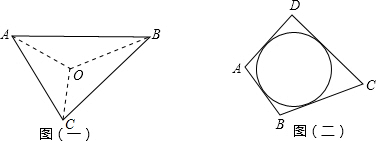
 AB•r,S△OBC=
AB•r,S△OBC= BC•r,S△OCA=
BC•r,S△OCA= CA•r
CA•r AB•r+
AB•r+ BC•r+
BC•r+ CA•r=
CA•r= l•r(可作为三角形内切圆半径公式)
l•r(可作为三角形内切圆半径公式)
 AB•r,S△OBC=
AB•r,S△OBC= BC•r,S△OCA=
BC•r,S△OCA= CA•r
CA•r AB•r+
AB•r+ BC•r+
BC•r+ CA•r=
CA•r= l•r(可作为三角形内切圆半径公式)
l•r(可作为三角形内切圆半径公式)
 AB•r,S△OBC=
AB•r,S△OBC= BC•r,S△OCA=
BC•r,S△OCA= CA•r
CA•r AB•r+
AB•r+ BC•r+
BC•r+ CA•r=
CA•r= l•r(可作为三角形内切圆半径公式)
l•r(可作为三角形内切圆半径公式)
 AB•r,S△OBC=
AB•r,S△OBC= BC•r,S△OCA=
BC•r,S△OCA= CA•r
CA•r AB•r+
AB•r+ BC•r+
BC•r+ CA•r=
CA•r= l•r(可作为三角形内切圆半径公式)
l•r(可作为三角形内切圆半径公式)
 AB•r,S△OBC=
AB•r,S△OBC= BC•r,S△OCA=
BC•r,S△OCA= CA•r
CA•r AB•r+
AB•r+ BC•r+
BC•r+ CA•r=
CA•r= l•r(可作为三角形内切圆半径公式)
l•r(可作为三角形内切圆半径公式)
 AB•r,S△OBC=
AB•r,S△OBC= BC•r,S△OCA=
BC•r,S△OCA= CA•r
CA•r AB•r+
AB•r+ BC•r+
BC•r+ CA•r=
CA•r= l•r(可作为三角形内切圆半径公式)
l•r(可作为三角形内切圆半径公式)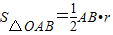 ,
,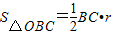 ,
,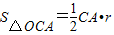
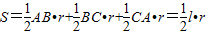
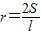


 AB•r,S△OBC=
AB•r,S△OBC= BC•r,S△OCA=
BC•r,S△OCA= CA•r
CA•r AB•r+
AB•r+ BC•r+
BC•r+ CA•r=
CA•r= l•r(可作为三角形内切圆半径公式)
l•r(可作为三角形内切圆半径公式)
 AB•r,S△OBC=
AB•r,S△OBC= BC•r,S△OCA=
BC•r,S△OCA= CA•r
CA•r AB•r+
AB•r+ BC•r+
BC•r+ CA•r=
CA•r= l•r(可作为三角形内切圆半径公式)
l•r(可作为三角形内切圆半径公式) ,
, ,
,



