
科目:gzsx 来源:2013届辽宁省庄河市高二开学初考试理科数学试卷 题型:解答题
如图,已知椭圆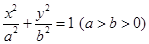 的离心率为
的离心率为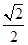 ,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为
,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
(1)求椭圆和双曲线的标准方程
(2)设直线PF1、PF2的斜率分别为k1、k2,证明:k1·k2=1
(3)是否存在常数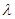 ,使得|AB|+|CD|=
,使得|AB|+|CD|=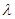 |AB|·|CD|恒成立?
|AB|·|CD|恒成立?
若存在,求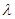 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
科目:gzsx 来源:2013届度黑龙江龙东地区第一学期高二期末理科数学试卷 题型:解答题
如图,已知椭圆 的离心率为
的离心率为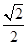 ,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为
,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为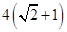 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
(Ⅰ)求椭圆和双曲线的标准方程
(Ⅱ)设直线PF1、PF2的斜率分别为k1、k2,证明:k1·k2=1
(Ⅲ)是否存在常数 ,使得|AB|+|CD|=
,使得|AB|+|CD|= |AB|·|CD|恒成立?若存在,求
|AB|·|CD|恒成立?若存在,求 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
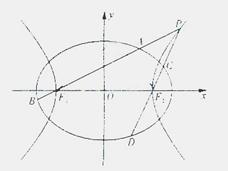
科目:gzsx 来源:2013届四川省巴中市四县中高二上学期期末考试理科数学 题型:解答题
((本题14分)如图4,已知椭圆 的离心率为
的离心率为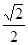 ,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4
,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线PF1、PF2的斜率分别为 ;
;
(Ⅲ)是否存在常数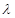 ,使得
,使得 恒成立?若存在,求
恒成立?若存在,求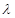 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。

科目:gzsx 来源:黑龙江省龙东地区2011-2012学年度高二上学期高中教学联合体期末数学理科试卷 题型:044
如图,已知椭圆![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为4(
,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为4(![]() +1).一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D.
+1).一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D.
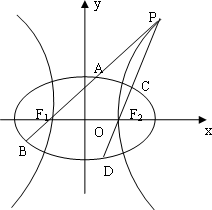
(Ⅰ)求椭圆和双曲线的标准方程
(Ⅱ)设直线PF1、PF2的斜率分别为k1、k2,证明:k1·k2=1
(Ⅲ)是否存在常数λ,使得|AB|+|CD|=λ|AB|·|CD|恒成立?若存在,求λ的值,若不存在,请说明理由.
科目:gzsx 来源:黑龙江龙东地区2011-2012学年高二上学期高中教学联合体期末考试数学理科试题 题型:044
如图,已知椭圆![]() 的离心率为
的离心率为![]() ,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为
,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为![]() .一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D.
.一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D.

(Ⅰ)求椭圆和双曲线的标准方程
(Ⅱ)设直线PF1、PF2的斜率分别为k1、k2,证明:k1·k2=1
(Ⅲ)是否存在常数λ,使得|AB|+|CD|=λ|AB|·|CD|恒成立?
若存在,求λ的值,若不存在,请说明理由.
科目:gzsx 来源:2011-2012学年安徽省高三10月月考理科数学试卷 题型:填空题
设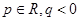 ,当函数
,当函数 的零点多于1个时,
的零点多于1个时,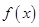 在以其最小零点与最大零点为端点的闭区间上的最大值为_____________.
在以其最小零点与最大零点为端点的闭区间上的最大值为_____________.
科目:gzsx 来源:2012-2013学年安徽省安庆市潜山中学高三(上)第三次月考数学试卷(理科)(解析版) 题型:填空题
科目:gzsx 来源: 题型:
(08年重庆一中一模文)为了解某次测验成绩,在全年级随机地抽查了100名学生的成绩,得到频率分布直方图(如右图),由于某种原因使部分数据丢失,但知道后5组的学生人数成等比数列,设90分以下人数为![]() ,最大频率为
,最大频率为![]() ,则
,则![]() 的值分别为( )
的值分别为( )
A.69, 0.53 B.38, 0.32
C.69, 5.3 D.38, 3.2

科目:gzsx 来源:安徽省蚌埠二中2011-2012学年高三上学期10月考(数学理) 题型:填空题
设 ,当函数
,当函数 的零点多于1个时,
的零点多于1个时, 在以其最小零点与最大零点为端点的闭区间上的最大值为_____________.
在以其最小零点与最大零点为端点的闭区间上的最大值为_____________.
科目:gzsx 来源: 题型:填空题
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
| 4 |
| 3-5cosθ |
A、焦点到准线距离为
| ||
B、焦点到准线距离为
| ||
C、焦点到准线距离为
| ||
D、焦点到准线距离为
|
科目:gzsx 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
| ||
|
| ||
|
科目:gzsx 来源: 题型:
科目:gzsx 来源:2010年江西省吉安市高一下学期期末考试数学卷 题型:解答题
(本小题满分12分)
一袋中装有分别标记着1,2,3,4,5数字的5个球,
(1)从袋中一次取出2个球,试求2个球中最大数字为4的概率;
(2)从袋中每次取出一个球,取出后放回,连续取2次,试求取出的2个球中最大数字为5的概率。