
科目:gzsx 来源: 题型:
(本题满分12分)
在直角坐标系![]() 中,点
中,点![]() 到两点
到两点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,设点
,设点![]() 的轨迹为
的轨迹为![]() 。
。
(1)求曲线![]() 的方程; Ks5u
的方程; Ks5u
(2)过点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() ,以线段
,以线段![]() 为直径的圆过能否过坐标原点,若能,求直线
为直径的圆过能否过坐标原点,若能,求直线![]() 的斜率,若不能说明理由.
的斜率,若不能说明理由.
科目:gzsx 来源:2012-2013学年重庆市高三上学期二轮复习定时练习(一)文科数学试卷(解析版) 题型:解答题
设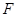 是椭圆
是椭圆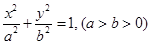 的左焦点,直线
的左焦点,直线 方程为
方程为 ,直线
,直线 与
与 轴交于
轴交于 点,
点, 、
、 分别为椭圆的左右顶点,已知
分别为椭圆的左右顶点,已知 ,且
,且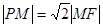 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点 且斜率为
且斜率为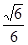 的直线交椭圆于
的直线交椭圆于 、
、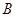 两点,求三角形
两点,求三角形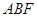 面积.
面积.
科目:gzsx 来源:2014届河南安阳一中高二第一次阶段测试理科数学试卷(解析版) 题型:解答题
已知椭圆方程为 ,
, 、
、 为其左右焦点,点
为其左右焦点,点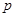 为椭圆上一点,且
为椭圆上一点,且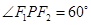 ,
,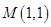 .
.
(1)求 的面积. (2)直线
的面积. (2)直线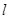 过点
过点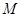 与椭圆交于
与椭圆交于 、
、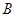 两点,若
两点,若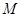 为弦
为弦
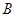 的中点,求
的中点,求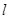 的方程.
的方程.
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| θ |
| 2 |
| DF |
| BF |
科目:gzsx 来源:2014届山东省莱芜市高二上学期期末考试文数试卷(解析版) 题型:解答题
(本小题满分12分)
抛物线顶点在坐标原点,焦点与椭圆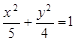 的右焦点
的右焦点 重合,过点
重合,过点 斜率为
斜率为 的直线与抛物线交于
的直线与抛物线交于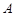 ,
, 两点.
两点.

(Ⅰ)求抛物线的方程;
(Ⅱ)求△ 的面积.
的面积.
科目:gzsx 来源: 题型:
(08年长沙一中一模理)已知椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 与以原点为圆心、椭圆
与以原点为圆心、椭圆![]() 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 过点
过点![]() 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线![]() 垂直
垂直![]() 于点P,线段
于点P,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点M,求动点M的轨迹
于点M,求动点M的轨迹![]() 的方程;
的方程;
(3)过椭圆![]() 的焦点
的焦点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于A、B两点,当
交于A、B两点,当![]() 的斜率为
的斜率为![]() 时,直线
时,直线![]() 上是否存在点M,使
上是否存在点M,使![]() 若存在,求出M的坐标,若不存在,说明理由.
若存在,求出M的坐标,若不存在,说明理由.
科目:gzsx 来源: 题型:
已知椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 与以原点为圆心、椭圆
与以原点为圆心、椭圆![]() 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设椭圆![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 过点
过点![]() 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线![]() 垂直
垂直![]() 于点P,线段
于点P,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点M,求动点M的轨迹
于点M,求动点M的轨迹![]() 的方程;
的方程;
(Ⅲ)过椭圆![]() 的焦点
的焦点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于A、B两点,当
交于A、B两点,当![]() 的斜率为
的斜率为![]() 时,直线
时,直线![]() 上是否存在点M,使
上是否存在点M,使![]() 若存在,求出M的坐标,若不存在,说明理由
若存在,求出M的坐标,若不存在,说明理由
科目:gzsx 来源:2014届黑龙江省高二上学期期末文科数学试卷(解析版) 题型:选择题
直线 与椭圆
与椭圆 交于
交于 两点,以线段
两点,以线段 为直径的圆过椭圆的右焦点,则椭圆
为直径的圆过椭圆的右焦点,则椭圆 的离心率为( )
的离心率为( )
A. B.
B.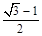 C.
C. D.
D.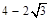
科目:gzsx 来源:2012-2013学年江西南昌10所省高三第二次模拟文科数学试卷(七)(解析版) 题型:解答题
已知椭圆 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为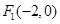 ,
,
 ,点
,点 在椭圆
在椭圆 上,过点
上,过点 的直线
的直线 与抛物线
与抛物线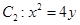 交于
交于 两点,抛物线
两点,抛物线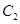 在点
在点 处的切线分别为
处的切线分别为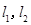 ,且
,且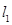 与
与 交于点
交于点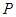 .
.
(1) 求椭圆 的方程;
的方程;
(2) 是否存在满足 的点
的点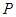 ? 若存在,指出这样的点
? 若存在,指出这样的点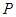 有几个(不必求出点
有几个(不必求出点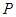 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
科目:gzsx 来源:2014届浙江宁波万里国际学校高二下学期期中考试文数学试卷(解析版) 题型:解答题
已知椭圆C:
 的短轴长等于焦距,椭圆C上的点到右焦点
的短轴长等于焦距,椭圆C上的点到右焦点 的最短距离为
的最短距离为 .
.
(1)求椭圆C的方程;
(2)过点 且斜率为
且斜率为 (
( >0)的直线
>0)的直线 与C交于
与C交于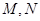 两点,
两点, 是点
是点 关于
关于 轴的对称点,证明:
轴的对称点,证明: 三点共线.
三点共线.
科目:gzsx 来源:2014届广东省汕头市高二下学期期中理科数学试卷(解析版) 题型:解答题
已知椭圆 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为 ,
,
 ,点
,点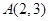 在椭圆
在椭圆 上,过点
上,过点 的直线
的直线 与抛物线
与抛物线 交于
交于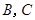 两点,抛物线
两点,抛物线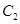 在点
在点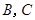 处的切线分别为
处的切线分别为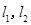 ,且
,且 与
与 交于点
交于点 .
.
(1) 求椭圆 的方程;
的方程;
(2) 是否存在满足 的点
的点 ? 若存在,指出这样的点
? 若存在,指出这样的点 有几个(不必求出点
有几个(不必求出点 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
科目:gzsx 来源:2012-2013学年广东省广州市高三3月毕业班综合测试(一)理科数学试卷(解析版) 题型:解答题
(本小题满分14分)
已知椭圆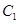 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为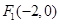 ,
,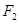
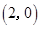 ,点
,点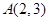 在椭圆
在椭圆 上,过点
上,过点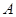 的直线
的直线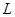 与抛物线
与抛物线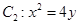 交于
交于 两点,抛物线
两点,抛物线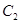 在点
在点 处的切线分别为
处的切线分别为 ,且
,且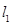 与
与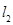 交于点
交于点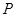 .
.
(1) 求椭圆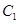 的方程;
的方程;
(2) 是否存在满足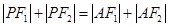 的点
的点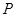 ? 若存在,指出这样的点
? 若存在,指出这样的点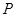 有几个(不必求出点
有几个(不必求出点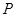 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.
科目:gzsx 来源:贵州省五校联盟2012届高三第四次联考数学理科试题 题型:022
已知点F和直线l分别是椭圆![]() 的右焦点和右准线.过点F作斜率为
的右焦点和右准线.过点F作斜率为![]() 的直线,该直线与l交于点A,与椭圆的一个交点是B,且
的直线,该直线与l交于点A,与椭圆的一个交点是B,且![]() =2
=2![]() .则椭圆的离心率e=________.
.则椭圆的离心率e=________.
科目:gzsx 来源:贵州省五校联盟2012届高三第四次联考数学文科试题 题型:022
已知点F和直线l分别是椭圆![]() 的右焦点和右准线.过点F作斜率为
的右焦点和右准线.过点F作斜率为![]() 的直线,该直线与l交于点A,与椭圆的一个交点是B,且
的直线,该直线与l交于点A,与椭圆的一个交点是B,且![]() =2
=2![]() .则椭圆的离心率e=________.
.则椭圆的离心率e=________.
科目:gzsx 来源:2011年四川省成都七中高考数学模拟最后一卷(理科)(解析版) 题型:解答题
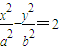 (a>0,b>0)的左右焦点为F1,F2,其上一点P,若∠F1PF2=θ,
(a>0,b>0)的左右焦点为F1,F2,其上一点P,若∠F1PF2=θ, ;
;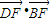 的值.
的值.科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
科目:gzsx 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练19练习卷(解析版) 题型:选择题
已知双曲线 -
- =1(a>0,b>0),过其右焦点F且垂直于实轴的直线与双曲线交于M,N两点,O为坐标原点.若OM⊥ON,则双曲线的离心率为( )
=1(a>0,b>0),过其右焦点F且垂直于实轴的直线与双曲线交于M,N两点,O为坐标原点.若OM⊥ON,则双曲线的离心率为( )
(A) (B)
(B)
(C) (D)
(D)
科目:gzsx 来源:2012-2013学年甘肃省高三上学期第一次检测理科数学试卷(解析版) 题型:选择题
设直线L过双曲线C的一个焦点,且与C的一条对称轴垂直,L与C交于A ,B两点, 为C的实轴长的2倍,则C的离心率为( )
为C的实轴长的2倍,则C的离心率为( )
A. B.
B.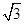 C.2 D.3
C.2 D.3
科目:gzsx 来源:2011年高考试题数学(全国卷新课标)解析版 题型:选择题
设直线L过双曲线C的一个焦点,且与C的一条对称轴垂直,L与C交于A ,B两点, 为C的实轴长的2倍,则C的离心率为
为C的实轴长的2倍,则C的离心率为
(A) (B)
(B) (C)2
(D)3
(C)2
(D)3