(a+b)(a-b)(a^4+a2b2+b^4)答案解析
科目:czsx
来源:
题型:
25、已知A=a3+3a2b2+2b2+3b,B=a3-a2b2+b2+3b.A与B的关系是( )
查看答案和解析>>
科目:czsx
来源:
题型:
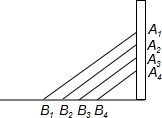
斜拉桥是利用一组组钢索,把桥面重力传递到耸立在两侧高塔上的桥梁,它不需要建造桥墩,(如图所示),B
2、B
3、B
4是B
1到高塔底端的四等分点,其中A
1B
1、A
2B
2、A
3B
3、A
4B
4是斜拉桥上互相平行的钢索,若最长的钢索A
1B
1=80m,最短的钢索A
4B
4=20m,那么钢索A
2B
2=
m,A
3B
3=
m.
查看答案和解析>>
科目:czsx
来源:
题型:
若点P的坐标(a,b)满足a
2b
2+a
2+b
2+10ab+16=0,则点P的坐标为
(2,-2)或(-2,2)
(2,-2)或(-2,2)
.
查看答案和解析>>
科目:czsx
来源:
题型:
下列四个算式:
①(-3x)4÷(-9x3)=-9x
②x(-x3)2n+1÷(-x3)=-x6n
③a7b3÷(a2b2)=a3b
④-15a5b3÷5a3b2=-3a2b
其中计算不正确的是( )
查看答案和解析>>
科目:czsx
来源:
题型:
我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积.用现代式子表示即为:
s=…①(其中a、b、c为三角形的三边长,s为面积).
而另一个文明古国古希腊也有求三角形面积的海伦公式:
s=
…②(其中p=
.)
(1)若已知三角形的三边长分别为5,7,8,试分别运用公式①和公式②,计算该三角形的面积s;
(2)你能否由公式①推导出公式②?请试试.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:△ABC中,AB=a.
如图(1),若A
1、B
1分别是CA、CB的中点,则A
1B
1=
;
如图(2),若A
1、A
2、B
1、B
2分别是CA、CB的三等分点,则A
1B
1+A
2B
2=
a=a;
如图(3),若A
1、A
2、A
3、B
1、B
2、B
3分别是CA、CB的四等分点,则A
1B
1+A
2B
2+A
3B
3=
a=
a;
如图(4),若A
1、A
2、A
3、…A
9、B
1、B
2、B
3、…B
9分别是CA、CB的十等分点,则A
1B
1+A
2B
2+A
3B
3+…+A
9B
9=
.
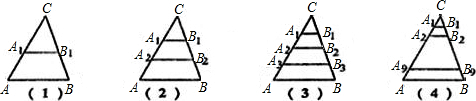
查看答案和解析>>
科目:czsx
来源:
题型:
有一道题:“先化简再求值:(a+b)
2-(a+b)(a-2b)-(a
2b
2+
b
3)÷
b,其中a=-2009,b=2008”,小明做题时把“a=-2009”错抄成了“a=2009”,但他的计算结果也是正确的,请你通过计算解释这是怎么回事?
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABA
1中,∠B=20°,AB=A
1B,在A
1B上取一点B
1,延长AA
1到A
2,使A
1A
2=A
1B
1,在A
2B
1上取一点B
2,延长到A
1A
2到A
3,使A
2A
3=A
2B
2;…按此方法进行下去,∠A
n-1A
nB
n-1的度数为
.
查看答案和解析>>
科目:czsx
来源:
题型:
已知两个整式的差是 c2 d2-a2 b2,如果其中一个整式是 a2b2+c2d2-2abcd,求另一个整式.
查看答案和解析>>
科目:czsx
来源:
题型:
观察如图所包含规律(图中三角形均是直角三角形,且一条直角边始终为1,四边形均为正方形.S
1,S
2,S
3,…S
n依次表示正方形的面积,每个正方形边长与它左边相邻的直角三角形斜边相等),再回答下列问题.
(1)填表:
| 直角边 |
A1B1 |
A2B2 |
A3B3 |
A4B4 |
… |
AnBn |
| 长度 |
1 |
|
|
|
… |
|
(2)当s
1+s
2+s
3+s
4+…+s
n=465时,求n.

查看答案和解析>>
科目:czsx
来源:
题型:

11、挪威数学家阿贝尔,年轻时就利用阶梯形,发现了一个重要的恒等式--阿贝尔公式:如图是一个简单的阶梯形,可用两种方法,每一种把图形分割成为两个矩形.利用它们之间的面积关系,可以得到:a
1b
1+a
2b
2=( )
查看答案和解析>>
科目:czsx
来源:
题型:
对于每个自然数n,抛物线
y=x2-x+与x轴交于A
n、B
n两点,以|A
nB
n|表示该两点间的距离,则|A
1B
1|+|A
2B
2|+…+|A
2011B
2011|的值为( )
查看答案和解析>>
科目:czsx
来源:
题型:
用一段长为10米的篱笆,一边靠墙围出一块苗圃.
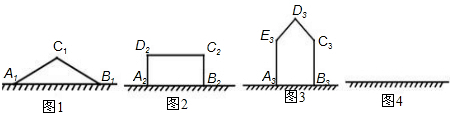
(1)如图1,若围出的苗圃是△A
1B
1C
1,A
1C
1=B
1C
1,靠墙部分A
1B
1=8米;如图2,若围出的苗圃是矩形A
2B
2C
2D
2,靠墙部分A
2B
2=5米.设△A
1B
1C
1的面积为S
1(m
2),矩形A
2B
2C
2D
2的面积为S
2(m
2).试计算S
1与S
2的面积.
(2)如图3,若围出的苗圃是五边形A
3B
3C
3D
3E
3,A
3E
3⊥A
3B
3,B
3C
3⊥A
3B
3,∠C
3=∠E
3=135°,∠D
3=90°.若C
3D
3=D
3E
3=
(m),五边形A
3B
3C
3D
3E
3的面积为S
3(m
2),则它的面积应该为多少?
(3)请你在图4中设计出一种围法,使围成的苗圃的面积大于(1)(2)中苗圃的面积.(说明你所围图形的特征,并计算它的面积)(比较大小时部分参考数据:
≈1.4,
≈1.7,π≈3)
查看答案和解析>>
科目:czsx
来源:
题型:
n个小杯中依次盛有b
1,b
2,…b
n克糖水,并且分别含糖a
1,a
2…,a
n克.
若这n杯糖水的浓度相同,则有连等式
==…=.
现将这n杯糖水合到一个大空杯中,则合杯糖水的浓度与各小杯糖水的浓度还是一样的.
这个尽人皆知的事实,说明一个数学定理----一等比定理:
若
=…=,则
==…=.
若这n杯糖水的浓度互不相同,不妨设
<<…<,
现将这n杯糖水合到一个大空杯中,则合杯糖水的浓度一定大于
,且小于
.
这个尽人皆知的事实,又说明了一个数学定理-----不等比定理:
若
<<…<,则
.

查看答案和解析>>
科目:czsx
来源:
题型:
计算:
(1)(a+b)(a-b)(a4+a2b2+b4);
(2)[(-ab+cd)(cd+ab)(a2b2+c2d2)+2a4b4](c4d4-a4b4).
查看答案和解析>>
科目:czsx
来源:
题型:
已知a+b=2,ab=10,求:
a
3b+a
2b
2+
ab
3的值.
查看答案和解析>>
科目:czsx
来源:
题型:
因式分解:
(1)4a2+6ab+2a;
(2)2x2-12x+18;
(3)3x2-27;
(4)-a2b2+2abc2-c4.
查看答案和解析>>
科目:czsx
来源:
题型:
写出一个只含字母a、b且系数是-1的四次单项式:
-a2b2
-a2b2
.
查看答案和解析>>

 斜拉桥是利用一组组钢索,把桥面重力传递到耸立在两侧高塔上的桥梁,它不需要建造桥墩,(如图所示),B2、B3、B4是B1到高塔底端的四等分点,其中A1B1、A2B2、A3B3、A4B4是斜拉桥上互相平行的钢索,若最长的钢索A1B1=80m,最短的钢索A4B4=20m,那么钢索A2B2=
斜拉桥是利用一组组钢索,把桥面重力传递到耸立在两侧高塔上的桥梁,它不需要建造桥墩,(如图所示),B2、B3、B4是B1到高塔底端的四等分点,其中A1B1、A2B2、A3B3、A4B4是斜拉桥上互相平行的钢索,若最长的钢索A1B1=80m,最短的钢索A4B4=20m,那么钢索A2B2=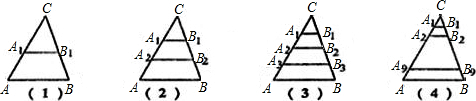
 如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点B1,延长AA1到A2,使A1A2=A1B1,在A2B1上取一点B2,延长到A1A2到A3,使A2A3=A2B2;…按此方法进行下去,∠An-1AnBn-1的度数为
如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点B1,延长AA1到A2,使A1A2=A1B1,在A2B1上取一点B2,延长到A1A2到A3,使A2A3=A2B2;…按此方法进行下去,∠An-1AnBn-1的度数为
 11、挪威数学家阿贝尔,年轻时就利用阶梯形,发现了一个重要的恒等式--阿贝尔公式:如图是一个简单的阶梯形,可用两种方法,每一种把图形分割成为两个矩形.利用它们之间的面积关系,可以得到:a1b1+a2b2=( )
11、挪威数学家阿贝尔,年轻时就利用阶梯形,发现了一个重要的恒等式--阿贝尔公式:如图是一个简单的阶梯形,可用两种方法,每一种把图形分割成为两个矩形.利用它们之间的面积关系,可以得到:a1b1+a2b2=( )
